Teorema della similitudine delle secanti in una circonferenza
Se traccio due secanti da un punto P esterno a una circonferenza, i segmenti su una secante sono gli estremi e quelli sull'altra secante sono i medi di una proporzione, e viceversa.
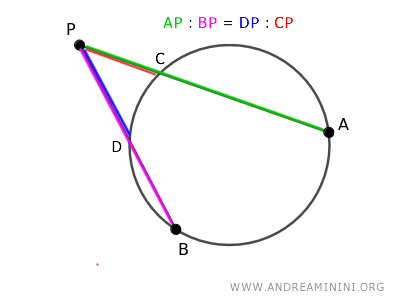
Un esempio pratico
In questo esempio ho una circonferenza e due secanti che hanno origine dallo stesso punto esterno P.
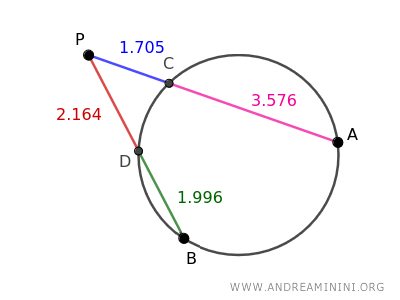
Il segmento AP misura 5.281
$$ \overline{AP} = \overline{AC} + \overline{CP} = 1.705 + 3.576 = 5.281 $$
Il segmento BP misura 4.16
$$ \overline{BP} = \overline{BD} + \overline{DP} = 2.164 + 1.996 = 4.16 $$
Verifico se la proporzione del teorema è soddisfatta
$$ \overline{AP} : \overline{BP} = \overline{DP} : \overline{CP} $$
Sostituisco i valori dei segmenti
$$ 5.281 : 4.16 = 2.164 : 1.705 $$
$$ 1.269 = 1.269 $$
Il teorema è soddisfatto, i segmenti di una secante sono gli estremi della proporzione, quelli dell'altra secante sono i medi.
Nota. Ho approssimato i due quozienti a tre cifre decimali (1.269) perché le misure dei segmenti AP, BP, CP e DP fatte da Geogebra sono misure arrotondate.
La dimostrazione
Considero una circonferenza e un punto esterno P.
Traccio due rette secanti distinte AP e BP.
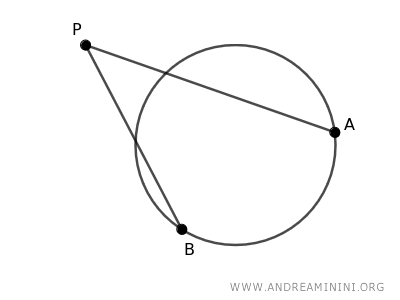
I punti di interesezione C e D delle secanti con la circonferenza dividono le secanti in due segmenti: AC+CP e BD+DP
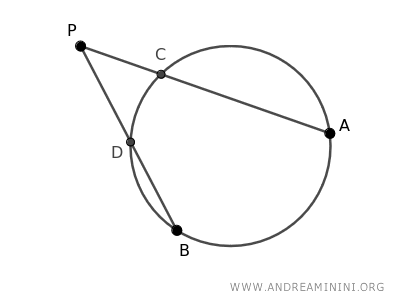
Traccio i segmenti che uniscono l'intersezione di una secante con l'estremo dell'altra secante, ovvero i segmenti AD e BC.
In questo modo si formano due triangoli ADP e BCP.
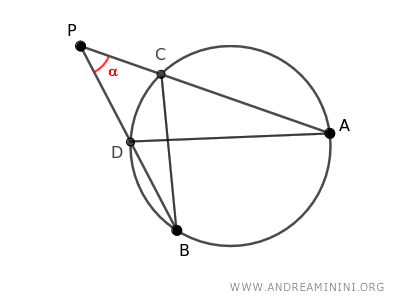
I due triangoli ADP e BCP hanno l'angolo α coincidente.
Gli altri due angoli β e γ sono angoli congruenti β≅γ perché sono due angoli alla circonferenza che insistono sullo stesso arco CD.
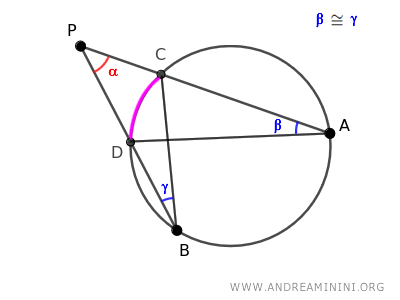
Pertanto, per il primo criterio di similitudine dei triangoli i due triangoli ADP e BCP sono simili, poiché due angoli congruenti α e β≅γ .
$$ ADP \approx BCP $$
Essendo simili hanno i lati omologhi proporzionali.
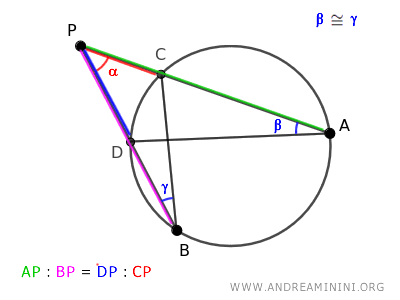
$$ \overline{AP} : \overline{BP} = \overline{DP} : \overline{CP} = \overline{AD} : \overline{BC} $$
Questo conferma la proporzione tra i segmenti:
$$ \overline{AP} : \overline{BP} = \overline{DP} : \overline{CP} $$
E così via.
