Retta tangente di una circonferenza

Una retta è detta retta tangente a una circonferenza quando tocca la circonferenza in un solo punto.

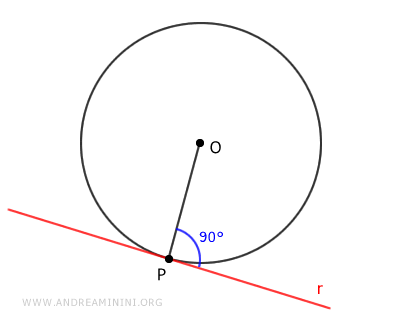
In altre parole, una retta tangente ha un solo punto in comune con la circonferenza.

A differenza delle rette secanti che hanno due punti in comune e delle rette esterne che non ne hanno nessuno.

Nota. In base al teorema dei punti in comune tra una retta e una circonferenza, una retta può intersecare la circonferenza al più in due punti.

L'unicità della retta tangente in punto della circonferenza

In un punto P della circonferenza passa una e una sola retta tangente.

Questo teorema è molto importante perché afferma che in un punto P della circonferenza può esserci una e una sola retta tangente.

Dimostrazione

Considero una circonferenza con centro O e raggio OP. Inoltre, prendo in considerazione una retta (r) tangente alla circonferenza nel punto P.

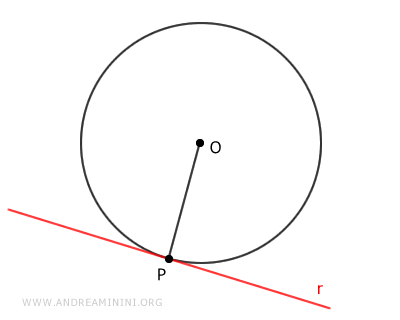
Per definizione, la retta tangente ha un solo punto in comune con la circonferenza.

Sapendo che in un punto di una retta passa un'unica perpendicolare, deduco che la retta tangente abbia una e una sola perpendicolare nel punto P.

In base al teorema della distanza di una retta da una circonferenza, se una retta è tangente in un punto della circonferenza, allora la sua distanza d(r,O) dal centro della circonferenza (O) è uguale al raggio (OP).

$$ d(r,O) \cong \overline{OP} $$

Nota. Quando parlo di "distanza" di una retta (r) da un punto (O) intendo il segmento più corto che li congiunge. Come si può facilmente intuire, qualsiasi altro segmento non perpendicolare alla retta comporta un percorso più lungo per spostarsi dal punto O alla retta r.

 

 

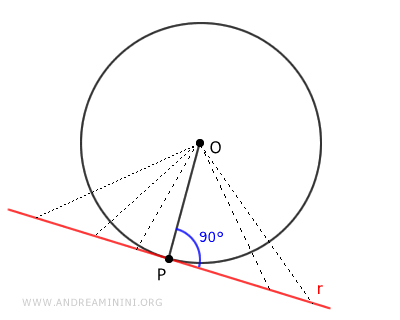
Sapendo che la distanza tra una retta e un punto è sempre perpendicolare alla retta, deduco che anche il raggio è perpendicolare alla retta tangente nel punto P.

$$ \overline{OP} \perp r $$

Poiché nel punto P della retta r non possono esserci altre rette perpendicolari, deduco che nel punto P della circonferenza esiste una e una sola retta tangente.

L'equazione di una retta tangente passante per un punto

In geometria analitica per ottenere l'equazione di una retta tangente che passa per un punto P(x₀;y₀) della circonferenza o esterno, devo costruire un sistema di equazioni composto da due equazioni:

$$ \begin{cases} x^2+y^2+ax+by+c= 0 \\ \\ y-y_0 = m (x-x_0) \end{cases} $$

La prima equazione è l'equazione della circonferenza.

La seconda equazione è l'equazione di una generica retta passante per il punto P(x₀;y₀).

A questo punto ricavo la y nell'equazione della retta e la sostituisco nell'equazione della circonferenza.

$$ \begin{cases} x^2+[m (x-x_0)+y_0]^2+ax+b[m (x-x_0)+y_0]+c= 0 \\ \\ y = m (x-x_0)+y_0 \end{cases} $$

Poi risolvo l'equazione della circonferenza cercando il valore del coefficiente angolare m, ponendo il discriminante Δ=0 come condizione di tangenza.

$$ \Delta = b^2 - 4ac $$

Dove a,b,c sono i coefficienti dell'equazione di 2° grado.

Nota. Il discriminante nullo b²−4ac=0 è detto "condizione di tangenza" perché garantisce che la retta tocchi la circonferenza in un solo punto, confermando che è tangente alla circonferenza. Se non rispettasse questa condizione la retta sarebbe secante o esterna.

Una volta individuata la soluzione "m" possono verificarsi due casi:

• Se il punto P(x₀;y₀) si trova sulla circonferenza, la soluzione del problema è un solo valore del coefficiente angolare m che determina la pendenza dell'unica retta tangente (vedi unicità della retta tangente).
• Se il punto P(x₀;y₀) è esterno alla circonferenza, si hanno due valori m₁ e m₂ del coefficiente angolare perché le rette tangenti alla circonferenza che passano per un punto esterno sono sempre due.

Esempio

Considero una circonferenza definita dalla seguente equazione di 2° grado

$$ x^2+y^2 -6x-4y+9=0 $$

Devo trovare la retta o le rette tangenti (se il punto è esterno alla circonferenza)  che passano per il punto P(9;0).

Al momento non so ancora se il punto si trova sulla circonferenza oppure no.

Costruisco un sistema con un'equazione generica della retta e l'equazione della circonferenza in questione.

$$ \begin{cases} x^2+y^2 -6x-4y+9=0 \\ \\ y-y_0 = m (x-x_0) \end{cases} $$

Sapendo che la retta deve passare nel punto P(9;0) sostituisco le variabili con le coordinate del punto x₀=9 e y₀=0.

$$ \begin{cases} x^2+y^2 -6x-4y+9=0 \\ \\ y-0 = m (x-9) \end{cases} $$

$$ \begin{cases} x^2+y^2 -6x-4y+9=0 \\ \\ y = mx -9m \end{cases} $$

Ricavo y nell'equazione della retta e sostituisco l'espressione nell'equazione della circonferenza

$$ \begin{cases} x^2+(mx -9m)^2 -6x-4(mx -9m)+9=0 \\ \\ y-0 = m (x-9) \end{cases} $$

$$ \begin{cases} x^2+m^2x^2 - 18m^2x + 81m^2 -6x- 4mx+ 36m +9=0 \\ \\ y-0 = m (x-9) \end{cases} $$

Scrivo l'equazione di 2° grado in forma normale.

$$ \begin{cases} x^2 (1 + m^2) + x (- 18m^2-6-4m) + 81m^2 + 36m +9=0 \\ \\ y-0 = m (x-9) \end{cases} $$

Poi impongo la condizione di tangenza ovvero il discriminante nullo nell'equazione di 2° grado.

$$ \Delta = b^2 - 4 ac = 0 $$

In questo caso i coefficienti dell'equazione di 2° grado sono a=1+m², b=-18m²-6-4m, c=81m²+36m+9

$$ \Delta = (-18m^2 - 6 - 4m)^2 - 4(1 + m^2)(81m^2 + 36m + 9) $$

$$ \Delta = (-18m^2 - 6 - 4m) \cdot (-18m^2 - 6 - 4m)  - 4(1 + m^2)(81m^2 + 36m + 9) $$

$$ \Delta = (324m^4 + 144m^3 + 232m^2 + 48m + 36) - 4(81m^4 + 36m^3 + 90m^2+36m+9) $$

$$ \Delta = 324m^4 + 144m^3 + 232m^2 + 48m + 36 - 324m^4 - 144 m^3 - 360m^2 -144 m - 36 $$

$$ \Delta = -128m^2-96m $$

Risolvo l'equazione del discriminante:

$$ \Delta = m \cdot (-128 m - 96) $$

$$ \Delta = 32m \cdot (-4 m -3) $$

Le soluzioni dell'equazione sono:

$$ m = 0 $$

$$ -4m-3= 0 $$

ovvero

$$ m= 0 $$

$$ m = - \frac{3}{4} $$

Quindi i coefficienti angolari delle rette tangenti che passano per il punto P(9;0) sono:

$$ m_1 = 0 $$

$$ m_2 = - \frac{3}{4} $$

A questo punto trovo le equazioni delle rette tangenti.

Per \(m = 0\):

$$ y = 0 $$

Per \(m =  - \frac{3}{4}\):

$$ y = - \frac{3}{4}(x - 9) $$

$$ y = - \frac{3}{4}x + \frac{3 \cdot 9}{4} $$

$$ y = - \frac{3}{4}x + \frac{27}{4} $$

Le equazioni delle rette tangenti sono quindi:

$$ y = 0 $$

$$ y = - \frac{3}{4}x + \frac{27}{4} $$

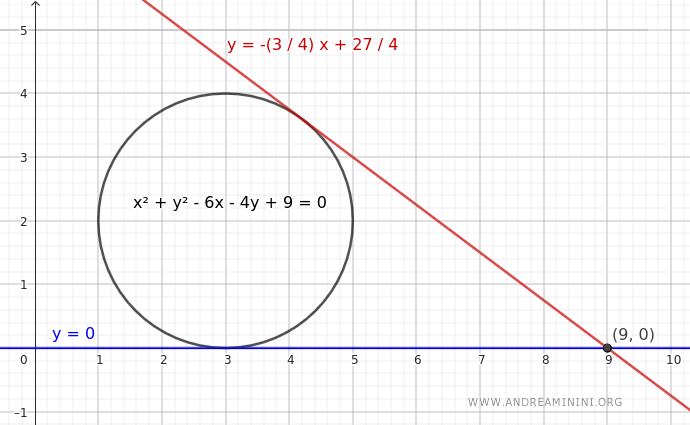
Queste sono le rette tangenti alla circonferenza passanti per il punto \(P(9, 0)\).

Altri metodi per determinare le equazioni delle rette tangenti

Ecco altri metodi per ottenere l'equazione delle rette tangenti alla circonferenza.

• Metodo della distanza tra la retta e il centro della circonferenza
• Metodo della retta tangente perpendicolare al raggio
• Il metodo delle formule di sdoppiamento

Metodo della distanza tra la retta e il centro della circonferenza

Questo metodo si basa sulle coordinate del centro C della circonferenza e sulla lunghezza del raggio r.

Scrivo l'equazione del fascio di rette che passa per il punto P(x₀;y₀) che può essere un punto della circonferenza o anche un punto esterno qualsiasi.

$$ y - y_0 = m(x-x_0) $$

Poi cerco tra le rette del fascio quella che ha la distanza dal centro della circonferenza C(x_c;y_c) uguale al raggio r e da queste ricavo il coefficiente angolare m.

$$ d = \frac{|ax_c+by_c+c|}{ \sqrt{a^2+b^2}} = r $$

Le rette che soddisfano questa distanza sono tangenti alla circonferenza.

Esempio

Considero il punto P(9;0) e la circonferenza seguente:

$$ x^2+y^2 -6x-4y+9=0 $$

A questo punto trovo calcolo le coordinate del centro della circonferenza, sapendo che a=-6 e b=-4

$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$

$$ (x_0, y_0) = \left(-\frac{-6}{2}, -\frac{-4}{2}\right) $$

$$ (x_0, y_0) = \left( 3, 2 \right) $$

Il raggio r lo determino mediante quest'altra formula, sapendo che a=-6, b=-4 e c=9

$$ r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c} $$

$$ r = \sqrt{\left(-\frac{-6}{2}\right)^2 + \left(-\frac{-2}{2}\right)^2 - 9} $$

$$ r = \sqrt{3^2 +2^2 - 9} $$

$$ r = \sqrt{9 +4 - 9} $$

$$ r = \sqrt{4} $$

$$ r = 2 $$

Quindi, il centro della circonferenza si trova alle coordinate C(3;2) mentre il raggio è lungo r=2.

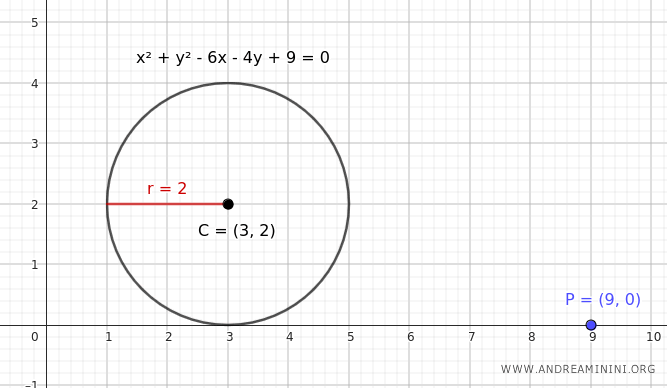
A questo punto scrivo l'equazione del fascio di rette che passa nel punto P(x₀;y₀)=(9;0)

$$ y - y_0 = m(x-x_0) $$

$$ y - 0 = m(x-9) $$

$$ y  = mx-9m $$

Scrivo l'equazione del fascio di rette in forma normale ovvero ax+by+c=0 , in questo caso a=m, b=-1, c=-9m

$$ mx- y -9m = 0 $$

Cerco le rette che hanno una distanza dal centro della circonferenza C(3;2) uguale al raggio r=2, sapendo che le coordinate del punto C(3;2) sono x_c=3 e y_c=2 mentre i coefficienti del fascio di rette sono a=m, b=-1, c=-9m.

$$ d = \frac{|ax_c+by_c+c|}{ \sqrt{a^2+b^2}} = r $$

$$ \frac{|m \cdot (3)-1 \cdot (2) - 9m|}{ \sqrt{m^2+(-1)^2}} = 2 $$

$$ \frac{|3m-2- 9m|}{ \sqrt{m^2+1}} = 2 $$

$$  \frac{|-6m-2|}{ \sqrt{m^2+1}} = 2 $$

$$ |-6m-2| = 2 \cdot \sqrt(m^2+1) $$

Elevo entrambi i membri al quadrato

$$ ( |-6m-2| )^2 = (2 \cdot \sqrt(m^2+1) )^2 $$

$$ (6m+2)^2 = 4 \cdot (m^2+1) $$

$$ 36m^2 + 24m + 4= 4m^2 + 4 $$

$$ 36m^2 + 24m + 4- 4m^2 - 4 = 0 $$

$$ 32m^2 + 24m = 0 $$

A questo punto risolvo l'equazione per trovare m (il coefficiente angolare delle rette).

In questo caso fattorizzo per m anziché risolvere l'equazione di 2° grado

$$ m \cdot (32m+24) = 0 $$

La prima soluzione è banale m=0.

$$ m_1 = 0 $$

La seconda soluzione la ottengo risolvendo 32m+24=0 ed è m=-3/4

$$ m_2 = - \frac{24}{32}  = - \frac{3}{3} $$

Infine, riprendo l'equazione del fascio di rette e utilizzo i due coefficienti angolari m₁=0 e m₂=-3/4 che ho appena trovato.

$$ y  = mx-9m $$

Con m₁=0 ottengo l'equazione di una retta tangente y=0

$$ y  = mx-9m = 0 \cdot x-9 \cdot 0 = 0 $$

Con m₂=-3/4 ottengo l'equazione di un'altra retta tangente y=-(3/4)x+27/4

$$ y  = mx-9m = -\frac{3}{4} \cdot x-9 \cdot ( - \frac{3}{4} ) = - \frac{3}{4}x + \frac{27}{4} $$

In questo esempio, essendo P(9;0) un punto esterno alla circonferenza, ci sono due rette tangenti alla circonferenza che passano per il punto P.

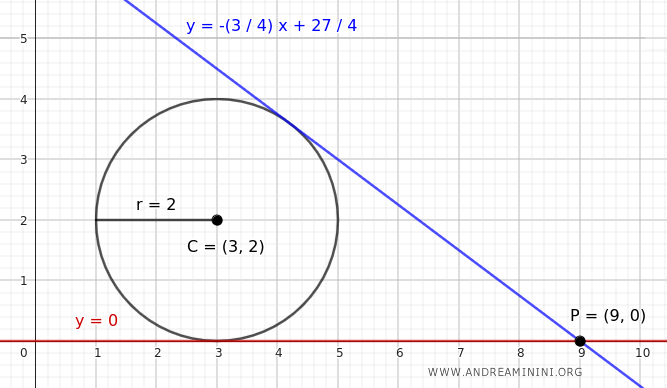
Metodo della retta tangente perpendicolare al raggio

Questo metodo si basa sul fatto che una retta tangente in un punto P della circonferenza è sempre perpendicolare al raggio, secondo il teorema della perpendicolarità tra raggio e tangente.

Sapendo che, quando due rette sono perpendicolari il prodotto dei loro coefficienti angolari è uguale a -1.

$$ m_r \cdot m_t = -1 $$

Pertanto, c'è una relazione tra i due coefficienti

$$ m_t = - \frac{1}{m_r} $$

Una volta calcolata l'equazione della retta a cui appartiene il raggio $ y = m_r x + q $ è molto facile trovare anche quella della retta tangente.

Basta applicare il reciproco opposto del coefficiente angolare all'equazione che rappresenta il fascio di rette che passa per il punto di tangenza P(x₀;y₀).

$$ y-y_0 = m_t \cdot (x-x_0) $$

Nota. Questo metodo si applica solo se il punto P si trova sulla circonferenza. Non si applica se è un punto esterno.

Esempio

Considero una circonferenza di cui conosco l'equazione:

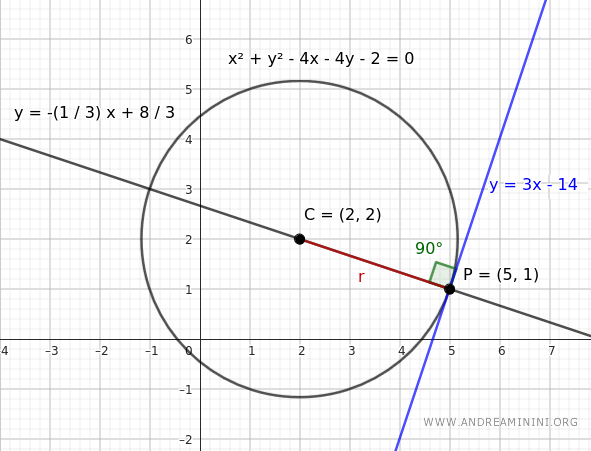
$$ x^2+y^2-4x-4y-2=0 $$

Voglio trovare la retta tangente nel punto P(5,1) della circonferenza.

$$ P(5,1) $$

Per prima cosa, calcolo il centro della circonferenza, sapendo che nell'equazione della circonferenza a=-4 e b=-4

$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$

$$ (x_0, y_0) = \left(-\frac{-4}{2}, -\frac{-4}{2}\right) $$

$$ (x_0, y_0) = \left( 2, 2 \right) $$

Il centro C della circonferenza si trova alle coordinate (x,y)=(2,2)

$$ C(2,2) $$

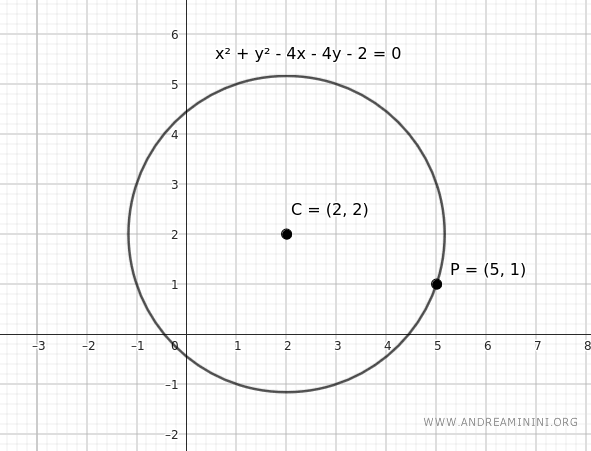
Una volta noto il centro della circonferenza C(2,2) e il punto di tangenza P(5,1), trovo l'equazione della retta che passa per i due punti, ovvero la retta a cui appartiene il raggio della circonferenza.

$$  \frac{y-y_c}{y_t-y_c}= \frac{x-x_c}{x_t-x_c} $$

Le coordinate del centro C della circonferenza sono (x_c,y_c)=(2,2) mentre quelle del punto di tangenza P sono (x_t,y_t)=(5,1)

$$  \frac{y-2}{1-2}= \frac{x-2}{5-2} $$

$$  \frac{y-2}{-1}= \frac{x-2}{3} $$

$$  y-2= - \frac{x-2}{3} $$

$$  y= - \frac{x-2}{3} +2 $$

$$  y= - \frac{x}{3} + \frac{2}{3} +2 $$

$$  y= - \frac{x}{3} + \frac{2+6}{3} $$

$$  y= - \frac{1}{3} \cdot x + \frac{8}{3} $$

Quindi, il coefficiente angolare dell'equazione a cui appartiene il raggio è m_r=-1/3

$$ m_r = - \frac{1}{3} $$

Sapendo che la retta tangente nel punto P è perpendicolare al raggio e che il prodotto dei coefficienti angolari di due rette perpendicolari è m_rm_t=.1, deduco che il coefficiente angolare della retta tangente è m_t=3.

$$ m_t = - \frac{1}{m_r} $$

$$ m_t = - \frac{1}{ - \frac{1}{3} } $$

$$ m_t = 3 $$

Ora resta solo da capire qual'è l'equazione della retta tangente al punto P(5,1).

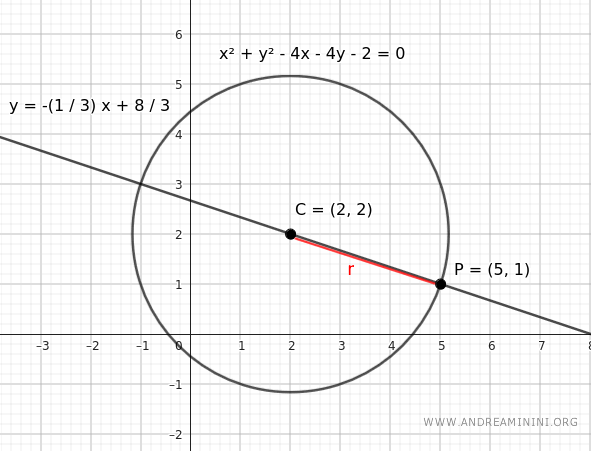
Per trovarla utilizzo l'equazione del fascio di rette che passa per un punto.

$$ y-y_0 = m \cdot (x-x_0) $$

Sostituisco le coordinate (x0,y0) con quelle del punto P(5,1) ovvero x₀=5 e y₀=1.

$$ y-1 = m \cdot (x-5) $$

Poiché il coefficente che mi interessa è m_t=3, l'equazione della retta tangente al punto P è la seguente:

$$ y-1 = 3 \cdot (x-5) $$

$$ y = 3 x-15 + 1 $$

$$ y = 3 x-14 $$

Ho trovato l'equazione della retta tangente al punto P.

Il metodo delle formule di sdoppiamento

Per ottenere l'equazione di una retta tangente a un punto P(x₀;y₀₎ della circonferenza posso usare anche la formula di sdoppiamento

$$ xx_0 + yy_0 + a \frac{x+x_0}{2} + b \frac{y+y_0}{2} + c = 0 $$

Questa formula restituisce direttamente l'equazione della retta tangente.

Tuttavia, si può applicare solo se P è un punto della circonferenza, non si applica se P è un punto esterno.

Esempio

Considero la stessa circonferenza dell'esempio precedente

$$ x^2+y^2-4x-4y-2=0 $$

Devo trovare l'equazione della retta tangente al punto P(5,1) della circonferenza.

$$ P(5,1) $$

In questo caso utilizzo la formula di soppiamento.

$$ xx_0 + yy_0 + a \frac{x+x_0}{2} + b \frac{y+y0}{2} + c = 0$$

$$ xx_0 + yy_0 + \frac{a}{2}(x + x_0) + \frac{b}{2}(y + y_0) + c = 0 $$

Per la circonferenza \( x^2 + y^2 - 4x - 4y - 2 = 0 \) ho questi coefficienti:

 \( a = -4 \)
 \( b = -4 \)
 \( c = -2 \)

Sostituisco i coefficienti a=-4, b=-4 e c=-2 dell'equazione della circonferenza nella formula di sdoppiamento.

$$ xx_0 + yy_0 + \frac{-4}{2}(x + x_0) + \frac{-4}{2}(y + y_0) - 2 = 0 $$

Le coordinate del punto di tangenza P(5,1) sono x₀=5 e y₀=1.

$$ x \cdot 5 + y \cdot 1 + \frac{-4}{2}(x + 5) + \frac{-4}{2}(y + 1) - 2 = 0 $$

$$ 5x + y - 2(x + 5) - 2(y + 1) - 2 = 0 $$

$$ 5x + y - 2x - 10 - 2y - 2 - 2 = 0 $$

$$ 3x - y - 14 = 0 $$

Quindi, l'equazione corretta della retta tangente è:

$$ 3x - y - 14 = 0 $$

Ho trovato l'equazione generale della retta tangente.

A questo punto, se voglio conoscere il coefficiente angolare mi basta ricavare la y

$$ y = 3x - y - 14  $$

Il coefficiente angolare della retta tangente è m=3.

E così via.