L'area di un poligono regolare

L'area di un poligono regolare si ottiene moltiplicando il semiperimetro (p) per l'apotema (a) $$ A = p \cdot a $$ Dove l'apotema è la distanza di ogni lato dal centro mentre il semiperimetro è la metà del perimetro 2p=P quindi p=P/2.

La spiegazione

L'idea sta nel fatto di suddividere un poligono regolare in tanti triangoli congruenti che hanno un vertice al centro del poligono e come base un lato del poligono.

Ad esempio, un esagono si può scomporre in 6 triangoli congruenti.

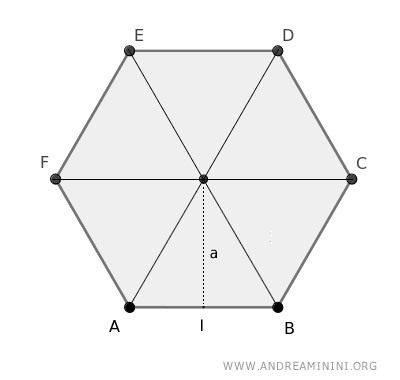
L'area di ogni triangolo si ottiene con la classica formula: lato (l) per altezza (h) diviso due.

$$ \frac{l \cdot h}{2} $$

Nel caso dei poligoni, l'altezza dei triangoli coincide con l'apotema (a) ossia con la distanza tra ogni lato e il centro del poligono.

Quindi, posso riscrivere la formula dell'area di un triangolo in questo modo:

$$ \frac{l \cdot a}{2} $$

Una volta trovata l'area di un triangolo, la moltiplico per il numero dei triangoli, ossia dei lati del poligono, trovando così l'area del poligono.

$$ A = n \cdot \frac{l \cdot a}{2} $$

Ad esempio, per trovare l'area dell'esagono mi basta calcolare l'area di un triangolo e moltiplicarlo per 6. $$ A = 6 \cdot \frac{l \cdot a}{2} $$

 

Sapendo che il perimetro di un poligono regolare è il prodotto P=n·l tra la lunghezza di un singolo lato (l) e il numero dei lati (n), posso riscrivere la formula precedente in questa forma più compatta

$$ A = \frac{P \cdot a}{2} $$

La lettera P maiuscola indica il perimetro del poligono.

Poiché in geometria con la "p" minuscola si indica il semiperimetro p=P/2 ossia la metà del perimetro (P), posso ulteriormente semplificare la formula dell'area scrivendola nel modo seguente:

$$ A = p \cdot a $$

In questo modo la formula diventa molto più semplice da ricordare.

In conclusione, questo dimostra che l'area di un poligono regolare è uguale al prodotto tra il semiperimetro (p) e l'apotema (a).

Un esempio pratico

Ho un esagono regolare in cui ogni lato è lungo l=6 e l'apotema è a=5,2.

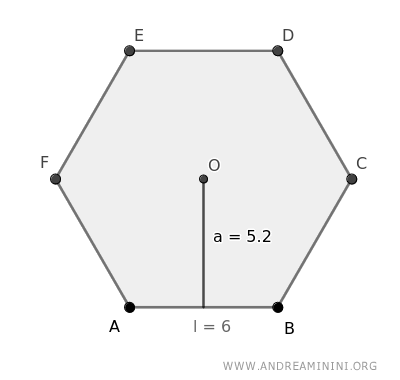
Calcolo il perimetro (P) sapendo che l'esagono ha sei lati.

$$ P = 6 \cdot 6 = 36 $$

Poi, lo divido a metà per ottenere il semiperimetro (p)

$$ p = \frac{P}{2} = \frac{36}{2} = 18 $$

Infine, moltiplico il semiperimetro (p=18) per l'apotema (a=5,2) per ottenere l'area dell'esagono (A)

$$ A = p \cdot a = 18 \cdot 5,2 = 93,6 $$

L'area dell'esagono è 93,6

Nota. In alternativa avrei potuto calcolare l'area di un singolo triangolo usando la formula base (l) per altezza (h) diviso due, sapendo che il lato è l=6 e l'altezza coincide con l'apotema h=a=5,2 $$ A_t = \frac{l \cdot h}{2} = \frac{6 \cdot 5,2}{2} = \frac{31,2}{2} = 15,6 $$ Una volta ottenuta l'area di un triangolo (A_t=15,6) mi basta moltiplicarla per il numero di triangoli in cui ho suddiviso l'esagono. In questo caso i triangoli sono n=6 $$ A = A_t \cdot n = 15,6 \cdot 6 = 93,6 $$ Il risultato finale è l'area dell'esagono.

Questa formula funziona per tutti i poligoni regolari, non solo per l'esagono.

Che si tratti di un pentagono, un ottagono o un decagono, la formula rimane la stessa.

Esempio 2

Considero un pentagono con i lati lunghi l=2,5 e un apotema a=1,72

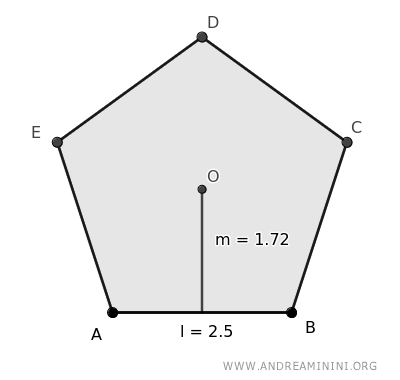
Nota. Nella geometria piana il pentagono può essere suddiviso in cinque triangoli.

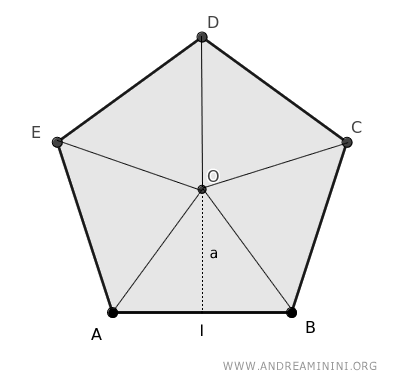
Calcolo il perimetro (P) del pentagono sapendo che ha n=5 lati e ogni lato è lungo l=2,5

$$ P = n \cdot l = 5 \cdot 2,5 = 12,5 $$

Poi calcolo il semiperimetro (p) sapendo che 2p=P=12.5

$$ p = \frac{p}{2} = \frac{12,5}{2} = 6,25 $$

Infine, trovo l'area del pentagono (A) moltiplicando il semiperimetro p=6,25 per l'apotema a=1,72

$$ A = p \cdot a = 6,25 \cdot 1,72 = 10,75 $$

Quindi, l'area del pentagono è A=10,75

Osservazioni e note

Alcune osservazioni e note aggiuntive

• Le formule inverse
  Dalla formula diretta $$ A=p \cdot a $$ si ottengono le formule inverse per calcolare il semiperimetro nota l'area e l'apotema, oppure l'apotema nota l'area e il semiperimetro $$ p = \frac{A}{a} $$ $$ a = \frac{A}{p} $$ Sapendo che il perimetro è il doppio del semiperimetro P=2p $$ P = 2p = \frac{2A}{a} $$
• L'apotema è sempre perpendicolare al lato del poligono
  In un poligono regolare, l'apotema è anche il raggio della circonferenza inscritta. Questo può essere utile quando conosco il raggio della circonferenza inscritta nel poligono ma non l'apotema.
• Poligoni con un grande numero di lati
  Man mano che il numero di lati di un poligono regolare aumenta, il poligono tende a diventare un cerchio. In questo caso, l'apotema tende a diventare il raggio del cerchio.
• Relazione tra apotema, raggio e angoli
  L'apotema, il raggio e gli angoli interni di un poligono regolare sono collegati tra loro. Ad esempio, in un esagono regolare, l'angolo al centro è di 60° (360°/6). Usando le funzioni trigonometriche, si può trovare l'apotema conoscendo il raggio, e viceversa.
• Equivalenza tra un poligono regolare e un triangolo
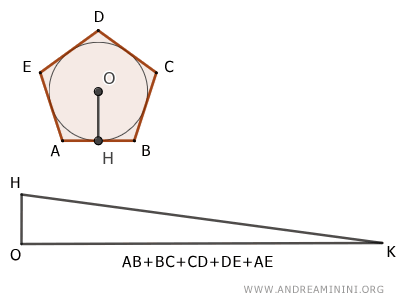
  L'area di un poligono regolare è uguale a quella di un triangolo che ha per base il perimetro del poligono regolare e per altezza l'apotema del poligono regolare.
  

E così via