L'equazione della circonferenza

L'equazione standard di una circonferenza nel piano cartesiano è data da: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$ dove \((x_0, y_0)\) rappresenta le coordinate del centro \(O\) della circonferenza e \(r\) è il raggio.

Alternativamente, posso scrivere l'equazione della circonferenza anche nella forma generale:

$$ x^2 + y^2 + ax + by + c = 0 $$

I coefficienti sono legati al centro e al raggio della circonferenza tramite le relazioni:

$$ a = -2x_0 $$

$$ b = -2y_0 $$

$$ c = x_0^2 + y_0^2 - r^2 $$

Per calcolare le coordinate del centro \(O\) a partire dalla forma generale, utilizzo la formula del centro della circonferenza:

$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$

Il raggio \(r\) si determina mediante la formula del raggio che si basa sulla distanza euclidea tra il centro e un punto della circonferenza:

$$ r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c} $$

È importante notare che la condizione perché \(x^2 + y^2 + ax + by + c = 0\) descriva effettivamente una circonferenza è che:

$$ \left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c \geq 0 $$

Questa condizione assicura che il valore sotto radice quadrata sia non negativo, dato che il raggio \(r\), essendo una lunghezza, non può essere negativo.

Inoltre, è possibile esprimere l'equazione della circonferenza in forma esplicita rispetto a \(y\):

$$ y = y_0 \pm \sqrt{r^2 - (x - x_0)^2} $$

Questo  evidenzia che per certi valori di \(x\) esistono due corrispondenti valori di \(y\) (superiore e inferiore), a meno che il termine sotto radice non sia zero, caso in cui la circonferenza si riduce a un punto (circonferenza degenere, quando \(r = 0\)).

Un esempio pratico

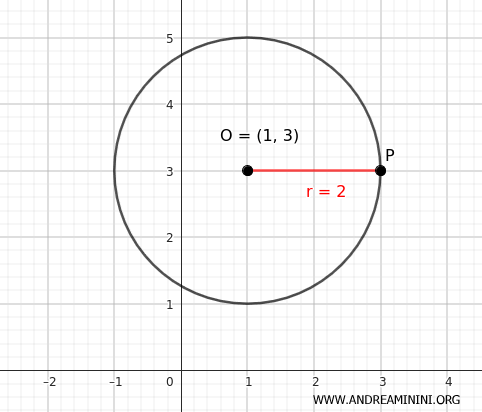
Considero la costruzione di una circonferenza con centro nel punto \( (x, y) = (1, 3) \) e raggio \( r = 2 \).

L'equazione canonica di una circonferenza che soddisfa queste caratteristiche è data dalla formula:

$$  (x - x_0)^2 + (y - y_0)^2 = r^2 $$

Sostituendo i valori di x₀=1, y₀=3, r=2 ottengo:

$$  (x - 1)^2 + (y - 3)^2 = 2^2 $$

$$ (x - 1)^2 + (y - 3)^2 = 4 $$

Questa equazione rappresenta l'insieme di tutti i punti nel piano che distano esattamente 4 unità dal centro \( (1, 3) \), formando una circonferenza.

La dimostrazione

Considero una circonferenza di raggio "r" e centro O(x₀;y₀).

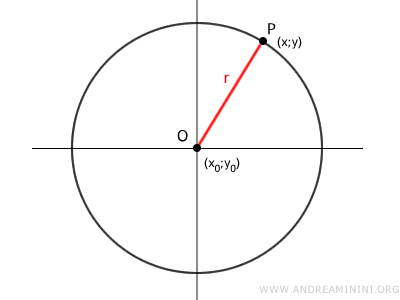
Un generico punto P(x;y) del piano appartiene alla circonferenza se e solo se dista dal centro O una lunghezza pari al raggio r della circonferenza.

$$ \overline{OP} = r $$

Elevo al quadrato entrambi i membri dell'equazione

$$ \overline{OP}^2 = r^2 $$

La lunghezza del segmento OP è uguale alla distanza tra i punti O e P che si misura usando il teorema di Pitagora.

$$ \overline{OP} = \sqrt{ (x-x_0)^2 + (y-y_0)^2 } $$

Quindi, posso riscrivere l'equazione in questa forma equivalente

$$ \overline{OP}^2 = r^2 $$

$$ ( \sqrt{ (x-x_0)^2 + (y-y_0)^2 } )^2 = r^2 $$

Il risultato finale è l'equazione in forma standard della circonferenza.

$$ (x-x_0)^2 + (y-y_0)^2 = r^2 $$

A questo punto, per ottenere anche l'altra formula svolgo i due quadrati

$$ x^2+x_0^2-2xx_0 + y^2+y_0^2-2yy_0 = r^2 $$

$$ x^2+ y^2-2xx_0 -2yy_0+x_0^2 +y_0^2 - r^2 = 0 $$

Considero a=-2x₀, b=-2y₀, c=x₀²+y₀²-r²

$$ x^2+ y^2-2x_0 \cdot x - 2y_0 \cdot y+( x_0^2 + y_0^2 - r^2 ) = 0 $$

$$ x^2+ y^2+ a \cdot x +b \cdot y+ c = 0 $$

Il risultato finale è l'equazione generale della circonferenza.

$$ x^2+ y^2+ ax +by+ c = 0 $$

Sapendo che a=-2x₀ e b=-2y₀ , ricavo le coordinate x₀=-a/2 e y₀=-b/2

Quindi, le coordinate (x_0; y₀) del centro della circonferenza sono

$$ (x_0 ; y_0) = ( - \frac{a}{2} ; - \frac{b}{2} ) $$

Per ottenere la formula del raggio confronto le due equazioni della circonferenza \( x^2+x_0^2+ \frac{a}{2} x + \frac{b}{2}y + y^2+y_0^2 - r^2 = 0 \) con quelli dell'equazione \( x^2+ y^2+ ax +by+ c = 0 \)

• Equazione standard della circonferenza
  $$ x^2+x_0^2+ \frac{a}{2} x + \frac{b}{2}y + y^2+y_0^2 - r^2 = 0 $$
• Equazione generale della circonferenza
  $$ x^2+ y^2+ ax +by+ c = 0 $$

I termini costanti nelle due equazioni sono r², x₀² e y₀² nella prima equazione e c nella seconda equazione

Nota. Dove per "termine costante" intendo quei termini che non sono moltiplicati per una variabile, quindi sono costanti perché il loro valore non cambia a prescindere dai valori delle variabili x e y dell'equazione.

Essendo costanti, questi termini devono essere uguali in entrambe le equazioni.

In altre parole, la somma dei termini costanti della prima equazione x₀²+y₀²-r² è uguale al termine "c" della seconda equazione della circonferenza.

Quindi, comparo ed eguaglio i termini costanti delle due equazioni.

$$ x_0^2 + y_0^2 - r^2 = c $$

In questo modo posso ricavare il raggio r della circonferenza

$$ r^2 = x_0^2 + y_0^2 - c $$

$$ \sqrt{ r^2 } = \sqrt{ x_0^2 + y_0^2 - c } $$

$$ r = \sqrt{ x_0^2 + y_0^2 - c } $$

Sapendo che a=-2x₀, b=-2y₀, ricavo le coordinate x₀=-a/2 e y₀=-b/2

$$ r = \sqrt{ ( - \frac{a}{2} )^2 + ( - \frac{b}{2} )^2 - c } $$

E' la formula del raggio che volevo ottenere

Studio dei casi per l'equazione della circonferenza

L'equazione generale della circonferenza nel piano cartesiano è data da:

$$ x^2 + y^2 + ax + by + c = 0 $$

Dove i coefficienti \( a \), \( b \) e \( c \) sono numeri reali che determinano la posizione della circonferenza nel piano. Di seguito sono riportati i principali casi particolari:

• Centro della circonferenza nell'origine
  Per costruire una circonferenza che ha come centro l'origine degli assi cartesiani, basta porre a zero i coefficienti \( a \) e \( b \): \[ x^2 + y^2 + c = 0 \]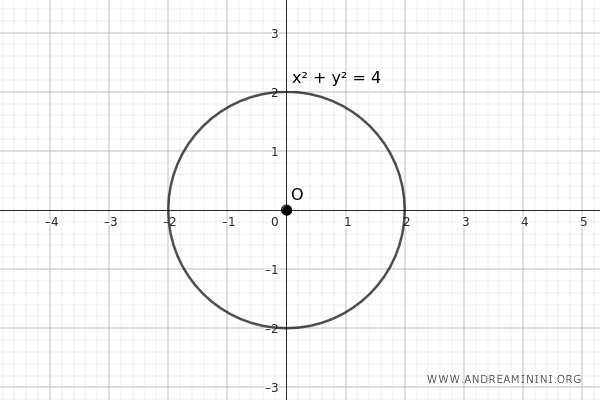
• Centro della circonferenza sull'asse \( x \)
  Una circonferenza che ha il centro sull'asse delle ascisse (asse \( x \)) ha il coefficiente \( b \) uguale a zero: \[ x^2 + y^2 + ax + c = 0 \]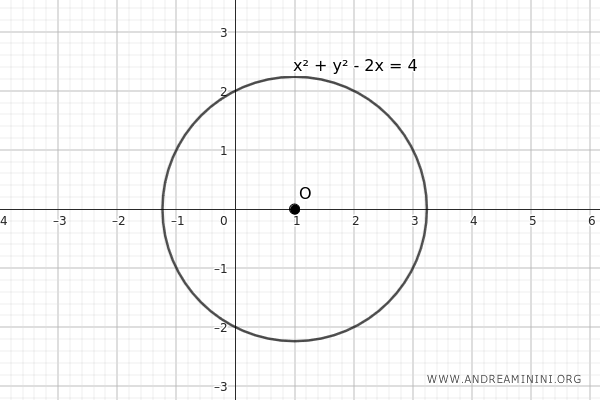
• Centro della circonferenza sull'asse \( y \)
  Una circonferenza che ha il centro sull'asse delle ordinate (asse \( y \)) ha il coefficiente \( a \) uguale a zero: \[ x^2 + y^2 + by + c = 0 \]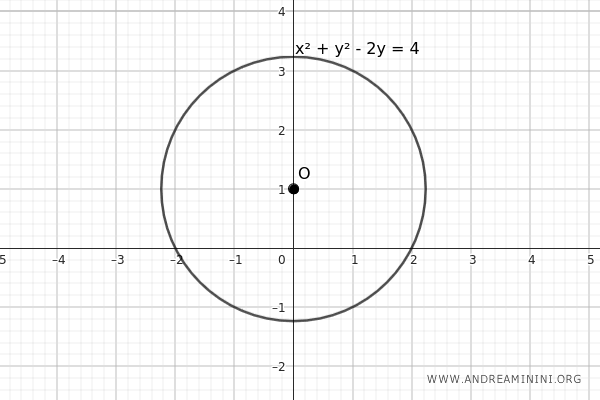
• Circonferenza che passa per l'origine degli assi
  Una circonferenza passa per l'origine degli assi cartesiani quando ha il coefficiente \( c \) uguale a zero: \[ x^2 + y^2 + ax + by = 0 \]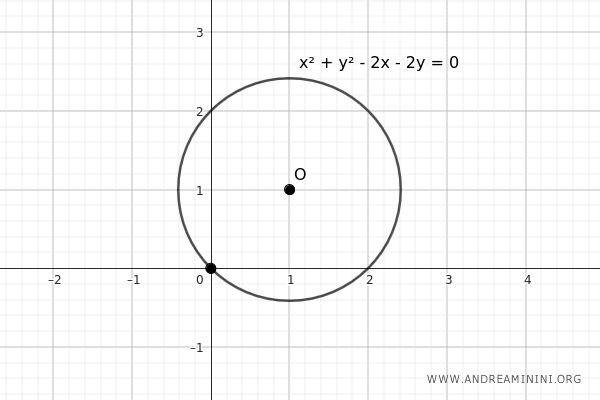

Nota. Combinando questi casi si possono ottenere altre configurazioni. Ad esempio, per avere una circonferenza che ha il centro sull'asse delle ascisse (\( b = 0 \)) e che passa per l'origine degli assi cartesiani (\( c = 0 \)), basta combinare le due condizioni: $$ x^2 + y^2 + ax = 0 $$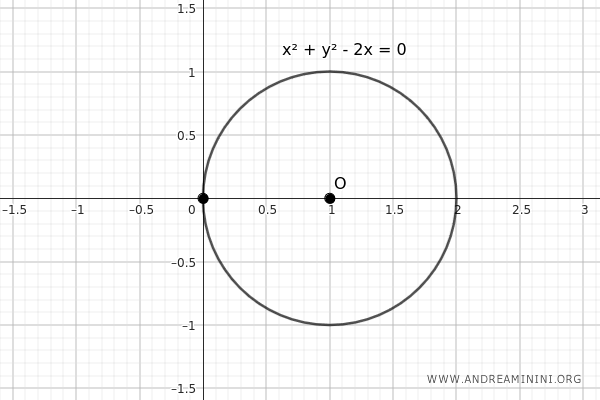

Osservazioni

Alcune osservazioni e note a margine sull'equazione della circonferenza

• Come ottenere l'equazione della conoscenza conoscendo il centro e il raggio
  Sapendo che la distanza da ogni punto della circonferenza è costante ed è pari al raggio, noto il centro C(x₀,y₀) e il raggio r posso ottenere l'equazione della circonferenza tramite questa formula. $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
• L'equazione della circonferenza dato il diametro
  Per trovare l'equazione della circonferenza conoscendo gli estremi A e B di un diametro, posso ricavare il centro tramite il punto medio del segmento AB $$ C \left( \frac{x_A+x_B}{2} ; \frac{y_A+y_B}{2} \right) $$ e il raggio dalla metà della distanza tra i punti A e B. $$ r = \frac{1}{2}  \cdot \sqrt{(x_A-x_B)^2+(y_A-y_B)^2} $$ Una volta noti raggio e centro applico la formula $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
• L'equazione della circonferenza che passa per tre punti non allineati
  Dati tre punti non allineati A(x₁,y₁), B(x₂,y₂), C(x₃,y₃), l'equazione della circonferenza che passa per i tre punti si ottiene trovando le soluzioni "a", "b" e "c" del sistema di equazioni $$ \begin{cases} x^2_1+y^2_1+ax_1+by_1 + c = 0 \\ x^2_2+y^2_2+ax_2+by_2 + c = 0 \\ x^2_3+y^2_3+ax_3+by_3 + c = 0 \end{cases} $$ Una volta trovati i coefficienti "a", "b", "c", li sostituisco nell'equazione generale della circonferenza $$x^2 + y^2 + ax + by + c = 0 $$
  

E così via.