Teorema dei punti in comune tra una retta e una circonferenza
Una retta e una circonferenza possono intersecarsi al massimo in due punti.
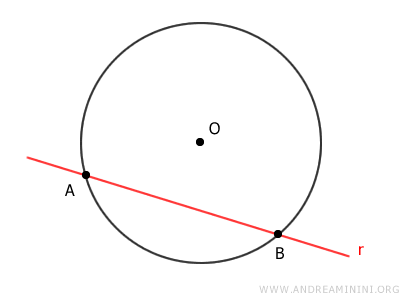
In altre parole, una retta e una circonferenza che si intersecano, posso avere al massimo due punti in comune.
Se la retta interseca la circonferenza in due punti, è detta retta secante alla circonferenza.

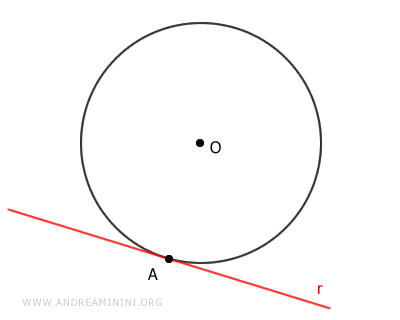
Se la retta ha un solo punto in comune con la circonferenza, è detta retta tangente alla circonferenza.
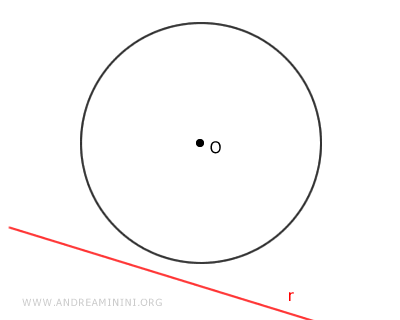
Infine, se la retta non ha nessun punto in comune con la circonferenza, è detta retta esterna alla circonferenza.
La dimostrazione
Per dimostrarlo faccio un ragionamento per assurdo.
Ipotizzo che la retta r e la circonferenza abbiamo tre o più punti in comune: A, B, C
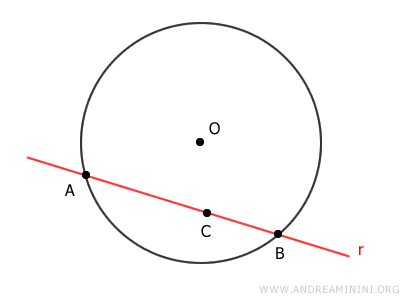
I tre punti appartengono alla stessa retta r, quindi formano dei segmenti AB e BC allineati.
Essendo segmenti allineati, AB e BC hanno i propri assi perpendicolari alla retta r e paralleli tra loro.
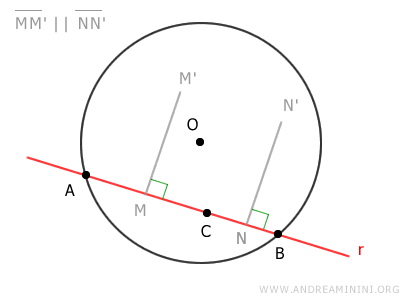
Gli assi MM' e NN' dei segmenti AB e BC sono paralleli, quindi non si intersecano tra loro
$$ \overline{MM'} \cap \overline{NN'} = Ø $$
Tuttavia, i segmenti AB e BC sono anche corde della circonferenza, perché per ipotesi i punti A, B, C sono punti di intersezione che appartengono anche alla circonferenza oltre che alla retta.
Sapendo che l'asse di qualsiasi corda passa per il centro del cerchio, deduco che l'asse delle corde AB e BC passi per il punto O.
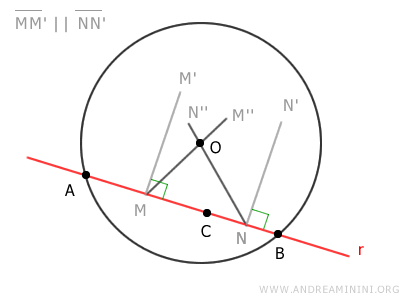
Pertanto, gli assi MM' e NN' dei segmenti AB e BC hanno in comune il punto O, quindi si intersecano tra loro.
$$ \overline{MM'} \cap \overline{NN'} = O $$
Questo però è impossibile perché i segmenti AB e BC risulterebbero contemporaneamente paralleli e incidenti.
$$ \overline{MM'} \cap \overline{NN'} = Ø $$
$$ \overline{MM'} \cap \overline{NN'} = O $$
Questo dimostra che la retta e la circonferenza non possono avere tre punti in comune.
Nota. Lo stesso ragionamento si ripete tale e quale se ipotizzo che esistano quattro o più punti in comune tra la retta e la circonferenza.
Se l'ipotesi iniziale è falsa, vuol dire che è vero il suo contrario.
Pertanto, una retta e una circonferenza possono intersecarsi al più in due punti.
E così via.
