La formula per trovare il centro di una circonferenza
Per trovare le coordinate (x;y) del centro di una circonferenza con l'equazione scritta nella forma generale $$ x^2 + y^2 + Dx + Ey + F = 0 $$ posso utilizzare questa formula $$ O(x,y) = ( -\frac{D}{2}, -\frac{E}{2} ) $$
Quando l'equazione della circonferenza è scritta nella forma standard
\[ (x - h)^2 + (y - k)^2 = r^2 \]
Il centro e il raggio della circonferenza sul piano cartesiano sono molto più evidenti
- \( (h, k) \) sono le coordinate del centro della circonferenza
- \( r \) è il raggio della circonferenza.
Se invece ho l'equazione generale della circonferenza nella forma:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
Posso trovare il centro \((h, k)\) usando le seguenti formule:
$$ h = -\frac{D}{2} $$
$$ k = -\frac{E}{2} $$
In queste formule, \(D\) ed \(E\) sono i coefficienti delle variabili \(x\) e \(y\) nell'equazione generale $ x^2 + y^2 + Dx + Ey + F = 0 $ della circonferenza.
Quindi, il centro della circonferenza è dato dalle coordinate \((-D/2, -E/2)\).
Nota. In alternativa, posso trovare le coordinate del centro trasformando l'equazione generale della circonferenza $ x^2 + y^2 + Dx + Ey + F = 0 $ nell'equazione standard $ (x - h)^2 + (y - k)^2 = r^2 $ completando i quadrati e aggiungendo i termini necessari.
Un esempio
Faccio un esempio pratico per chiarire il processo.
Ho l'equazione generale della circonferenza:
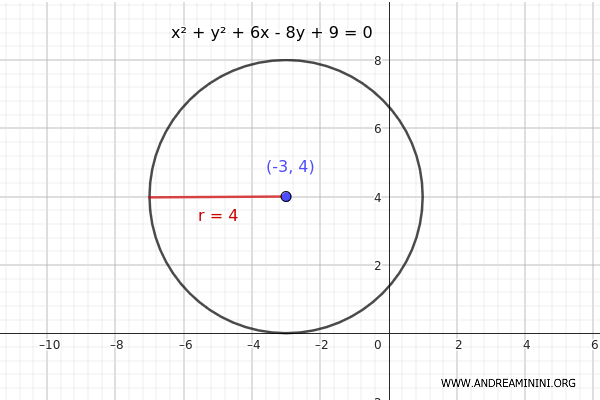
\[ x^2 + y^2 + 6x - 8y + 9 = 0 \]
Per trovare il centro della circonferenza, identifico i coefficienti \(D\) ed \(E\) nell'equazione. In questo caso sono:
$$ D = 6 $$
$$ E = -8 $$
Uso le formule per trovare le coordinate \(h\) e \(k\) del centro della circonferenza
$$ h = -\frac{D}{2} = -\frac{6}{2} = -3 $$
$$ k = -\frac{E}{2} = -\frac{-8}{2} = 4 $$
Quindi, il centro della circonferenza è \((-3, 4)\).
La dimostrazione
Per dimostrare come ottenere il centro della circonferenza dall'equazione generale \( x^2 + y^2 + Dx + Ey + F = 0 \), devo trasformare l'equazione nella forma standard \((x - h)^2 + (y - k)^2 = r^2\).
Considero l'equazione generale di una circonferenza
$$ x^2 + y^2 + Dx + Ey + F = 0 $$
Raggruppo i termini di \(x\) e \(y\):
$$ (x^2 + Dx) + (y^2 + Ey) + F = 0 $$
Completo il quadrato per i termini di \(x\) aggiungendo e sottraendo $ (\frac{D}{2})^2 $
$$ (x^2 + Dx + \left(\frac{D}{2}\right)^2 ) - \left(\frac{D}{2}\right)^2 + (y^2 + Ey) + F = 0 $$
$$ (x + \frac{D}{2})^2 - \left(\frac{D}{2}\right)^2 + (y^2 + Ey) + F = 0 $$
Completo il quadrato per i termini di \(y\) aggiungendo e sottraendo $ \left(\frac{E}{2}\right)^2 $
$$ \left(x + \frac{D}{2}\right)^2 - \left(\frac{D}{2}\right)^2 + (y^2 + Ey + \left(\frac{E}{2}\right)^2) \left(\frac{E}{2}\right)^2 + F = 0 $$
$$ \left(x + \frac{D}{2}\right)^2 - \left(\frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 - \left(\frac{E}{2}\right)^2 + F = 0 $$
Riorganizzo i termini:
$$ \left(x + \frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 = \left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2 - F $$
In questo modo ottengo l'equazione standard della circonferenza \((x - h)^2 + (y - k)^2 = r^2\), dove:
$$ h = -\frac{D}{2} $$
$$ k = -\frac{E}{2} $$
Quindi, il centro della circonferenza \((h, k)\) è:
$$ \left(-\frac{D}{2}, -\frac{E}{2}\right) $$
E il raggio \(r\) è:
$$ r = \sqrt{\left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2 - F} $$
Ho così dimostrato la formula per ottenere il centro e il raggio di una circonferenza quando l'equazione è in forma generale.
E così via.
