Poligoni regolari

I poligoni regolari sono figure geometriche piane che hanno tutti gli angoli e i lati congruenti.

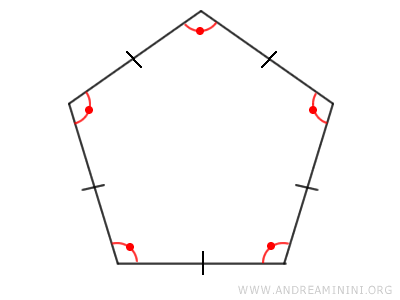
In altre parole, un poligono regolare è equilatero ed equiangolo, ossia ha tutti i suoi lati hanno la stessa lunghezza e tutti i suoi angoli hanno la stessa ampiezza.

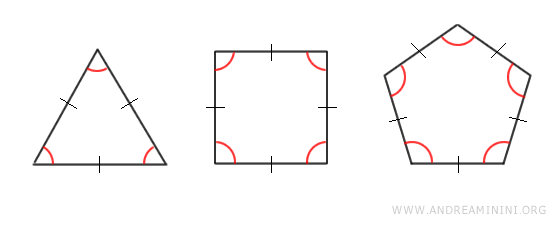
Esempi. Alcuni esempi notevoli di poligoni regolari includono il triangolo equilatero, il più semplice dei poligoni regolari con tre lati uguali e angoli di 60°, e il quadrato che ha quattro lati uguali e quattro angoli retti.

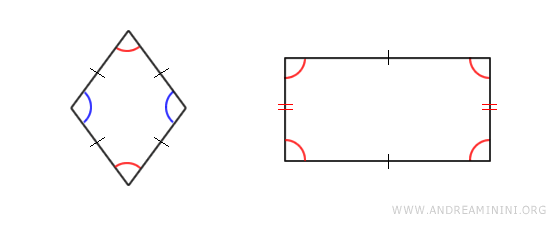
Viceversa, un rombo non è un poligono regolare perché, pur avendo tutti i lati congruenti, ha gli angoli non congruenti. Allo stesso modo, il rettangolo, non un poligono regolare perché, pur avendo tutti gli angoli retti, ha i lati di lunghezza diversa.

L'ampiezza degli angoli

In un poligono regolare con n lati, detto n-agono regolare, ogni angolo interno ha la stessa ampiezza (α) e può essere calcolato con la formula seguente:

$$ \alpha = (n−2) \cdot \frac{180°}{n} $$

Per esempio, in un esagono regolare (n=6 lati), ogni angolo interno misura 120°.

$$ \alpha = (6−2) \cdot \frac{180°}{6} = 4 \cdot 30° = 120° $$

Circonferenza inscritta e circoscritta dei poligoni regolari

Un poligono regolare è inscrivibile in una circonferenza esterna e circoscrivibile in un'altra circonferenza interna, entrambe le due circonferenze hanno lo stesso centro (O).

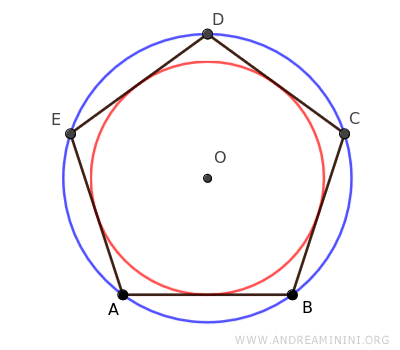
In altre parole, tutti i poligoni regolari possono essere inscritti in una circonferenza, cioè tutti i vertici toccano una circonferenza esterna.

Il raggio della circonferenza circoscritta (blu) è anche la distanza dal centro del poligono a ciascuno dei suoi vertici.

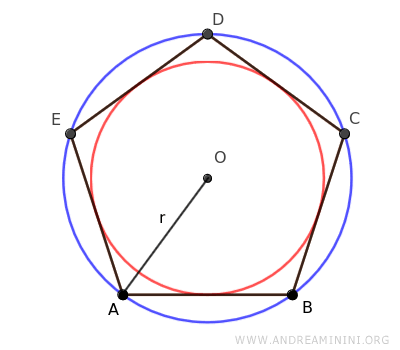
I poligoni regolari possono essere anche circoscritti a una circonferenza interna (rossa), dove tutti i lati sono tangenti alla circonferenza.

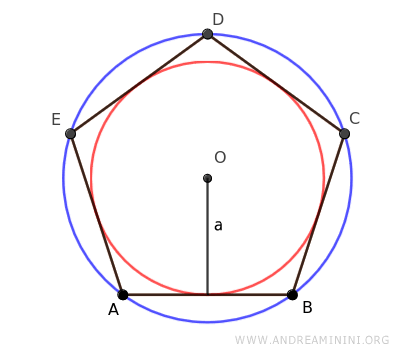
Il raggio della circonferenza inscritta è l'apotema (a),

La dimostrazione

Considero un poligono regolare come ipotesi iniziale. Ad esempio, un pentagono.

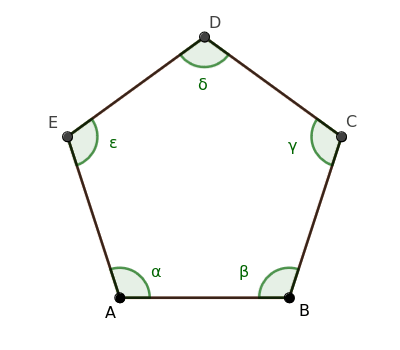
Essendo un poligono regolare è equilatero ed equiangolo.

$$ \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DE} \cong \overline{EA} $$

$$ \alpha \cong \beta \cong \gamma \cong \delta \cong \epsilon $$

Devo dimostrare che è inscrivibile in una circonferenza esterna e circoscrivibile a una circonferenza interna. Inoltre, devo dimostrare che le due circonferenze hanno lo stesso centro.

Traccio le bisettrici degli angoli α e β che dividono i due angoli in due metà congruenti α'≅α'' e β'≅β''.

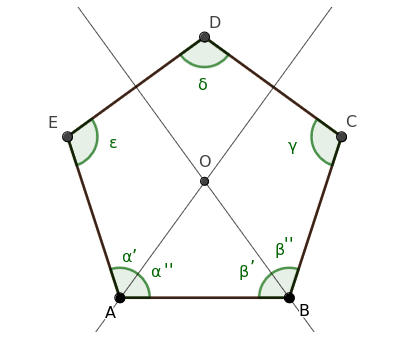
Indico con O il punto di intersezione delle due bisettrici.

Poiché α≅β sono angoli congruenti per l'ipotesi iniziale, sono congruenti anche le loro metà α'≅α''≅β'≅β''.

$$ \alpha' = \alpha'' \cong \beta' = \beta'' $$

Quindi, il triangolo ABO è un triangolo isoscele perché ha due angoli congruenti (α''≅β') alla base del triangolo.

 

Un triangolo isoscele ha due lati obliqui congruenti, quindi i due segmenti OA≅OB sono congruenti.

$$ \overline{OA} \cong \overline{OB} $$

Traccio il segmento OC tra il punto O e il vertice C del poligono regolare.

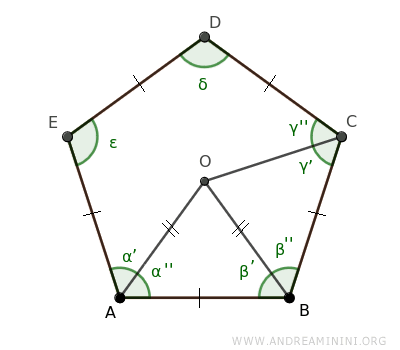
I triangolo ABO e BCO sono congruenti per il primo principio di congruenza dei triangoli, perché hanno un lato in comune (BO), un lato congruente (AB≅BC) e un angolo congruente per costruzione (β'≅β'').

Essendo due triangoli congruenti ABO≅BCO hanno tutti i lati e gli angoli congruenti nello stesso ordine.

Dunque i lati OC≅OB e gli angoli α''≅γ'. sono congruenti.

$$ \overline{OC} \cong \overline{OB} $$

$$ \alpha'' \cong \gamma' $$

Sapendo che α''≅γ' e α''≅α', per la proprietà transitiva deduco che α'≅α''≅γ'

$$ \alpha' \cong \alpha'' \cong \gamma' $$

Sapendo che α≅γ per l'ipotesi iniziale e α'+α''=α/2 per costruzione della bisettrice, deduco che anche γ'+γ''=γ/2

Quindi deduco che γ'≅γ'' e il segmento OC è la bisettrice dell'angolo γ.

$$ \gamma' \cong \gamma'' $$

Ripeto lo stesso procedimento per gli altri vertici del poligono regolare D, E scoprendo che anche i triangoli OCD≅ODE≅OEA sono triangoli isosceli congruenti.

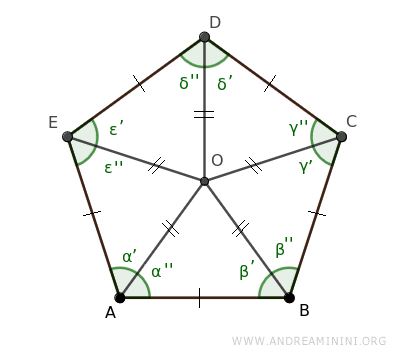
Pertanto, i segmenti OA, OB, OC, OD, OE sono congruenti

$$ \overline{OA} \cong \overline{OB} \cong \overline{OC} \cong \overline{OD} \cong \overline{OE} $$

Questo vuol dire che il punto O si trova alla stessa distanza dai vertici A, B, C, D, E del poligono regolare.

Essendo O equidistante dai vertici del poligono, posso tracciare una circonferenza che passa per tutti i vertici del poligono.

Ho così trovato la circonferenza in cui il poligono è inscritto.

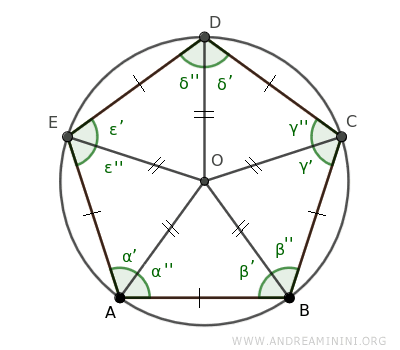
Il punto O è anche il punto di intersezione tra tutte le bisettrici dei triangoli isoscele OAB, OBC, OCD, ODE, OEA.

Sapendo che i punti di una bisettrice sono equidistanti dai lati dell'angolo, deduco che il punto O è equidistante da tutti i lati dei triangoli OAB, OBC, OCD, ODE, OEA.

Quindi, se traccio una circonferenza con centro O e raggio pari alla distanza tra D e un lato qualsiasi dei triangoli, la circonferenza tocca ed è tangente a tutti i lati del poligono regolare.

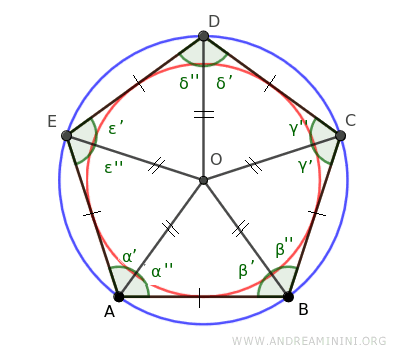
Ho così trovato la circonferenza interna, quella che il poligono circoscrive.

Inoltre, le due circonferenze, inscritta e circoscritta, hanno lo stesso centro O.

Questo dimostra il teorema iniziale.

L'apotema

L'apotema è la distanza più breve dal centro del poligono a uno qualsiasi dei suoi lati. E' il raggio della circonferenza inscritta.

Questo valore è particolarmente utile per calcolare l'area di un poligono regolare.

L'area (A) di un poligono regolare può essere trovata moltiplicando il perimetro (P) per l'apotema (a) e dividendo per due:

$$ A = \frac{P \cdot a}{2} $$

Esempio. Un pentagono ha tutti i lati lunghi 3 e un apotema a=2.06. Calcolo il perimetro del pentagono $$ P = 3 \cdot 5 = 15 $$ Poi, essendo noto l'apotema a=2.06, calcolo l'area del pentagono. $$ A = \frac{P \cdot a}{2} = \frac{15 \cdot 2.06}{2} = 15.45 $$ L'area del pentagono è A=15.45

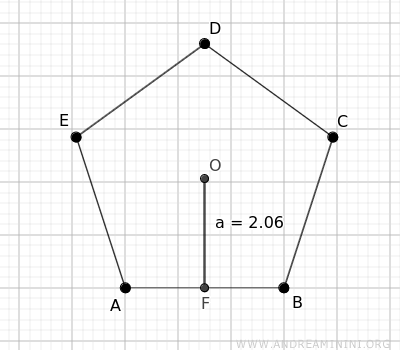
L'area del poligono regolare

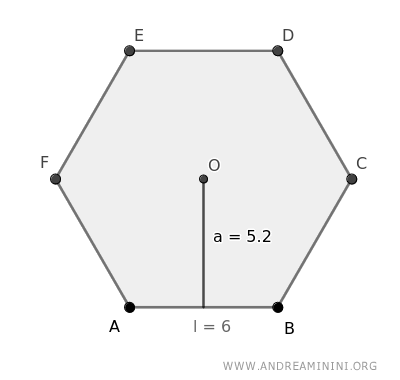
L'area del poligono regolare è uguale al prodotto tra il semiperimetro (p) e l'apotema (a) del poligono regolare. $$ A=p \cdot a $$

Dove l'apotema è il segmento che misura la distanza di ogni lato dal centro del poligono mentre il semiperimetro è la metà del perimetro 2p=P quindi p=P/2.

Questo accade perché il poligono regolare può essere suddiviso in più triangoli.

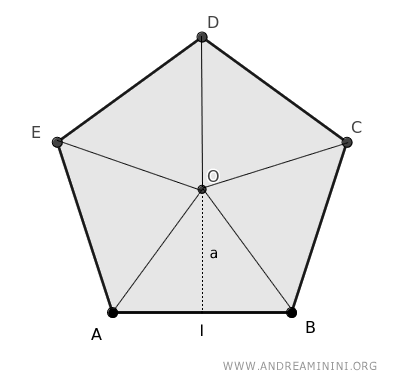
L'area di ogni triangolo si ottiene moltiplicando la base per l'altezza diviso due, ovvero il lato del poligono per l'apotema diviso due.

La somma delle aree dei triangoli è equivalente all'area complessiva del poligono regolare.

Il raggio di un poligono regolare

Il raggio di un poligono regolare è un segmento che collega il centro del poligono con uno qualsiasi dei suoi vertici.

E' il raggio della circonferenza circoscritta intorno al poligono, poiché tutti i vertici di un poligono regolare giacciono su una circonferenza il cui centro (O) è anche il centro del poligono.

Una proprietà interessante del raggio è che, in un poligono regolare, tutti i raggi sono congruenti, ovvero hanno tutti la stessa lunghezza.

Osservazioni

Alcune osservazioni e note a margine sui poligonI regolari

• Simmetria
  Ogni poligono regolare ha sia simmetria radiale che assiale. Il numero di assi di simmetria è uguale al numero di lati.
• Diagonali
  Il numero di diagonali D in un poligono regolare può essere calcolato tramite la formula $$ D=n(n−3)/2 $$ dove n è il numero di lati.

  Esempio. Un pentagono è composto da n=5 lati, quindi ha D=5 diagonali $$ D = 5 \cdot (5-3)/2 = 5 \cdot 2/2 = 5 $$ Per verificarlo basta tracciare tutte le diagonali possibili tra i vertici del pentagono. Sono 5 diagonali.
  

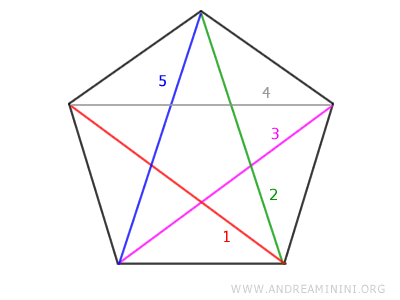
• Man mano che il numero dei lati aumenta, i poligoni regolari si avvicinano progressivamente alla forma di un cerchio pur restando dei poligoni con lati distinti, non importa quanti ne abbiano.
  
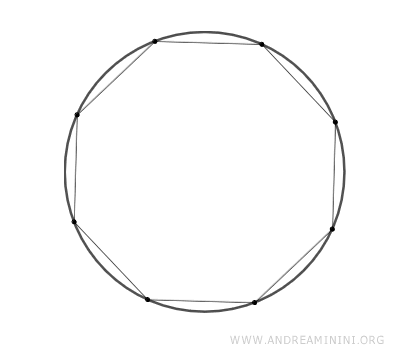
• Circonferenza inscritta e circoscritta
  Un poligono regolare è sempre circoscrivibile e inscrivibile in una circonferenza
  

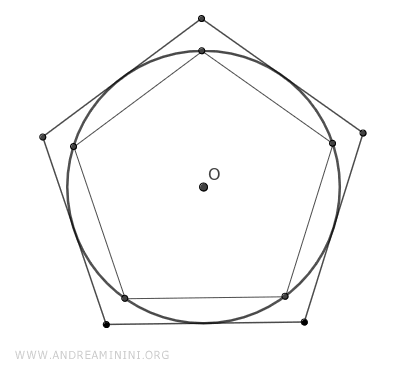
  Nota. Nel caso particolare dell'esagono regolare, il lato dell'esagono è sempre congruente con il raggio della circonferenza inscritta.

• Equivalenza tra poligono regolare e triangolo
  L'area del poligono regolare è uguale all'area di un triangolo che ha per base il perimetro del poligono regolare e per altezza l'apotema del poligono regolare.
  
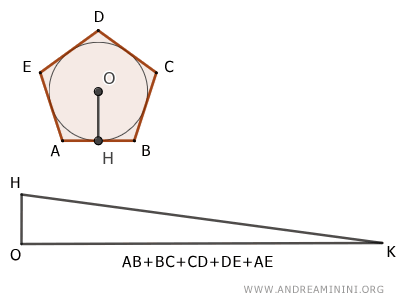
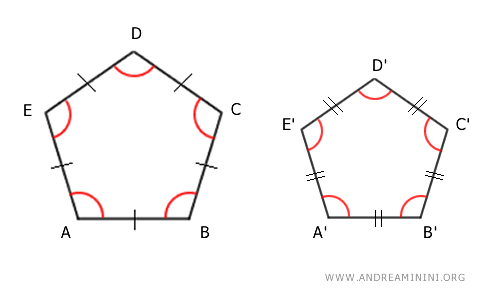
• Due poligoni regolari con lo stesso numero di lati sono poligoni simili
  Questo criterio semplifica la valutazione della similitudine tra due poligoni quando sono regolari e hanno lo stesso numero di lati.
  

E così via.