La circonferenza

La circonferenza è una figura geometrica piana composta dall'insieme dei punti del piano che hanno la stessa distanza costante (detta raggio "r") da un punto fisso O detto centro.

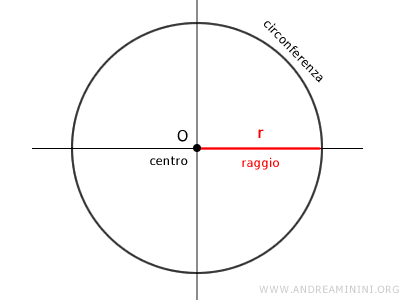
La circonferenza è il luogo geometrico dei punti che hanno la stessa distanza dal centro.

La distanza di ogni punto della circonferenza dal centro (O) è detta raggio.

In altre parole, la circonferenza è il perimetro o la linea di contorno di un cerchio. Dove il cerchio è la superficie della circonferenza.

Il cerchio può essere definito anche come il luogo geometrico dei punti che hanno una distanza dal centro della circonferenza minore o uguale al raggio. Qual è la differenza tra circonferenza e cerchio? La circonferenza è la linea che delimita una figura piana, mentre il cerchio è la figura piana delimitata da tale linea. In altre parole, la circonferenza è il perimetro o il bordo del cerchio, mentre il cerchio comprende anche il suo interno.

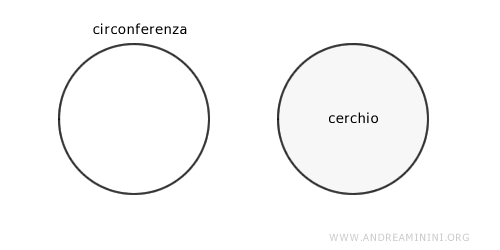
Pertanto, il cerchio è la figura piana che contiene i punti della circonferenza e i punti interni della circonferenza.

La lunghezza della circonferenza (C) è data dalla formula 2πr

$$ C = 2 \pi r $$

Dove r è il raggio e π (pi greco) è una costante matematica approssimativamente uguale a 3,14.

Sapendo che il diametro (d) è il doppio del raggio d=2r, si può scrivere anche in questa forma

$$ C = \pi \cdot d $$

Cos'è pi greco? Il rapporto tra la lunghezza di una circonferenza e il suo diametro è un valore costante, rappresentato dal simbolo π, noto come pi greco, e si avvicina al valore di 3,14. $$ π=3,14159 $$

Le formule della circonferenza

Le principali formule per calcolare le misure della circonferenza

• Lunghezza della circonferenza
  La lunghezza di una circonferenza (o perimetro) è data dalla formula 2πr, dove π è la costante matematica "pi greco" approssimativamente uguale a 3.14159 mentre "r" è il raggio. $$ C = 2 \cdot \pi \cdot r $$
• Area
  L'area del cerchio delimitato da una circonferenza è data dalla formula $$ A = \pi \cdot r^2 $$
• Raggio
  Il raggio è uguale alla circonferenza diviso per 2π $$ r = \frac{C}{2\pi} $$
• Diametro
  Il diametro è la distanza tra due punti opposti sulla circonferenza e passa attraverso il centro. È il doppio del raggio. $$ d = 2r $$

Il raggio

Il raggio di una circonferenza è un segmento che congiunge il centro O della circonferenza con un punto qualsiasi P della circonferenza.

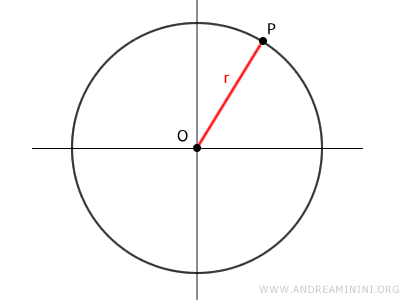
Pertanto, in una circonferenza esistono infiniti segmenti che identificano il raggio e sono congruenti tra loro perché hanno la stessa lunghezza.

La formula per calcolare il raggio è la seguente

$$ r = \frac{C}{2 \pi} $$

Sapendo che la circonferenza è uguale al doppio prodotto del raggio per pi greco $$ C = 2 \pi r $$ divido entrambi i membri dell'equazione per 2π e ottengo la formula del raggio $$ \frac{C}{2 \pi} = \frac{2 \pi r}{2 \pi} $$ $$ \frac{C}{2 \pi} = r $$

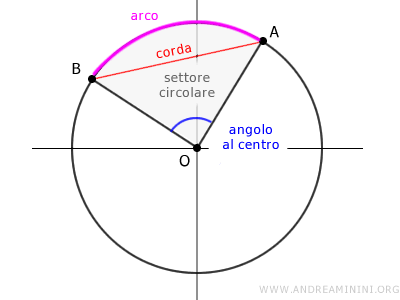
Gli archi

Due punti qualsiasi A e B su una circonferenza dividono la circonferenza in due parti detti archi.

Un arco è una parte della circonferenza delimitata tra un punto A a un punto B.

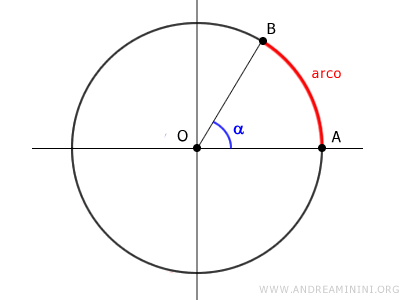
Per individuare la lunghezza dell'arco posso considerare l'ampiezza dell'angolo α

$$ l_a = 2 \pi r \cdot \frac{ \alpha }{360°} $$

Dove 2πr è la lunghezza della circonferenza.

Semplificando la formula della lunghezza dell'arco diventa:

$$ l_a = \pi r \cdot \frac{ \alpha }{180°} $$

Pertanto, c'è una stretta relazione tra la lunghezza dell'arco, l'ampiezza dell'angolo, il raggio della circonferenza.

Esempio. Se una circonferenza ha raggio r=5 e l'arco corrisponde a un angolo di α=45°, la lunghezza dell'arco è $$ l_a = 2 \pi r \cdot \frac{ \alpha }{360°} = 2 \cdot \pi \cdot 5 \cdot \frac{ 45° }{360°} = 3,92 $$

Le corde

Una corda di una circonferenza è un qualsiasi segmento che ha per estremi due punti A e B distinti sulla circonferenza.

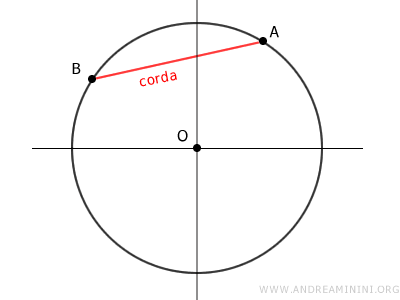
Se la corda passa anche per il centro è detta diametro della circonferenza.

Il diametro

Il diametro è un segmento che congiunge due punti distinti della circonferenza e passa per il centro della circonferenza.

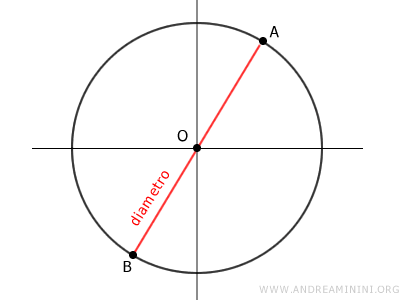
In pratica, il diametro è una particolare corda che attraversa il centro della circonferenza. E' la corda più lunga di una circonferenza.

La lunghezza del diametro è pari a 2r, due volte il raggio.

$$ d = 2r $$

Esistono infiniti segmenti che identificano il diametro di una circonferenza, tutti congruenti tra loro perché hanno la stessa lunghezza.

Il postulato della circonferenza

In un piano preso un punto O e un segmento AB qualsiasi, esiste una e una sola circonferenza che ha per centro il punto O e per raggio il segmento AB

L'equazione della circonferenza

L'equazione in forma standard della circonferenza sul piano cartesiano è la seguente:

$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$

Dove (x₀; y₀) sono le coordinate del centro O della circonferenza e r è il raggio della circonferenza.

In alternativa, posso scrivere l'equazione generale della circonferenza

$$ x^2+ y^2+ ax +by+ c = 0 $$

Dove i parametri sono a=-2x₀, b=-2y₀, c=x₀²+y₀²-r²

In questo caso le coordinate (x_0; y₀) del centro della circonferenza sono:

$$ (x_0 ; y_0) = ( - \frac{a}{2} ; - \frac{b}{2} ) $$

Mentre il raggio si ottiene in questo modo

$$ r = \sqrt{ ( - \frac{a}{2} )^2 + ( - \frac{b}{2} )^2 - c } $$

L'equazione della circonferenza può essere scritta anche in questa forma equivalente esplicita $$ y = y_0 \pm \sqrt{r^2 - (x-x_0)^2 } $$

Esempio

Voglio tracciare una circonferenza che ha per centro il punto (x;y)=(1;3) e raggio r=2.

In questo caso x₀=1 e y₀=3

$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$

$$ (x - 1)^2 + (y - 3)^2 = r^2 $$

Il raggio della circonferenza è r=2

$$ (x - 1)^2 + (y - 3)^2 = 2^2 $$

$$ (x - 1)^2 + (y - 3)^2 = 4 $$

Questa equazione è soddisfatta da tutti i punti che distano 4 dal punto (1;3) del piano.

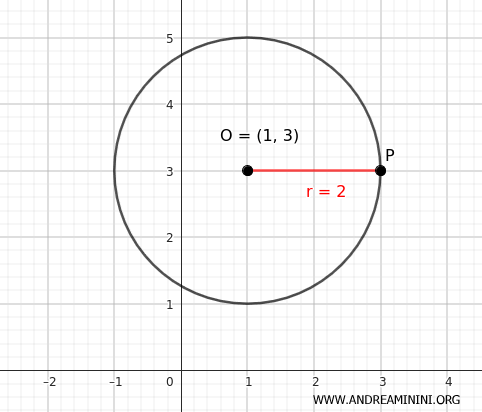
In questo modo ho delineato la circonferenza che volevo costruire.

La dimostrazione

Considero una circonferenza di raggio "r" e centro O(x₀;y₀).

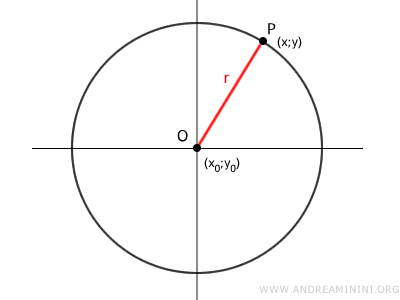
Un generico punto P(x;y) del piano appartiene alla circonferenza se e solo se dista dal centro O una lunghezza pari al raggio r della circonferenza.

$$ \overline{OP} = r $$

Elevo al quadrato entrambi i membri dell'equazione

$$ \overline{OP}^2 = r^2 $$

La lunghezza del segmento OP è uguale alla distanza tra i punti O e P che si misura usando il teorema di Pitagora.

$$ \overline{OP} = \sqrt{ (x-x_0)^2 + (y-y_0)^2 } $$

Quindi, posso riscrivere l'equazione in questa forma equivalente

$$ \overline{OP}^2 = r^2 $$

$$ ( \sqrt{ (x-x_0)^2 + (y-y_0)^2 } )^2 = r^2 $$

Il risultato finale è l'equazione in forma standard della circonferenza.

$$ (x-x_0)^2 + (y-y_0)^2 = r^2 $$ 

A questo punto, per ottenere anche l'altra formula svolgo i due quadrati

$$ x^2+x_0^2-2xx_0 + y^2+y_0^2-2yy_0 = r^2 $$

$$ x^2+ y^2-2xx_0 -2yy_0+x_0^2 +y_0^2 - r^2 = 0 $$

Considero a=-2x₀, b=-2y₀, c=x₀²+y₀²-r²

$$ x^2+ y^2-2x_0 \cdot x - 2y_0 \cdot y+( x_0^2 + y_0^2 - r^2 ) = 0 $$

$$ x^2+ y^2+ a \cdot x +b \cdot y+ c = 0 $$

Il risultato finale è l'equazione generale della circonferenza.

$$ x^2+ y^2+ ax +by+ c = 0 $$

Sapendo che a=-2x₀ e b=-2y₀ , ricavo le coordinate x₀=-a/2 e y₀=-b/2

Quindi, le coordinate (x_0; y₀) del centro della circonferenza sono

$$ (x_0 ; y_0) = ( - \frac{a}{2} ; - \frac{b}{2} ) $$

Per ottenere la formula del raggio confronto le due equazioni della circonferenza \( x^2+x_0^2+ \frac{a}{2} x + \frac{b}{2}y + y^2+y_0^2 - r^2 = 0 \) con quelli dell'equazione \( x^2+ y^2+ ax +by+ c = 0 \)

• Equazione standard della circonferenza
  $$ x^2+x_0^2+ \frac{a}{2} x + \frac{b}{2}y + y^2+y_0^2 - r^2 = 0 $$
• Equazione generale della circonferenza
  $$ x^2+ y^2+ ax +by+ c = 0 $$

I termini costanti nelle due equazioni sono r², x₀² e y₀² nella prima equazione e c nella seconda equazione

Nota. Dove per "termine costante" intendo quei termini che non sono moltiplicati per una variabile, quindi sono costanti perché il loro valore non cambia a prescindere dai valori delle variabili x e y dell'equazione.

Essendo costanti, questi termini devono essere uguali in entrambe le equazioni.

In altre parole, la somma dei termini costanti della prima equazione x₀²+y₀²-r² è uguale al termine "c" della seconda equazione della circonferenza.

Quindi, comparo ed eguaglio i termini costanti delle due equazioni.

$$ x_0^2 + y_0^2 - r^2 = c $$

In questo modo posso ricavare il raggio r della circonferenza

$$ r^2 = x_0^2 + y_0^2 - c $$

$$ \sqrt{ r^2 } = \sqrt{ x_0^2 + y_0^2 - c } $$

$$ r = \sqrt{ x_0^2 + y_0^2 - c } $$

Sapendo che a=-2x₀, b=-2y₀, ricavo le coordinate x₀=-a/2 e y₀=-b/2

$$ r = \sqrt{ ( - \frac{a}{2} )^2 + ( - \frac{b}{2} )^2 - c } $$

E' la formula del raggio che volevo ottenere

Osservazioni

Alcune osservazioni sulle circonferenze

• Una circonferenza è una figura simmetrica rispetto al proprio centro e rispetto a qualsiasi retta passante per il cerchio.
• La circonferenza è convessa, perché presi due punti qualsiasi della circonferenza, il segmento che li unisce è interamente contenuto dentro di essa.
• I principi di congruenza in una circonferenza
  Se in una circonferenza sono congruenti: due corde, due archi, due settori circolari, due segmenti circolari o due angoli al centro, allora sono congruenti anche tutti gli altri. Questo accade perché queste grandezze sono tra loro corrispondenti in modo biunivoco. Ad esempio, a un angolo al centro corrisponde un arco e viceversa.
  

E così via