Settore circolare
Il settore circolare è una parte di un cerchio delimitata da due raggi e dall'arco di cerchio compreso tra questi.
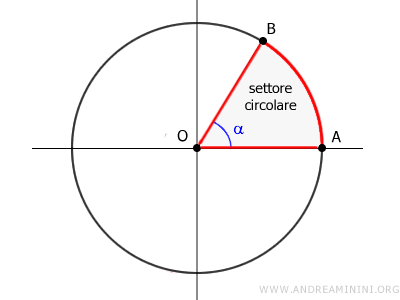
L'ampiezza dell'angolo al centro, formato dai due raggi, determina la grandezza del settore.
L'arco è una porzione di circonferenza del cerchio compresa tra i due raggi.
Dove l'angolo al centro è l'angolo formato dai due raggi del settore, mentre il raggio è un segmento che ha per estremi il centro del cerchio e un punto della circonferenza.
La parte di cerchio tra un arco e la corda che lo sottende è detta segmento circolare a una base.
Le proprietà e le formule
La lunghezza (L) dell'arco di un settore può essere calcolata utilizzando la formula:
$$ L = \frac{\alpha}{360} \cdot 2\pi r = \frac{\alpha}{180} \cdot \pi r $$
Dove α è l'ampiezza dell'angolo al centro misurata in gradi e r è il raggio del cerchio.
L'area (As) di un settore può essere calcolata utilizzando la formula:
$$ A_s = \frac{\alpha}{360} \cdot \pi r^2 $$
Se l'angolo α è misurato in radianti, la formula per calcolare l'area del settore è la seguente:
$$ A_s = \frac{\alpha_{rad}}{2} \cdot r^2 $$
Dimostrazione. L'area del settore circolare è direttamente proporzionale all'ampiezza dell'angolo al centro $$ A_s : A = \alpha:360 $$ L'area del settore circolare As sta all'area del cerchio A come l'angolo al centro α sta all'angolo giro (360°). Rappresento la proporzione in una frazione. $$ \frac{A_s}{A} = \frac{\alpha}{360} $$ Divido entrambi i membri dell'equazione per A. $$ A_s = \frac{\alpha}{360} \cdot A $$ Sapendo che l'area del cerchio è A=πr2 ottengo la formula che volevo dimostrare. $$ A_s = \frac{\alpha}{360} \cdot \pi r^2 $$ Per ottenere la formula in radianti basta considerare che l'angolo giro (360°) equivale a 2π radianti e semplificare. $$ A_s = \frac{\alpha_{rad}}{2 \pi} \cdot \pi r^2 = \frac{\alpha_{rad}}{2} \cdot r^2 $$
In alternativa, la superficie del settore circolare può essere calcolata anche a partire dalla lunghezza dell'arco, con l'angolo misurato in gradi.
$$ A_s = \frac{1}{2} \cdot L \cdot r $$
Dimostrazione. Considero la formula per calcolare l'area del settore circolare a partire da un angolo misurato in gradi. $$ A_s = \frac{\alpha}{360} \cdot \pi r^2 $$ Divido entrambi i membri dell'equazione per la lunghezza dell'arco L. $$ \frac{ A_s }{L} = \frac{ \frac{\alpha}{360} \cdot \pi r^2 }{L} $$ Sapendo che la lunghezza dell'arco è $ L = \frac{\alpha}{360} \cdot 2\pi r $ $$ \frac{ A_s }{L} = \frac{ \frac{\alpha}{360} \cdot \pi r^2 }{ \frac{\alpha}{360} \cdot 2\pi r } $$ Poi semplifico $$ \frac{ A_s }{L} = \frac{ r }{ 2 } $$ In questo modo ottengo la formula $$ A_s = \frac{ 1}{ 2 } \cdot L \cdot r $$
E così via.
