Corde di una circonferenza
Una corda è un segmento di retta che unisce due punti distinti sulla circonferenza.
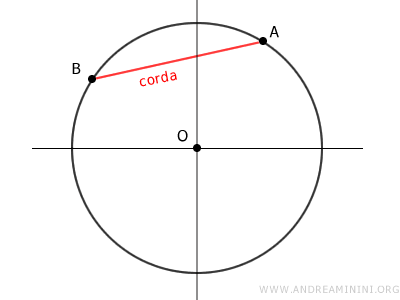
Il diametro è un caso speciale di corda, essendo la corda più lunga possibile in una circonferenza.
A differenza del diametro, tutte le altre corde non passano per il centro della circonferenza.
Secondo un'accezione più generale, la corda è un segmento con gli estremi su due punti diversi di una curva, di un'ellisse o di un'iperbole oppure su due lati distinti di una poligonale. Va però ricordato che, in questi casi, le proprietà delle corde possono variare a seconda della curva in questione.
Gli estremi di una corda dividono la circonferenza in due archi.
In questi casi si dice che la corda sottende i due archi oppure che ogni arco è sotteso dalla corda.
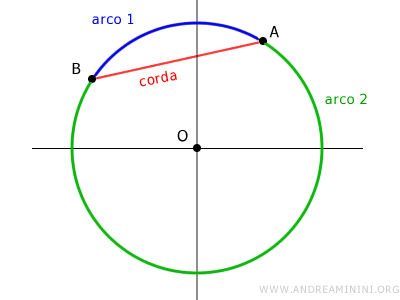
Quindi, per indicare a quale arco di una corda voglio riferirmi, è necessario aggiungere un terzo punto situato sull'arco oppure fissare una convenzione (es. senso antiorario tra gli estremi).
La retta a cui appartiene una corda è detta retta secante.
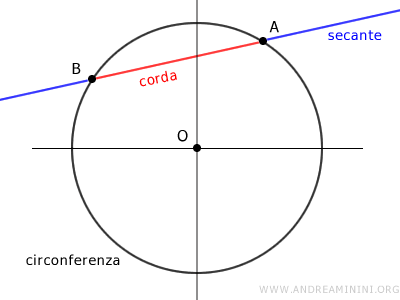
La corda e l'arco di curva corrispondente determinano una regione di piano finita detta segmento di circonferenza, o segmento di curva se si tratta di una curva.
Osservazioni
Alcune note e proprietà sulle corde di una circonferenza
- L'asse di una corda qualsiasi passa per il centro della circonferenza
Presa una corda qualsiasi con estremi A e B sulla circonferenza, il segmento AB ha l'asse che passa per il centro della circonferenza. Dove per "asse" intendo la retta perpendicolare al segmento che passa per il suo punto medio.
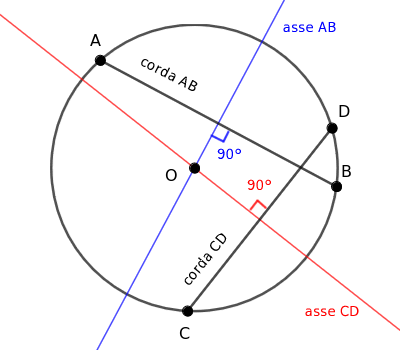
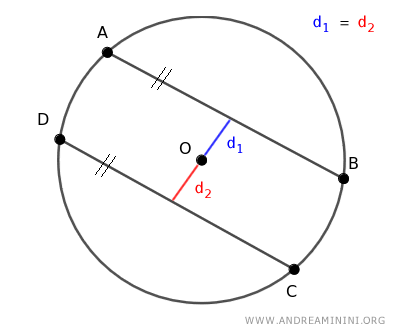
- Due corde sono congruenti se e solo se sono equidistanti dal centro della circonferenza
Per essere congruenti due corde AB≅CD devono avere la stessa distanza dal centro O della circonferenza d1=d2.
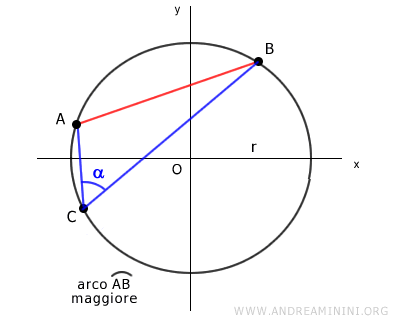
- Teorema delle corde
La lunghezza di una corda AB di una circonferenza di raggio r è uguale al doppio prodotto del raggio 2r per il seno di uno degli angoli alla circonferenza α che insistono sulla corda. $$ AB = 2r \sin \alpha $$
E così via
