La retta polare delle tangenti

La retta polare delle tangenti è una retta r associata a un punto P esterno a una conica (ad esempio, una circonferenza), tale che i punti di contatto A e B tra r e la conica sono anche i punti di contatto delle tangenti alla conica che passano per P.

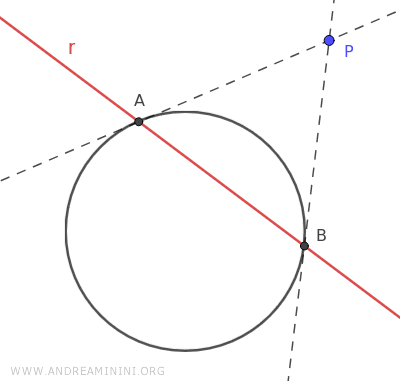
Per comprendere meglio, considero una circonferenza \(\mathcal{C}\) e un punto \(P\) esterno a essa.

Traccio le tangenti della circonferenza che passano per il punto esterno P.

Poiché P è un punto esterno alla circonferenza, ci sono due rette tangenti e altrettanti punti di contatto con la circonferenza.

La retta polare associata a P è la retta (rossa) che passa tra i due punti di tangenza A e B sulla circonferenza.

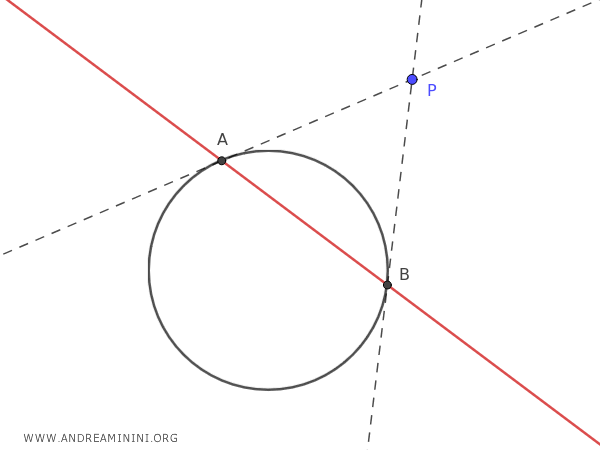
Per trovare l'equazione della retta polare in una conica $ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $ e un punto $ P(x_0, y_0) $ posso usare le formule di sdoppiamento

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Nota. La retta polare delle tangenti rappresenta un collegamento tra una conica e un punto esterno qualsiasi, tramite il luogo geometrico delle tangenti alla conica che passano per quel punto.

Esempio Pratico

Prendo come esempio di conica una circonferenza e un punto \( Q(6, 8) \) esterno alla circonferenza.

$$ x^2 + y^2 - 25 = 0 $$

$$ Q(6,8) $$

Utilizzo la formula di sdoppiamento

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Sostituisco i coefficienti della conica A=1, B=0, C=1, D=0, E=0, F=-25

$$ 1 \cdot xx_0 + 0 \cdot \left(\frac{xy_0 + yx_0}{2}\right) + 1 \cdot yy_0 + 0 \cdot x + 0 \cdot y - 25 = 0 $$

$$ xx_0 +  yy_0 - 25 = 0 $$

Spiegazione. Una conica è rappresentata in generale dall'equazione  $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$ In questo caso si tratta di una circonferenza $$ x^2 + y^2 = 25 $$ Quindi, i coefficienti sono A=1, B=0, C=1, D=0, E=0, F=-25

Le coordinate del punto esterno Q(6,8) sono x₀=6 e y₀=8.

$$ x \cdot 6 +  y \cdot 8 - 25 = 0 $$

Ho così trovato l'equazione della retta polare.

$$ 6x +  8y - 25 = 0 $$

Questa retta rappresenta la retta polare del punto \( Q(6, 8) \) rispetto alla circonferenza \( x^2 + y^2 = 25 \).

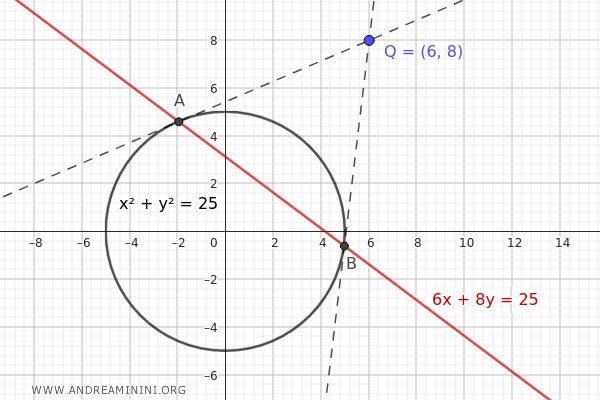
Come si può vedere nel grafico, i due punti di intersezione A e B della retta polare sulla circonferenza coincidono con i punti di contatto delle due rette tangenti che passano per il punto esterno \( Q(6, 8) \).

Osservazioni

Alcune osservazioni utili sulla retta polare

• Se il punto P è un punto della circonferenza la polare coincide con la tangente di P
  Quando un punto P si trova su una conica, come una circonferenza, la sua retta polare coincide con la tangente alla conica in quel punto.

  Esempio. Considero una circonferenza con centro nell'origine e raggio r=25. $$ x^2 + y^2 = 25 $$ Poi prendo il punto \(P(3, 4)\) che si trova esattamente sulla circonferenza. Applico la formula di sdoppiamento $$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$ In questo caso i coefficienti sono A=1, B=0, C=1, D=0, E=0, F=-25 $$ xx_0  + yy_0 - 25 = 0 $$ Le coordinate del punto P(3,4) sono x₀=3 e y₀=4. $$ 3x + 4y - 25 = 0 $$ Questa equazione rappresenta una retta tangente alla circonferenza che passa per il punto P(3,4).
  

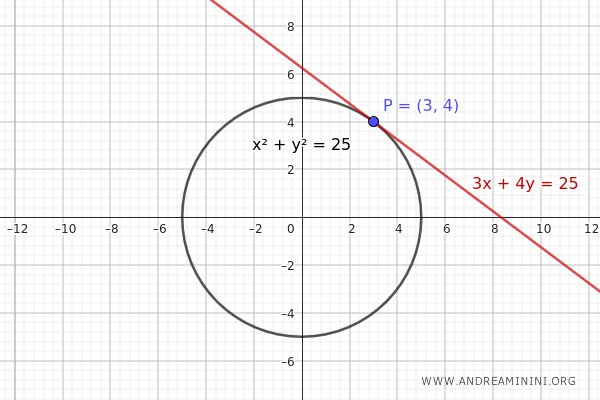
• Se il punto P è interno alla circonferenza, non esiste una tangente reale, né una secante
  Se il punto P è interno alla circonferenza, allora l'equazione della retta associata al punto è esterna alla circonferenza. Quindi, non esiste alcuna tangente reale, né una secante alla circonferenza. Tuttavia, il concetto di retta polare si estende anche a questo caso, e la polare di un punto interno è ancora ben definita geometricamente, anche se non rappresenta più una tangente reale.
  

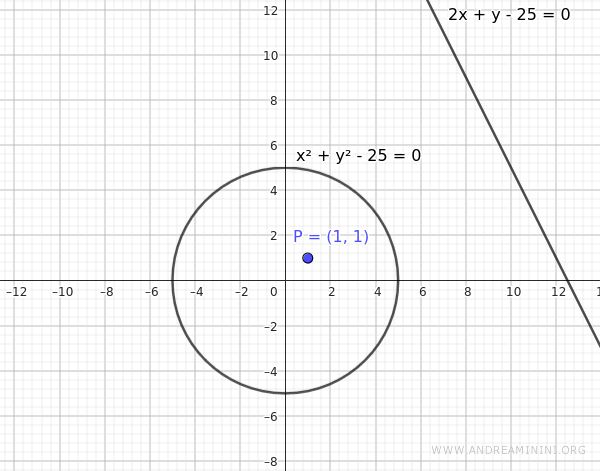
  Esempio. Considero la stessa circonferenza dell'esempio precedente $$ x^2 + y^2 = 25 $$ ma questa volta prendo in considerazione il punto interno $ P(2,1) $. Applico di nuovo la formula di sdoppiamento $$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$ In questo esempio i coefficienti sono A=1, B=0, C=1, D=0, E=0, F=-25 $$ xx_0  + yy_0 - 25 = 0 $$ Le coordinate del punto P(2,1) sono x₀=2 e y₀=1. $$ 2x + y - 25 = 0 $$ Questa equazione rappresenta una retta esterna alla circonferenza, quindi non è una tangente reale, né interseca la circonferenza in alcun punto.
  

E così via