Teorema delle tangenti a una circonferenza da un punto esterno

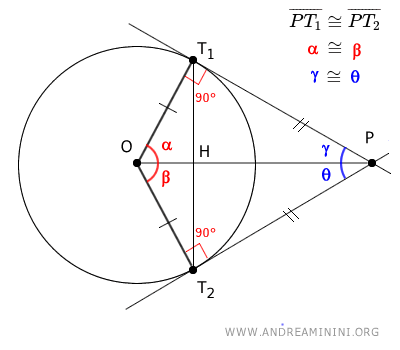
Considerando una circonferenza e due rette tangenti ad essa che passano per un punto P esterno alla circonferenza, i segmenti formati tra il punto P e i rispettivi punti di tangenza, T₁ e T₂, sulla circonferenza sono congruenti $ \overline{PT_1} \cong \overline{PT_2} $ (ossia, di uguale lunghezza) .

 

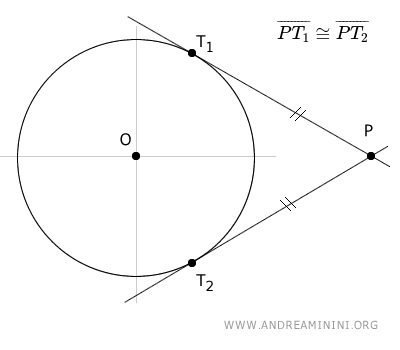
Inoltre, si presentano tre interessanti proprietà che è utile ricordare:

• Il segmento OP, che congiunge il centro O della circonferenza con il punto esterno P, è l'asse della corda tra i punti di tangenza T₁ e T₂ e funge da asse simmetrico per i segmenti PT₁ e PT₂.
  
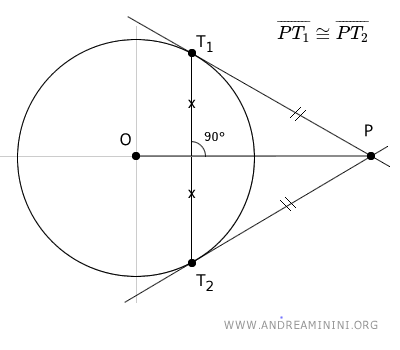
• Il segmento OP è bisettrice dell'angolo (rosso) formato dai raggi della circonferenza che congiungono il centro O con i punti di tangenza T₁ e T₂.
  
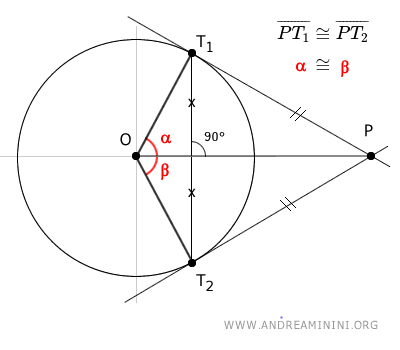
• Il segmento OP funge anche da bisettrice dell'angolo (blu) formato dalle due rette tangenti PT₁ e PT₂ in corrispondenza del punto P.
  

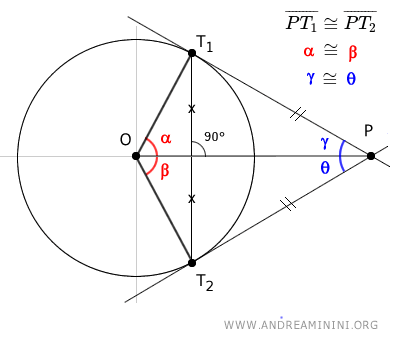
La dimostrazione

Considero una circonferenza di raggio OT₁ e due rette tangenti alla circonferenza PT₁ e PT₂ che passano per il punto esterno P.

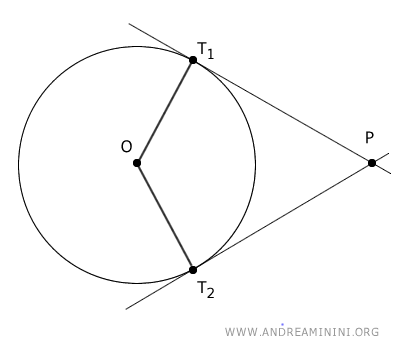
Traccio il segmento che congiunge il centro della circonferenza O con il punto esterno P.

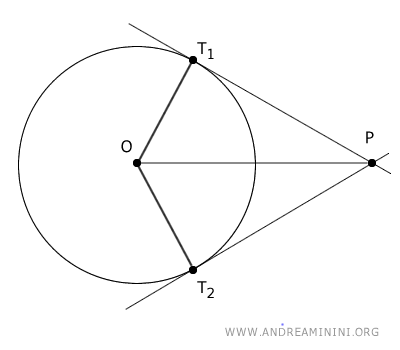
I punti di tangenza sulla circonferenza sono T₁ e T₂

I due segmenti OT₁ e OT₂ sono congruenti perché sono entrambi due raggi della circonferenza.

$$ \overline{OT_2} \perp \overline{OT_2} $$

Sapendo che i raggi della circonferenza sono sempre perpendicolari alle rette tangenti, deduco che i raggi OT₁ e OT₂ formano un angolo di 90° rispettivamente con i segmenti PT₁ e PT₂.

$$ \overline{OT_1} \perp \overline{PT_1} $$

$$ \overline{OT_2} \perp \overline{PT_2} $$

Pertanto, i triangoli OPT1 e OPT2 sono due triangoli rettangoli.

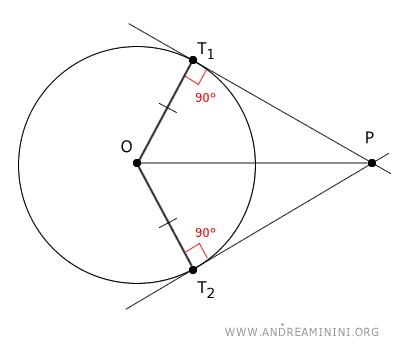
I due triangoli rettangoli OPT₁ e OPT₂ sono congruenti per il teorema di congruenza dei triangoli rettangoli, perché hanno un cateto congruente OT₁=OT₂ e l'ipotenusa coincidente OP.

$$ OPT_1 \cong OPT_2 $$

Essendo due triangoli congruenti, hanno tutti i lati e gli angoli congruenti nello stesso ordine.

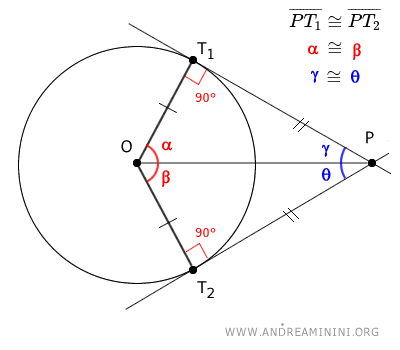
Questo dimostra che i segmenti PT₁ e PT₂ sono congruenti

$$ \overline{PT_1} \cong \overline{PT_2} $$

Inoltre, gli angoli α=β e γ=θ sono congruenti.

$$ \alpha \cong \beta $$ $$ \gamma \cong θ $$

Di conseguenza, il segmento OP è la bisettrice dell'angolo al centro O formato dai raggi e dell'angolo tra le rette tangenti nel vertice P.

Infine, traccio la corda T₁T₂ tra i due punti di tangenza.

Il triangolo OT₁T₂ è un triangolo isoscele perché i due lati obliqui sono congruenti OT₁≅OT₂, in quanto sono due raggi della circonferenza.

Il segmento OH è una bisettrice del triangolo perché so già che gli angoli α≅β sono congruenti.

Sapendo che in un triangolo isoscele la bisettrice coincide, con l'altezza, l'asse e con la mediana, deduco che:

• il segmento OH è perpendicolare alla corda T₁T₂ in quanto OH è un'altezza del triangolo
• il punto H è il punto medio della corda T₁T₂ in quanto OH è anche la mediana

Quindi il segmento OH è un asse del triangolo OT₁T₂.

Poiché OH appartiene al segmento OP, questo dimostra che il segmento OP è l'asse della corda T₁T₂ tra i due punti di tangenza.

E così via.