Principi di congruenza nella circonferenza
All'interno di una circonferenza, se si verifica una congruenza tra:
- due angoli al centro
- due archi
- due corde
- due segmenti circolari
- due settori circolari
allora tutte le figure corrispondenti sono congruenti.
In altre parole, in una circonferenza queste figure geometriche sono interconnesse e la congruenza di una di queste (angoli al centro, corde, ecc.) implica la congruenza anche delle altre.
Nota. Tuttavia, occorre sottolineare che la congruenza tra gli elementi all'interno di una singola circonferenza, come angoli al centro, archi, corde, settori circolari e segmenti circolari, non implica necessariamente che due circonferenze diverse siano congruenti tra loro. Per determinare se due circonferenze sono congruenti, l'unico criterio è confrontare i loro raggi.
Questo fenomeno si verifica perché ogni figura menzionata determina le altre. In altre parole, l'arco, l'angolo al centro, le corde, il settore circolare e il segmento circolare sono intrinsecamente collegati.
Ad esempio, considero una corda AB in una circonferenza.
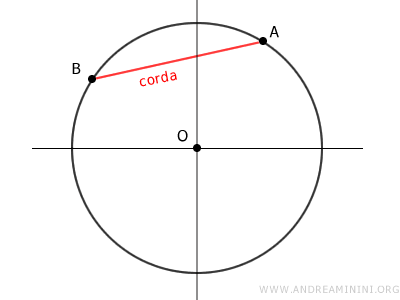
La corda AB determina un arco AB sulla circonferenza, che a sua volta corrisponde a un angolo al centro α, un settore circolare e un segmento circolare.
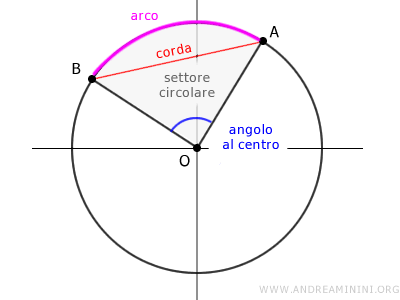
Queste corrispondenze sono biunivoche, il che significa che a un arco corrisponde precisamente un angolo al centro e viceversa.
Quindi, la congruenza tra due corde di una circonferenza implica la congruenza anche dei rispettivi archi, settori circolari, corde e angoli al centro.
E così via per le altre figure.
