Circonferenze interne e concentriche

Una circonferenza è interna a un'altra circonferenza, detta esterna, se la distanza tra i centri OO' è inferiore alla differenza dei raggi $$ \overline{OO'} < r-r' $$

Dove OO′ rappresenta la distanza tra i centri delle due circonferenze e r e r' sono rispettivamente i raggi della circonferenza esterna e interna.

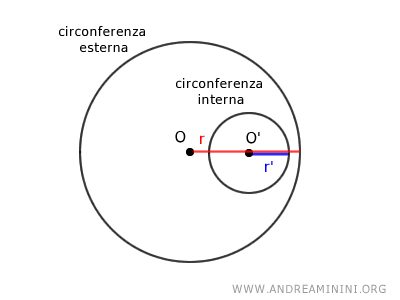
In questo caso il presupposto è che tutti i punti di una circonferenza si trovino all'interno di un'altra circonferenza.

Questo è possibile solo se si verificano due condizioni

• Il centro della circonferenza interna O' è un punto interno dell'altra circonferenza esterna.
• Il raggio della circonferenza interna r' sommato alla distanza tra i due centri OO' è inferiore al raggio della circonferenza esterna $$ \overline{OO'} + r' < r $$

Queste condizioni garantiscono che tutti i punti della circonferenza siano punti interni della circonferenza più esterna.

Nota. Nel caso particolare in cui le due circonferenze hanno lo stesso centro O=O' ma raggio diverso r≠r', sono dette circonferenze concentriche. In questo caso la distanza tra i due centri è ovviamente nulla OO'=0.

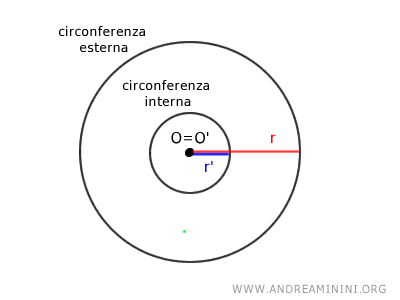
Le circonferenze sono invece circonferenze coincidenti se hanno lo stesso centro O=O' e lo stesso raggio r=r'.

Un esempio pratico

Considero due circonferenze.

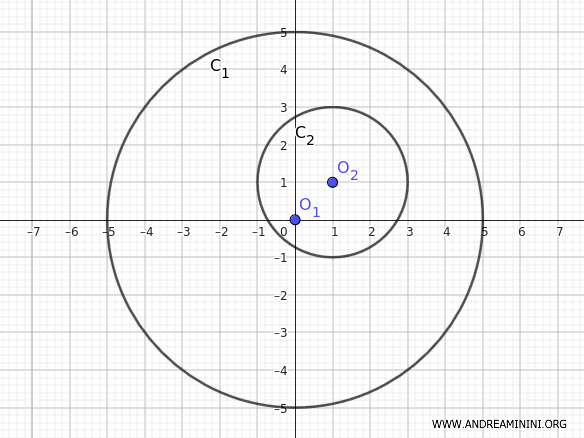
1. La prima circonferenza \( C_1 \) ha centro \( O_1 = (0, 0) \) e raggio \( r_1 = 5 \) cm.
2. La seconda circonferenza \( C_2 \) ha centro \( O_2 = (1, 1) \) e raggio \( r_2 = 2 \) cm.

Calcolo la distanza tra i centri \( O_1 \) e \( O_2 \) delle due circonferenze usando la formula della distanza euclidea.

$$ d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} $$

In questo caso \( O1 = (0,0) \) e \( O2 = (1,1) \) , quindi \( x_1 = 0 , y_1 = 0 , x_2=1, y_2 = 1 \)

$$ d = \sqrt{(1-0)^2 + (1-0)^2} $$

$$ d = \sqrt{1 + 1} $$

$$ d = \sqrt{2} \approx 1.41 \text{ cm} $$

A questo punto verifico se una circonferenza è dentro l'altra.

Una circonferenza è interna se la distanza tra i centri è minore della differenza dei raggi in valore assoluto:

$$ d < | r_1 - r_2 | $$

La distanza tra i centri è circa $ d=1.41 cm $ mentre i raggi sono $ r_1 = 5 $ cm e $ r_2 = 2 $ cm.

$$ 1.41 < 5 - 2 $$

$$ 1.41 < 3 $$

Quindi, la circonferenza con il raggio più piccolo \( C_2 \) è interna alla circonferenza \( C_1 \).

Le circonferenze interne in geometria analitica

Per determinare se una circonferenza è interna a un'altra utilizzando le equazioni delle circonferenze, devo individuare e confrontare i raggi e le posizioni dei loro centri.

Supponiamo di avere due circonferenze con le seguenti equazioni:

$$ C_1: x^2 + y^2 + a_1x + b_1y + c_1 = 0 $$

$$ C_2: x^2 + y^2 + a_2x + b_2y + c_2 = 0 $$

Per prima cosa trovo i centri e i raggi delle due circonferenze.

Nota. Per trovare i potrei applicare direttamente la formula delle coordinate del centro di una circonferenza $$ \left(-\frac{a}{2}, -\frac{b}{2}\right) $$ e la formula del raggio $$ r = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2 - c} $$ Tuttavia, preferisco fare tutti i passaggi perché la procedura generale mi permette di risolvere il problema anche nei casi in cui non dovessi ricordare le formule del centro e del raggio.

Per trovare i centri delle circonferenze, mi conviene riscrivere le equazioni delle circonferenze nella forma standard:

$$  (x-h)^2 + (y-k)^2 = r^2 $$

Dove \((h, k)\) è il centro e \(r\) è il raggio.

1] La prima circonferenza in forma standard

Per la prima circonferenza \( x^2 + y^2 + a_1x + b_1y + c_1 = 0 \):

\[ x^2 + a_1x + y^2 + b_1y = -c_1 \]

Completo il quadrato per i termini \( x \) e \( y \):

\[ x^2 + a_1x + \left(\frac{a_1}{2}\right)^2 + y^2 + b_1y + \left(\frac{b_1}{2}\right)^2 = -c_1 + \left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 \]

In questo modo ottengo l'equazione in forma standard.

\[ \left(x + \frac{a_1}{2}\right)^2 + \left(y + \frac{b_1}{2}\right)^2 = \left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 - c_1 \]

In questa forma è molto facile individuare le coordinate del centro e il raggio.

• Il centro della prima circonferenza è $$ \left(-\frac{a_1}{2}, -\frac{b_1}{2}\right) $$
• Il raggio della prima circonferenza è $$ r_1 = \sqrt{\left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 - c_1} $$

2] La seconda circonferenza in forma standard

Analogamente, svolgo gli stessi calcoli anche per la seconda circonferenza.

$$  x^2 + y^2 + a_2x + b_2y + c_2 = 0  $$

$$  x^2 + y^2 + a_2x + b_2y  = - c_2  $$

Completo il quadrato per i termini \( x \) e \( y \):

\[ x^2 + a_2x + \left(\frac{a_2}{2}\right)^2 + y^2 + b_2y + \left(\frac{b_2}{2}\right)^2 = -c_2 + \left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 \]

E ottengo l'equazione in forma standard anche della seconda circonferenza.

\[ \left(x + \frac{a_2}{2}\right)^2 + \left(y + \frac{b_2}{2}\right)^2 = \left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 - c_2 \]

Dove ricavo immediatamente il centro e il raggio.

• Il centro della seconda circonferenza è $$ \left(-\frac{a_2}{2}, -\frac{b_2}{2}\right) $$
• Il raggio della seconda circonferenza è $$ r_1 = \sqrt{\left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 - c_2} $$

3] Confronto la distanza tra i centri con la differenza tra i raggi

A questo punto, una volta noti i centri e i raggi, posso verificare se una circonferenza è interna all'altra.

Calcolo la distanza tra i centri delle due circonferenze:

\[ d = \sqrt{\left(-\frac{a_1}{2} + \frac{a_2}{2}\right)^2 + \left(-\frac{b_1}{2} + \frac{b_2}{2}\right)^2} \]

Infine, confronto la somma dei raggi e la distanza tra i centri:

• Se \( d + r_1 \leq r_2 \), allora la prima circonferenza è interna alla seconda.
• Se \( d + r_2 \leq r_1 \), allora la seconda circonferenza è interna alla prima.

In alternativa, confronto la differenza assoluta dei raggi

• Se \( d \leq | r_1 - r_2 | \) e $ r_1<r_2 $, allora la prima circonferenza è interna alla seconda.
• Se \( d \leq | r_1 - r_2 | \) e $ r_1>r_2 $, allora la seconda circonferenza è interna alla prima.

Esempio

Considero le circonferenze con le seguenti equazioni:

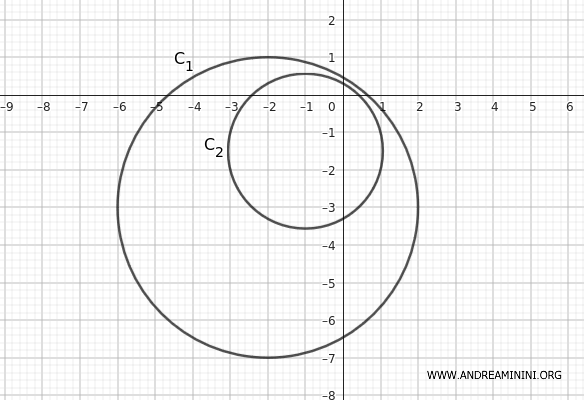
$$ C_1: x^2 + y^2 + 4x + 6y - 3 = 0 $$

$$ C_2: x^2 + y^2 + 2x + 3y - 1 = 0 $$

Completo i quadrati per trasformare le circonferenze nella loro forma standard.

Per \( C_1: x^2 + y^2 + 4x + 6y - 3 = 0 \):

$$ x^2 + 4x + y^2 + 6y = 3 $$

$$ (x^2 + 4x + 4) + (y^2 + 6y + 9) = 3 + 4 + 9 $$

$$ (x + 2)^2 + (y + 3)^2 = 16 $$

Nella forma standard è molto facile individuare il centro della circonferenza, in questo caso il centro di \( C_1 \) è $$(-2, -3) $$

Il raggio è invece $$  r_1 = \sqrt{16} = 4 $$

Spiegazione. Per completare il quadrato di $ x^2 + 4x $ devo aggiungere $ +4 $ in entrambi i lati dell'equazione. In questo modo ottengo $ x^2+ 4x + 4 = (x+2)^2 $ Allo stesso modo, per completare il quadrato di $ y^2 + 6x $ devo aggiungere $ +9 $ in entrambi i lati dell'equazione. In questo modo ottengo $ y^2+ 6y + 9 = (y+3)^2 $

Per \( C_2: x^2 + y^2 + 2x + 3y - 1 = 0 \):

$$ x^2 + 2x + y^2 + 3y = 1 $$

$$ (x^2 + 2x + 1) + (y^2 + 3y + \frac{9}{4}) = 1 + 1 + \frac{9}{4} $$

$$ (x + 1)^2 + \left(y + \frac{3}{2}\right)^2 = \frac{17}{4} $$

Quindi, il centro di \( C_2 \) è $$ (-1, -\frac{3}{2}) $$

Il raggio è invece

$$ r_2 = \sqrt{\frac{17}{4}} = \frac{\sqrt{17}}{2} \approx 2.06 $$

Una volta ottenute le coordinate dei centri \((-2, -3)\) e \((-1, -\frac{3}{2})\) e i raggi $ r_1 = 4 $ e $ r_2 = 2.06 $ delle due circonferenze, posso calcolare la distanza tra i centri e confrontarla con la differenza assoluta dei raggi

$$ d < | r_1 - r_2 | $$

La distanza (d) tra i centri \((-2, -3)\) e \((-1, -\frac{3}{2})\) è:

$$ d = \sqrt{(x_1 + x_2)^2 + (y_1 + y_2)^2} $$

$$ d = \sqrt{(-2 + 1)^2 + \left(-3 + \frac{3}{2}\right)^2} $$

$$  d = \sqrt{(-1)^2 + \left(-\frac{3}{2}\right)^2} $$

$$  d = \sqrt{1 + \frac{9}{4}} $$

$$  d = \sqrt{\frac{4}{4} + \frac{9}{4}} $$

$$  d = \sqrt{\frac{13}{4}} $$

$$  d = \frac{\sqrt{13}}{2} \approx 1.8 $$

Poi, verifico se una circonferenza è interna all'altra.

Confronto la differenza assoluta dei raggi e la distanza tra i centri:

$$ d < | r_1 - r_2 | $$

$$ 1.8 < | 4 - 2.06 | $$

$$ 1.8 < 1.94 $$

Questo conferma che una circonferenza è interna all'altra.

Poiché \( r_2 < r_1 \), posso concludere che la seconda circonferenza \( C_2 \) è interna alla prima circonferenza \( C_1 \).

Quindi, \( C_2 \) è interna a \( C_1 \).

Le circonferenze concentriche in geometria analitica

Due circonferenze concentriche hanno lo stesso centro ma raggio diverso. In geometria analitica, questo implica che le equazioni delle due circonferenze avranno gli stessi coefficienti $ a=a' $ e $ b=b' $ per i termini \( x \) e \( y \) ma diversi valori per il termine costante $ c \ne c' $.

Consideriamo le equazioni generali delle due circonferenze:

$$ C_1 :  x^2 + y^2 + ax + by + c = 0  $$

$$  C_2:  x^2 + y^2 + a'x + b'y + c' = 0  $$

Se le due circonferenze sono concentriche, hanno lo stesso centro.

Questo significa che i termini che coinvolgono \( x \) e \( y \) (cioè \( ax=a'x \) e \( by=b'y \)) devono essere identici in entrambe le equazioni.

Quindi, i coefficienti \( a \) e \( b \) devono essere uguali:

$$ a = a' $$

$$ b = b' $$

L'unica differenza tra due circonferenze concentriche è il termine costante \( c \), che rappresenta la differenza nei raggi delle circonferenze. Quindi, \( c \neq c' \).

$$ c \neq c' $$

Nota. Quando le equazioni delle due circonferenze hanno gli stessi coefficienti $ a=a' $, $ b=b' $ e $ c=c' $, allora le due circonferenze hanno lo stesso centro e lo stesso raggio, ovvero sono due circonferenze coincidenti.

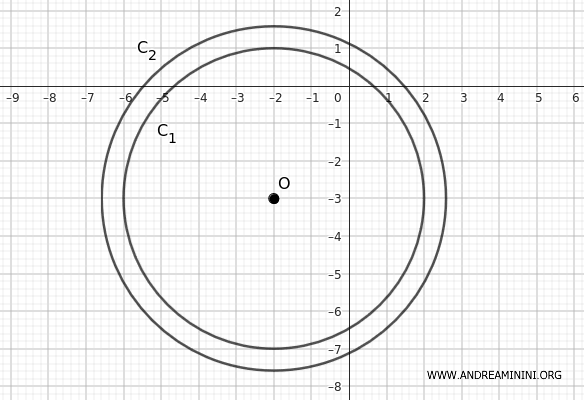
Esempio pratico

In questo esercizio considero le seguenti circonferenze:

$$ C_1 :  x^2 + y^2 + 4x + 6y - 3 = 0 $$

$$ C_2:   x^2 + y^2 + 4x + 6y - 8 = 0  $$

I centri delle circonferenze sono entrambi \( \left(-2, -3\right) \) poiché i coefficienti di \( x \) e \( y \) sono gli stessi.

$$ (x_o, y_0) = ( - \frac{a}{2} , -\frac{b}{2} ) = ( - \frac{4}{2} , -\frac{6}{2} ) = (-2, -3) $$

Sapendo che la formula per calcolare il raggio di una circonferenza è

$$ r = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2 - c} $$

I raggi delle due circonferenze sono i seguenti:

• Per la prima circonferenza: $$ r_1 = \sqrt{(-2)^2 + (-3)^2 + 3} = \sqrt{4 + 9 + 3} = \sqrt{16} = 4 $$
• Per la seconda circonferenza: $$ r_2 = \sqrt{(-2)^2 + (-3)^2 + 8} = \sqrt{4 + 9 + 8} = \sqrt{21} \approx 4.58 $$

La distanza tra i centri è zero d=0 perché sono concentriche e i raggi sono diversi, quindi le due circonferenze non sono coincidenti.

$$ d < | r_1 - r_2 | $$

$$ 0 < | 4 - 4.58 | $$

$$ 0 < 0.58 $$

Questo conferma che una circonferenza è interna all'altra.

Confrontando i raggi  \( r_1 = 4 \) e \( r_2 \approx 4.58 \) deduco che la prima circonferenza $ C_1 $, quella con il raggio inferiore (raggio 4), è interna alla seconda circonferenza $ C_2 $ (raggio circa 4.58).

 

E così via