Bisettrice di un angolo

La bisettrice di un angolo è una semiretta che ha origine nel vertice e divide l'angolo dato in due angoli congruenti, ossia di uguale ampiezza.

Ad esempio, considero un angolo di 60°

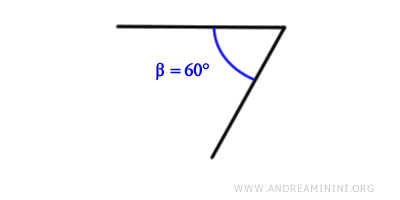
La bisettrice di quest'angolo è una semiretta che ha origine dal vertice e divide a metà l'angolo in due angoli di ampiezza pari a 30°

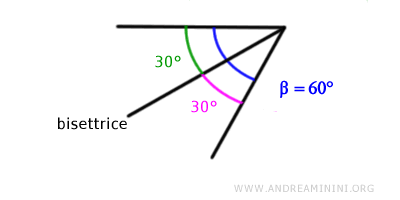
L'equazione della bisettrice

L'equazione che descrive le bisettrici degli angoli generati dall'intersezione di due rette è data da: $$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

Questa equazione descrive le due bisettrici risultanti dalla divisione di un angolo in due parti uguali.

Il simbolo ± riflette la presenza di due bisettrici distinte: una per l'angolo acuto e una per l'angolo ottuso, entrambi formati dall'incrocio delle due rette.

Esempio

Considero le seguenti equazioni di rette:

$$ r: \ x - y = 0 $$

$$ s: \ x + y - 4 = 0 $$

Sono due rette incidenti

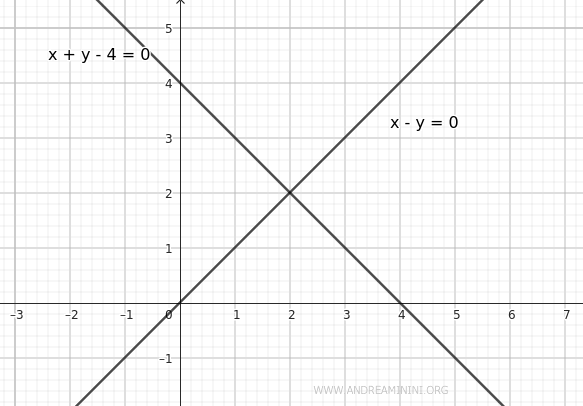
Utilizzo l'equazione generale delle bisettrici:

$$ \frac{ax + by + c}{\sqrt{a^2 + b^2}} = \pm \frac{a'x + b'y + c'}{\sqrt{a'^2 + b'^2}} $$

Sostituisco i coefficienti delle due equazioni: a=1, b=-1, c=0 e a'=1, b'=1, c=-4

$$ \frac{x -y }{\sqrt{1^2 + (-1)^2}} = \pm \frac{x + y -4}{\sqrt{1^2 + 1^2}} $$

$$ \frac{x -y }{\sqrt{1+1}} = \pm \frac{x + y -4}{\sqrt{1 + 1}} $$

$$ \frac{x -y }{\sqrt{2}} = \pm \frac{x + y -4}{\sqrt{2}} $$

Eliminiamo il denominatore \(\sqrt{2}\) poiché è uguale per entrambe le espressioni:

$$ \frac{x -y }{\sqrt{2}} \cdot \sqrt{2} = \pm \frac{x + y -4}{\sqrt{2}} \cdot \sqrt{2} $$

$$ x -y = \pm ( x + y -4 ) $$

Ora, separiamo i due casi per i segni:

• Per il segno positivo (+): $$ x - y = x + y - 4 $$ Riarrangio i termini $$ -2y = -4 $$ In questo caso l'equazione di una bisettrice è una retta parallela all'asse y $$ y = 2 $$
• Per il segno negativo (-): $$ x - y = -(x + y - 4) $$ $$ x - y = -x - y + 4 $$ Riarrangiando i termini: $$ 2x = 4 $$ L'altra bisettrice è una retta che, in questo caso, è parallela all'asse delle ascisse. $$ x = 2 $$

Quindi, le equazioni delle due bisettrici per gli angoli formati dalle rette sono $ y= 2 $ e $ x=2 $

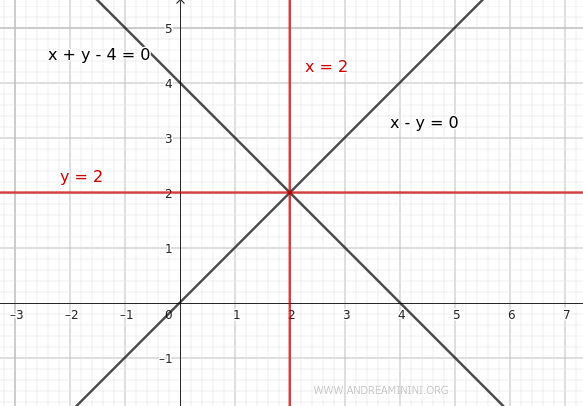
Osservazioni

Alcune osservazioni sulla bisettrice

• Per ogni angolo esiste una e una sola bisettrice.
• Due rette incidenti formano due coppie di angoli opposti congruenti e due bisettrici perpendicolari tra loro
  Ad esempio, se due rette r e s si intersecano formando un angolo acuto di 45°, l'angolo direttamente opposto sarà anch'esso di 45°. Poiché un angolo piatto ha un'ampiezza di 180°, l'angolo supplementare di 45° è un angolo ottuso di 135°, ovvero 180°-45°=135°, e anche il suo opposto è un angolo di 135°.
  
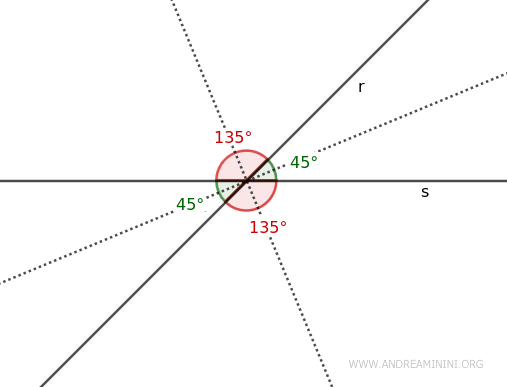
• Due angoli opposti al vertice hanno la stessa retta come bisettrice.
• I punti sulla bisettrice sono equidistanti dai lati dell'angolo
  La bisettrice di un angolo è un luogo geometrico perché un qualsiasi punto della bisettrice ha la stessa distanza dai lati dell'angolo.

  Dimostrazione. Considero un punto P qualsiasi della bisettrice r dell'angolo. Essendo la bisettrice gli angoli α≅α' sono congruenti. Traccio un segmento OP che unisce il vertice dell'angolo con il punto P sulla bisettrice e due segmenti perpendicolari ai lati dell'angolo AP e BP che hanno come estremo il punto P. Da queste premesse deduco che i triangoli sono congruenti OAP≡OBP per il secondo criterio di congruenza dei triangoli perché hanno due angoli congruenti e un lato congruente (OP). Essendo due triangoli congruenti, hanno tutti i lati congruenti. Quindi anche i lati AP≡BP sono congruenti. Questo dimostra che un qualsiasi punto P della bisettrice è equidistante dai lati dell'angolo.
  
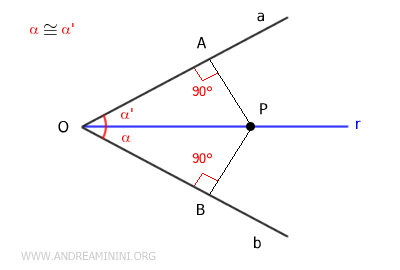
  Dimostrazione inversa. In questo caso devo dimostrare che un qualsiasi punto P equidistante dai lati dell'angolo è un punto della bisettrice. Per ipotesi iniziale, considero un punto P equidistante dai lati dell'angolo AP≡BP e una bisettrice r. La distanza di un punto da un segmento è la lunghezza del segmento perpendicolare al segmento che ha per estremo il punto P. Quindi, la distanza AP è perpendicolare rispetto al lato "a" mentre la distanza BP è perpendicolare rispetto al lato "b". I triangoli rettangolo OAP≡OBP sono congruenti per i criteri di congruenza dei triangolo rettangolo, perché i cateti AP≡BP e l'ipotenusa OP sono congruenti. Essendo congruenti, i due triangoli hanno tutti i lati e gli angoli congruenti. In particolar modo mi interessa sapere che gli angoli α≡α' dei triangoli OAP e OBP sono congruenti, perché questo vuol dire che l'ipotenusa OP e anche il punto P appartengono alla bisettrice r dell'angolo. Pertanto, se un punto P è equidistante dai lati di un angolo, allora è un punto della bisettrice r dell'angolo.

E così via.