Teorema della distanza di una retta dal centro di una circonferenza
Una retta è secante, tangente o esterna a una circonferenza se, rispettivamente, la sua distanza dal centro della circonferenza è minore, uguale o maggiore del raggio. E viceversa.
In altre parole, possono verificarsi tre situazioni:
Se una retta dista dal centro della circonferenza meno del raggio $ d<r $, allora è una retta secante alla circonferenza.
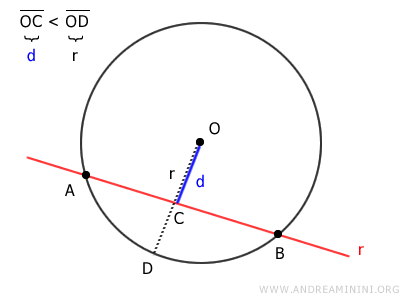
Se una retta tocca la circonferenza in un solo punto, la sua distanza dal centro è uguale al raggio $ d=r $, allora è una retta tangente alla circonferenza.
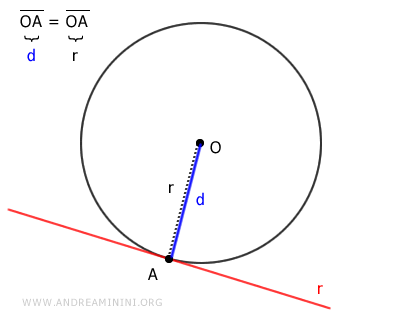
Infine, se la retta dista dal centro più del raggio $ d>r $ la retta non interseca affatto la circonferenza, quindi è una retta esterna alla circonferenza.
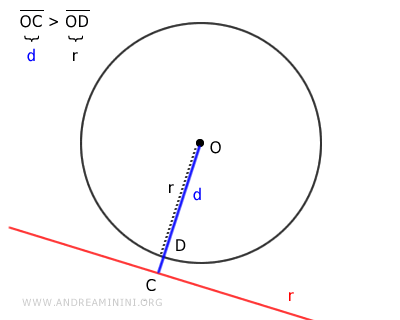
Vale anche il teorema inverso, quindi una retta secante, tangente o esterna ha rispettivamente una distanza minore, uguale o maggiore del raggio.
Come verificare i punti di intersezione in modo algebrico
In geometria analitica per capire se una retta è secante, tangente o esterna a una circonferenza, basta trovare le soluzioni di un sistema composto dall'equazione della circonferenza e dall'equazione della retta.
$$ \begin{cases} x^2 + y^2 + ax + bx+ c = 0 \\ \\ a'x+ b'y + c' = 0 \end{cases} $$
Le soluzioni x, y del sistema sono le coordinate (x;y) dei punti in comune tra la retta e la circonferenza.
Quindi, a seconda del numero di soluzioni possono verificarsi tre casi:
- 0 soluzioni: la retta è esterna alla circonferenza
- 1 soluzione: la retta è tangente
- 2 soluzioni: la retta è secante
Questo mi permette di ottenere il numero dei punti di intersezione in modo algebrico, senza dover rappresentare graficamente la retta e la circonferenza.
Un esempio pratico
Considero una circonferenza e una retta, devo capire se la retta è secante, tangente o esterna.
Non conosco il grafico della retta e della circonferenza, so soltanto quali sono le loro equazioni.
L'equazione della circonferenza è:
$$ x^2+y^2-6x-4y+4 =0 $$
L'equazione della retta è:
$$ x-y-4=0 $$
Metto entrambe le equazioni in un sistema
$$ \begin{cases} x^2+y^2-6x-4y+4 =0 \\ \\ x-y-4=0 \end{cases} $$
A questo punto devo verificare se il sistema di equazioni si può risolvere ed eventualmente quante sono le soluzioni.
Per risolvere il sistema applico il metodo della sostituzione, ricavo la y nella seconda equazione e sostituisco la variabile nella prima equazione.
$$ \begin{cases} x^2+(x-4)^2-6x-4 \cdot (x-4) +4 =0 \\ \\ y=x-4 \end{cases} $$
$$ \begin{cases} x^2+x^2-8x+16-6x-4x+16 +4 =0 \\ \\ y=x-4 \end{cases} $$
$$ \begin{cases} 2x^2-18x+36 =0 \\ \\ y=x-4 \end{cases} $$
La prima equazione può essere ulteriormente semplificata dividendo entrambi i lati per due.
$$ \begin{cases} x^2-9x+18 =0 \\ \\ y=x-4 \end{cases} $$
Studio il discriminante Δ della prima equazione.
$$ \Delta = b^2 - 4ac $$
$$ \Delta = (-9)^2 - 4 \cdot (1) \cdot (18) $$
$$ \Delta = 81 - 72 $$
$$ \Delta = 9 $$
Il discriminante è positivo, quindi il sistema ha due soluzioni e già posso affermare che la retta è secante alla circonferenza perché la interseca in due punti.
Nota. Lo studio del segno del discriminante mi permette di sapere subito il numero delle soluzioni della prima equazione del sistema. A seconda del valore di Δ:
- Se Δ>0 l'equazione ha due soluzioni reali distinte, quindi la retta è secante alla circonferenza.
- Se Δ=0 l'equazione ha una soluzione reale doppia, quindi la retta è tangente alla circonferenza.
- Se Δ<0 l'equazione non ha soluzioni reali, quindi la retta è esterna alla circonferenza.
Quali sono le coordinate dei punti di intersezione?
A questo punto, poiché il discriminante non è negativo (il caso della retta esterna), posso calcolare con precisione le coordinate (x;y) dei punti di intersezione.
Calcolo le soluzioni dell'equazione $ x^2-9x+18 =0 $
$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$
$$ x = \frac{-(-9) \pm \sqrt{ 9}}{2 \cdot 1} $$
$$ x = \frac{9 \pm 3}{2} = \begin{cases} x = \frac{9-3}{2} = 3 \\ \\ x = \frac{9+3}{2} = 6 \end{cases} $$
Quindi, la prima equazione del sistema ha due soluzioni in x=3 e x=6.
$$ \begin{cases} 2x^2-18x+36 =0 \\ \\ y=x-4 \end{cases} $$
Sostituisco i valori della x nella seconda equazione del sistema per trovare i valori corrispondenti della y.
$$ y = x - 4 = \begin{cases} y=3-4 = -1 \\ \\ y=6-4 = 2 \end{cases} $$
La prima soluzione del sistema è la coppia di valori x=3 e y=-1.
La seconda soluzione è la coppia di valori x=6 e y=2.
Pertanto, la retta ha due punti di intersezione con la circonferenza in (3;-1) e (6;2).
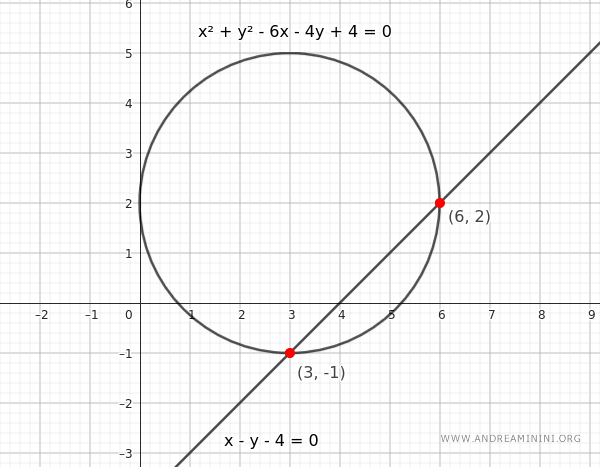
In conclusione, questo metodo permette di determinare algebricamente la posizione relativa della retta rispetto alla circonferenza senza dover ricorrere alla rappresentazione grafica.
La dimostrazione
La dimostrazione si sviluppa in tre casi
A] Distanza della retta minore del raggio
Considero una retta r e una circonferenza con centro O e raggio OA.
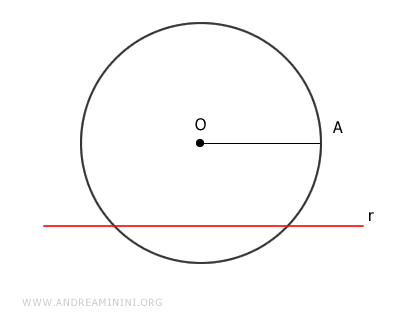
La distanza della retta dal centro O della circonferenza è il segmento OB.
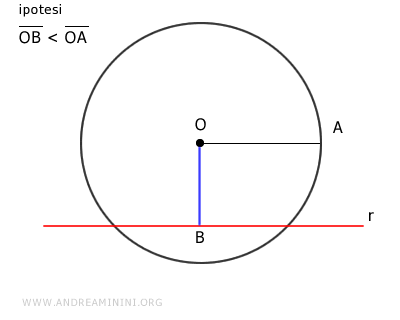
Per ipotesi iniziale la distanza della retta dal centro della retta è minore del raggio.
$$ \overline{OB} < \overline{OA} $$
Sulla retta r traccio un segmento BC con il raggio OA
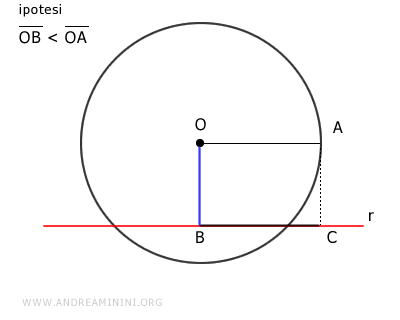
Traccio un segmento OC che congiunge il punto C con il centro della circonferenza.
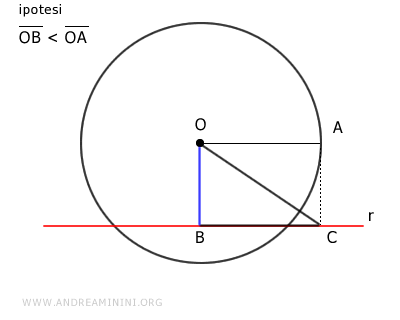
In questo modo ottengo un triangolo rettangolo OBC.
Poiché è un triangolo rettangolo, deduco che l'ipotenusa OC è maggiore dei singoli cateti OB e BC.
In particolar modo mi interessa sapere che OC>BC
$$ \overline{OC} > \overline{BC} $$
Sapendo che BC≅OA è congruente con il raggio (OA), deduco che il segmento OC è maggiore del raggio.
$$ \overline{OC} > \overline{OA} $$
Quindi, il punto C è un punto esterno alla circonferenza.
Il segmento BC ha un punto interno (B) e un punto esterno (C) alla circonferenza come estremi.
Pertanto, BC interseca la circonferenza almeno in un punto D.
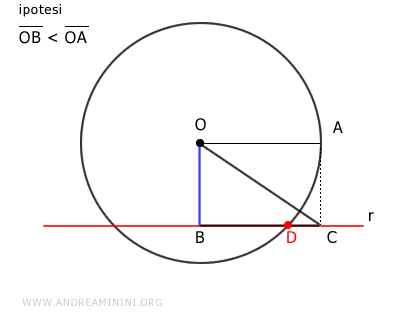
Ripeto lo stesso procedimento nella semiretta opposta.
Sulla retta r traccio un segmento BE congruente con il raggio OA della circonferenza.
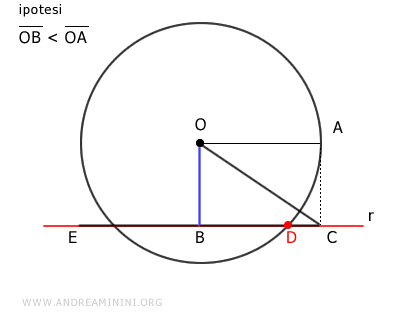
Poi traccio il segmento OE in modo da ottenere un triangolo rettangolo OBE.
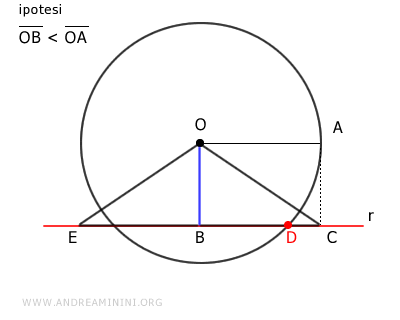
Anche in questo caso l'ipotenusa OE è maggiore dei cateti OB e EB.
$$ \overline{OE} > \overline{EB} $$
Il segmento EB ha un punto interno (B) e un punto esterno (E) della circonferenza come estremi.
Quindi, EB interseca la circonferenza in almeno un punto F.
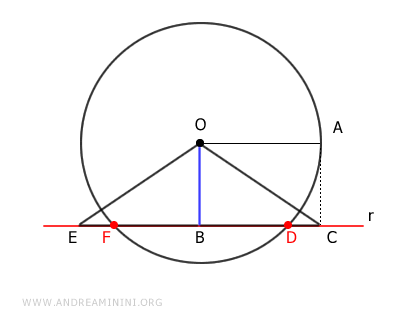
Questo dimostra che la retta r interseca la circonferenza in due punti distinti D e F.
Quindi, la retta r è una retta secante alla circonferenza.
B] Distanza della retta uguale al raggio
In questo caso, per ipotesi iniziale la retta r ha una distanza dal centro O della circonferenza uguale al raggio OA.
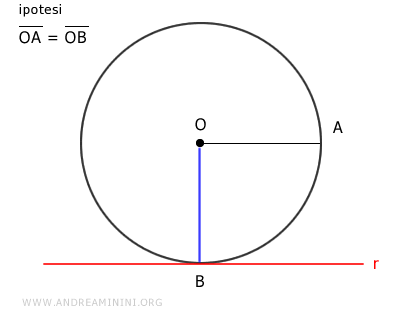
Quindi, l'ipotesi iniziale è OB=OA
$$ \overline{OB} = \overline{OA} $$
Sulla retta r traccio un segmento BC congruente con il raggio OA ossia BC≅OA
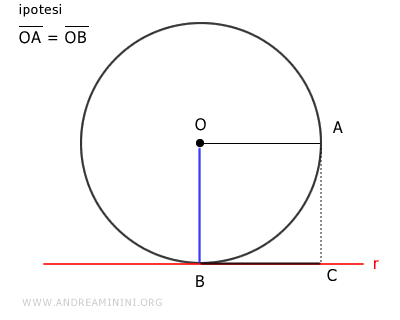
Poi congiungo i punti O e C.
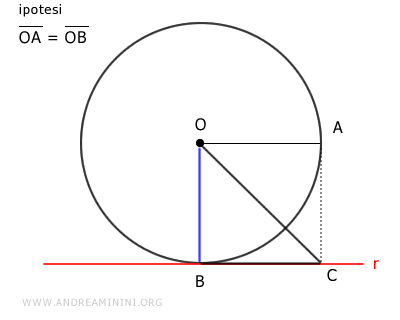
Il triangolo OBC è un triangolo rettangolo.
In un triangolo rettangolo l'ipotenusa è sempre maggiore dei singoli cateti. Quindi OC>BC.
$$ \overline{OC} > \overline{BC} $$
A sua volta, essendo BC≅OA congruente con il raggio, il segmento BC è maggiore del raggio ossia OC>BA
$$ \overline{OC} > \overline{OA} $$
Da questo deduco che il punto C è un punto esterno alla circonferenza.
Quindi, il segmento BC ha un punto interno (B) e un punto esterno (C) della circonferenza come estremi.
Questo vuol dire che interseca la circonferenza in almento un punto (B)
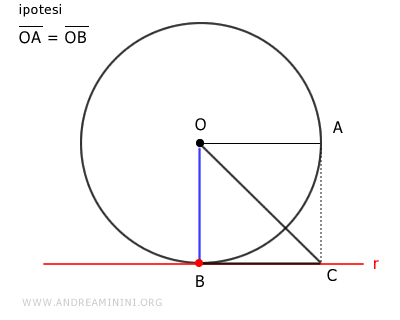
Ripeto lo stesso procedimento dall'altra parte.
Costruisco un segmento BD sulla retta r dove BD≅OA è congruente con il raggio della circonferenza.
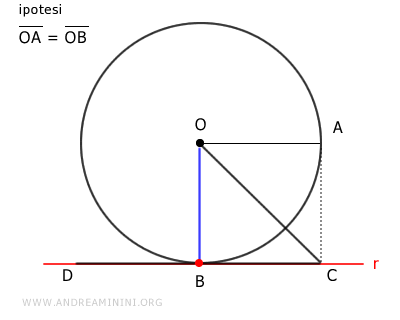
Poi congiungo i punti O e D
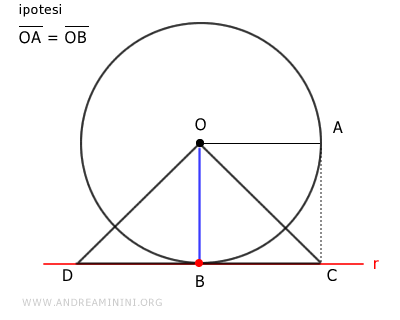
Il triangolo OBD è un triangolo rettangolo.
Quindi, l'ipotenusa OD è maggiore del cateto BD
$$ \overline{OD} > \overline{BD} $$
Di consequenza, il segmento OB è maggiore anche del raggio OA poiché BD≅OA per costruzione.
$$ \overline{OD} > \overline{OA} $$
Da questo deduco che il punto D è un punto esterno della circonferenza.
Il segmento BD ha un punto interno (B) e un punto esterno (D) della circonferenza come estremi. Quindi, deve intersecare la circonferenza in almento un punto B.

In questo caso il punto di intersezione è ancora B.
Questo significa che la retta r interseca la circonferenza in un solo punto.
Pertanto, la retta r è una retta tangente alla circonferenza.
C] Distanza della retta maggiore al raggio
In questo caso l'ipotesi iniziale è che la retta r abbia una distanza (OB) dal centro O della circonferenza maggiore del raggio (OA).
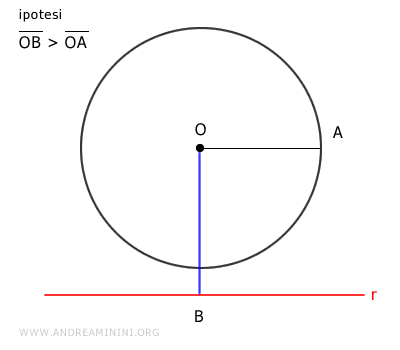
Quindi, l'ipotesi iniziale è
$$ \overline{OB} > \overline{OA} $$
La distanza tra un punto e una retta è rappresentata dal segmento perpendicolare più corto che congiunge il punto alla retta.
Se questa distanza supera il raggio, allora nessun altro segmento che congiunge il punto O a un qualsiasi punto C della retta può avere una lunghezza minore.
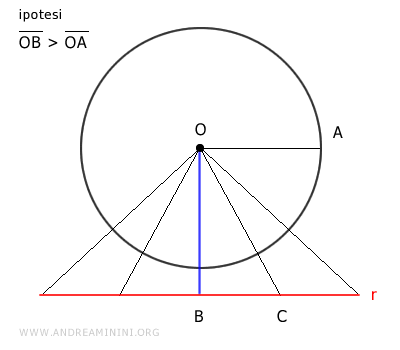
Questo si dimostra facilmente considerando che qualsiasi altro punto C della retta forma un triangolo rettangolo OBC in cui il segmento OC è l'ipotenusa.
In un triangolo rettangolo l'ipotenusa è sempre maggiore di ogni singolo cateto, quindi OC>OB in qualsiasi situazione.
$$ \overline{OC} > \overline{OB} $$
Sapendo che OB>OA è maggiore del raggio della circonferenza per l'ipotesi iniziale, deduco che anche OC è maggiore del raggio OA.
$$ \overline{OC} > \overline{OB} > \overline{OA} $$
Pertanto, ogni punto della retta r è un punto esterno alla circonferenza. Non ci sono punti in comune.
Di conseguenza, la retta r è una retta esterna alla circonferenza.
Il teorema inverso
La distanza di una retta dal centro di una circonferenza è minore, uguale o maggiore del raggio, se, rispettivamente, la retta è secante, tangente o esterna alla circonferenza.
La dimostrazione
Per dimostrare il teorema inverso, procedo per assurdo.
Suppongo per ipotesi che una retta tangente a una circonferenza non abbia una distanza dal centro pari al raggio.
Esistono due scenari da considerare:
- La distanza è minore del raggio
In questo caso, ci sono due punti distinti in cui la retta interseca la circonferenza. Questo significherebbe che la retta è sia secante sia tangente, il che è logicamente impossibile.

- La distanza è maggiore del raggio
In questa situazione, la retta non tocca la circonferenza in alcun punto. Tuttavia, questo contraddice la definizione di tangente, che deve toccare la circonferenza esattamente in un punto.

Da queste contraddizioni, concludo che l'ipotesi iniziale è errata. Pertanto, è vero il suo contrario.
In conclusione, posso affermare con certezza che una retta tangente ha una distanza dal centro della circonferenza uguale al raggio.
E così via.
