La formula del raggio di una circonferenza
Per trovare il raggio di una circonferenza con l'equazione scritta nella forma generale $$ x^2 + y^2 + Dx + Ey + F = 0 $$ utilizzo questa formula $$ r = \sqrt{ (-\frac{D}{2})^2 + ( -\frac{E}{2} )^2 - F } $$
Se l'equazione della circonferenza è scritta nella forma standard, trovare il raggio è molto più semplice
\[ (x - h)^2 + (y - k)^2 = r^2 \]
In questo caso il centro e il raggio della circonferenza sono:
- \( (h, k) \) sono le coordinate del centro della circonferenza
- \( r \) è il raggio della circonferenza.
Quando, invece, l'equazione della circonferenza è scritta nella forma generale
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
Il centro \((h, k)\) della circonferenza si trova usando le seguenti formule:
$$ h = -\frac{D}{2} $$
$$ k = -\frac{E}{2} $$
Dove \(D\) e \(E\) sono i coefficienti delle variabili \(x\) e \(y\) nell'equazione generale $ x^2 + y^2 + Dx + Ey + F = 0 $ della circonferenza.
Pertanto, il centro della circonferenza si trova alle coordinate \((-D/2, -E/2)\).
Il raggio della circonferenza si trova usando questa formula:
$$ r = \sqrt{ (-\frac{D}{2})^2 + ( -\frac{E}{2} )^2 - F } $$
In alternativa, per trovare il raggio e il centro di una circonferenza posso trasformare l'equazione dalla forma generale alla forma standard, completando il quadrato e aggiungendo i termini necessari. Nella forma generale $ (x - h)^2 + (y - k)^2 = r^2 $ il raggio si calcola semplicemente tramite la radice quadrata $ r = \sqrt{r^2} $
Un esempio pratico
Esempio 1
In questo esempio ho l'equazione standard della circonferenza:
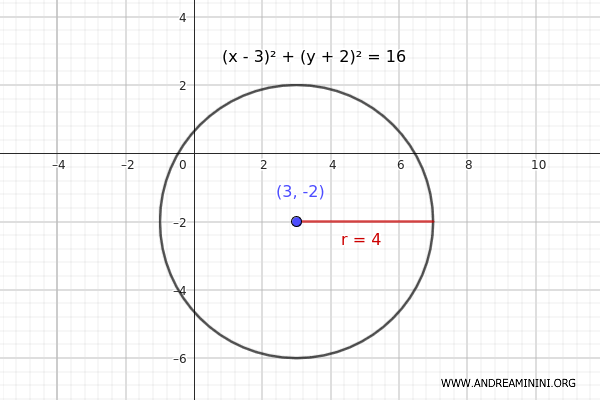
$$ (x - 3)^2 + (y + 2)^2 = 16 $$
Pertanto, trovare il raggio e il centro è molto semplice.
- Il centro della circonferenza è \( (3, -2) \).
- Il termine a destra dell'uguale è \( r^2 = 16 \).
Per trovare il raggio \( r \) mi basta calcolare la radice quadrata positiva di 16:
$$ r = \sqrt{16} = 4 $$
Quindi, il raggio della circonferenza è 4.
Esempio 2
In questo esercizio l'equazione della circonferenza non è in forma standard.
$$ x^2 + y^2 + 6x - 8y + 9 = 0 $$
In questo caso, per trovare il raggio posso usare la formula del raggio:
$$ r = \sqrt{ (-\frac{D}{2})^2 + ( -\frac{E}{2} )^2 - C } $$
Dove i coefficienti dell'equazione generale $ x^2 + y^2 + Dx + Ey + F = 0 $ sono D=6, E=-8 e C=9.
$$ r = \sqrt{ (-\frac{6}{2})^2 + ( -\frac{-8}{2} )^2 - 9 } $$
$$ r = \sqrt{ (-3)^2 + (4)^2 - 9 } $$
$$ r = \sqrt{ 9 + 16 - 9 } $$
$$ r = \sqrt{ 16 } $$
$$ r = 4 $$
In alternativa, posso trovare il raggio trasformando l'equazione generale della circonferenza nella forma standard.
Raggruppo i termini \( x \) e \( y \)
$$ x^2 + y^2 + 6x - 8y + 9 = 0 $$
$$ (x^2 + 6x) + (y^2 - 8y) = -9 $$
Completo il quadrato per \( x \) aggiungendo e sottraendo il termine $ ( \frac{6}{2})^2 $
$$ (x^2 + 6x +(\frac{6}{2})^2) - (\frac{6}{2})^2 + (y^2 - 8y) = -9 $$
$$ (x^2 + 6x +3^2) - 3^2 + (y^2 - 8y) = -9 $$
$$ (x + 3)^2 - 9 + (y^2 - 8y) = -9 $$
$$ (x + 3)^2 + (y^2 - 8y) = 0 $$
Completo il quadrato per \( y \) aggiungendo e sottraendo il termine $ ( \frac{8}{2})^2 $
$$ (x + 3)^2 + (y^2 - 8y + (\frac{8}{2})^2 ) - (\frac{8}{2})^2 =0 $$
$$ (x + 3)^2 + (y^2 - 8y + 4^2 ) - 4^2 =0 $$
$$ (x + 3)^2 + (y-4)^2 = 4^2 $$
$$ (x + 3)^2 + (y-4)^2 = 16 $$
Ora l'equazione è nella forma standard e il termine a destra dell'uguale è \( r^2 = 16 \).
Per calcolare il raggio mi basta trovare la radice quadrata di questo termine:
$$ r = \sqrt{16} = 4 $$
Quindi, il raggio della circonferenza è 4.
Altre formule utili per trovare il raggio
In generale, la formula per trovare il raggio \( r \) di una circonferenza dipende dalle informazioni a mia disposizione.
Ecco alcune situazioni comuni:
- Se conosco la lunghezza della circonferenza $$ r = \frac{C}{2\pi} $$ dove \( C \) è la lunghezza della circonferenza.
- Se conosco l'area della circonferenza $$ r = \sqrt{\frac{A}{\pi}} $$ dove \( A \) è l'area della circonferenza.
- Se conosco le coordinate dei due punti estremi \( (x_1, y_1) \) e \( (x_2, y_2) \) che formano il diametro della circonferenza, il raggio è metà della distanza euclidea tra questi due punti: $$ r = \frac{\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}}{2} $$
Queste formule mi permettono di calcolare il raggio di una circonferenza in diverse situazioni. Le aggiungo per completezza.
E così via.
