Le circonferenze secanti

Due circonferenze sono circonferenze secanti quando hanno due punti in comune.

Le circonferenze non possono intersecarsi in più di due punti perché in tre punti passa una e una sola circonferenza.

Quindi, se avessero tre punti in comune le due circonferenze coinciderebbero.

Teorema delle circonferenze secanti

La condizione necessaria e sufficiente affinché due circonferenze siano secanti è che la distanza dei centri sia minore della somma dei raggi e maggiore della loro differenza. $$ | r-r' | < OO' < r+r' $$

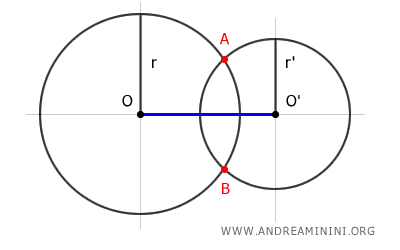
Dimostrazione

Per dimostrarlo basta tracciare il segmento OO' tra i due centri della circonferenza e il raggio di ciascuna circonferenza verso lo stesso punto secante (ad esempio il punto A).

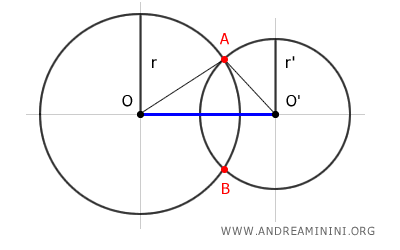
I segmenti formano un triangolo OO'A.

Per il teorema della disuguaglianza triangolare, ogni lato del triangolo è minore della somma degli altri due lati e maggiore della differenza degli altri due lati.

Quindi, il segmento OO' che congiunge i due centri delle circonferenze deve essere minore rispetto alla somma dei raggi delle due circonferenze (r+r') e minore rispetto alla loro differenza (r-r').

Come trovare in punti di intersezione

Per trovare i punti di intersezione di due circonferenze secanti bisogna utilizzare la geometria analitica.

Se considero due circonferenze con centri \((x_1, y_1)\) e \((x_2, y_2)\) e raggi \(r_1\) e \(r_2\):

Le equazioni delle due circonferenze sono:

\[ (x - x_1)^2 + (y - y_1)^2 = r_1^2 \]

\[ (x - x_2)^2 + (y - y_2)^2 = r_2^2 \]

Ecco i passaggi generali per trovare i punti di intersezione di due circonferenze

1. Metto le equazioni delle due circonferenze in un sistema e lo risolvo passo passo: \[ \begin{cases} x^2 + y^2 - 2x_1x - 2y_1y + x_1^2 + y_1^2 = r_1^2 \\ x^2 + y^2 - 2x_2x - 2y_2y + x_2^2 + y_2^2 = r_2^2 \end{cases} \]
2. Sottraggo una equazione dall'altra. Ad esempio, la seconda dalla prima per eliminare i termini \(x^2\) e \(y^2\). In questo modo una delle due equazioni diventa lineare.
3. Risolvo l'equazione lineare per una delle variabili, ad esempio \( y \) in termini di \( x \)
4. Sostituiscol'espressione trovata per \( y \) nell'equazione di una delle circonferenze (di solito la più semplice)
5. Risolvo l'equazione quadratica per \( x \) usando la formula quadratica: \[ ax^2 + bx + c = 0 \] \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
6. Una volta trovati i valori di \( x \), li sostituisco nell'espressione per \( y \) per ottenere i valori corrispondenti di \( y \).

In generale, questi passaggi mi consentono di ottenere le coordinate (x;y) dei due punti di intersezione delle circonferenze secanti.

Esempio

Considero due circonferenze secanti le cui equazioni sono:

$$  C_1 : \ x^2 + y^2 = 25 $$

$$ C_2 : \ (x - 4)^2 + (y - 3)^2 = 16 $$

La prima equazione rappresenta una circonferenza con centro nell'origine degli assi O(0;0) e raggio uguale a $ r_1 = 5 $.

La seconda equazione, invece, è una circonferenza con il centro nel punto (4;3) e un raggio pari a $ r_2 = 4 $.

La distanza euclidea tra i centri OO' alle coordinate (x₁;y₁) e (x₂;y₂) è $ d=5 $

$$ d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} $$

$$ d = \sqrt{(0-4)^2+(0-3)^2} $$

$$ d = \sqrt{16+9} = \sqrt{25} = 4 $$

Secondo il teorema, quando due circonferenze sono secanti la distanza tra due centri (d=4) è inferiore alla somma dei raggi e superiore al valore assoluto della differenza dei raggi.

$$ | r_1-r_2 | < d < r_1+r_2 $$

$$ | 5-4 | < 4 < 5+4 $$

$$ 1 < 4 < 9 $$

Quindi, le due circonferenze sono effettivamente due circonferenze secanti.

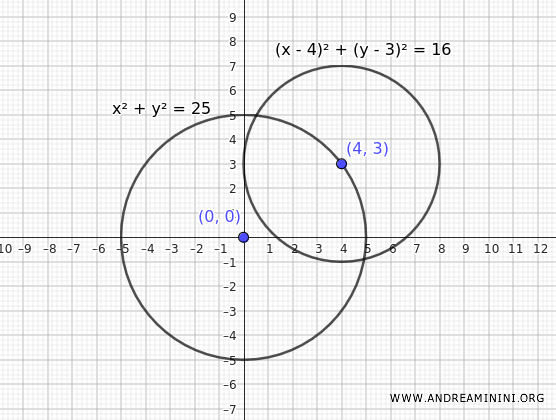
Quali sono i punti di intersezione delle due circonferenze?

Espando la seconda equazione:

\[ (x - 4)^2 + (y - 3)^2 = 16 \]

\[ (x^2 - 8x + 16) + (y^2 - 6y + 9) = 16 \]

\[ x^2 + y^2 - 8x - 6y + 25 = 16 \]

\[ x^2 + y^2 - 8x - 6y + 9 = 0 \]

A questo punto costruisco il sistema di equazioni:

\[ \begin{cases} x^2 + y^2 = 25 \\ x^2 + y^2 - 8x - 6y + 9 = 0 \end{cases} \]

Sottraggo la prima equazione dalla seconda:

\[ \begin{cases} x^2 + y^2 = 25 \\ (x^2 + y^2 - 8x - 6y + 9) - (x^2 + y^2) = 0 - 25 \end{cases} \]

\[ \begin{cases} x^2 + y^2 = 25 \\ - 8x - 6y + 9 = -25 \end{cases} \]

\[ \begin{cases} x^2 + y^2 = 25 \\  -8x - 6y = -34 \end{cases} \]

Moltiplico per -1 entrambi i lati della seconda equazione per trasformare i valori negativi in positivi e semplificare i calcoli

\[ \begin{cases} x^2 + y^2 = 25 \\  8x + 6y = 34 \end{cases} \]

\[ \begin{cases} x^2 + y^2 = 25 \\   4x + 3y = 17 \end{cases} \]

Quindi, posso risolvere per \( y \) in termini di \( x \):

\[ \begin{cases} x^2 + y^2 = 25 \\   y = \frac{17 - 4x}{3} \end{cases} \]

Sostituisco \( y \) nella prima equazione:

\[ \begin{cases} x^2 + \left( \frac{17 - 4x}{3} \right)^2 = 25 \\   y = \frac{17 - 4x}{3} \end{cases} \]

\[ \begin{cases} x^2 + \frac{(17 - 4x)^2}{9} = 25 \\   y = \frac{17 - 4x}{3} \end{cases} \]

\[ \begin{cases} 9x^2 + (17 - 4x)^2 = 225 \\   y = \frac{17 - 4x}{3} \end{cases} \]

\[ \begin{cases} 9x^2 + 289 - 136x + 16x^2 = 225 \\   y = \frac{17 - 4x}{3} \end{cases} \]

\[ \begin{cases} 25x^2 - 136x + 289 = 225 \\   y = \frac{17 - 4x}{3} \end{cases} \]

\[ \begin{cases} 25x^2 - 136x + 64 = 0 \\   y = \frac{17 - 4x}{3} \end{cases} \]

Risolvo questa equazione quadratica: 25x² - 136x + 64 = 0

\[ x = \frac{136 \pm \sqrt{136^2 - 4 \cdot 25 \cdot 64}}{2 \cdot 25} \]

\[ x = \frac{136 \pm \sqrt{18496 - 6400}}{50} \]

\[ x = \frac{136 \pm \sqrt{12096}}{50} \]

\[ x = \frac{136 \pm 110}{50} \]

In questo modo trovo i valori delle componenti x dei punti di intersezione

\[ x = \frac{136 + 110}{50} = \frac{246}{50} = 4.92 \]

\[ x = \frac{136 - 110}{50} = \frac{26}{50} = 0.52 \]

Infine, sapendo che

$$ y = \frac{17 - 4x}{3}  $$

trovo i valori corrispondenti delle componenti \( y \):

• Per \( x = 4.92 \): \[ y = \frac{17 - 4 \cdot 4.92}{3} = \frac{17 - 19.68}{3} = \frac{-2.68}{3} = -0.893 \]
• Per \( x = 0.52 \): \[ y = \frac{17 - 4 \cdot 0.52}{3} = \frac{17 - 2.08}{3} = \frac{14.92}{3} = 4.973 \]

Pertanto, i punti di intersezione sono quindi approssimativamente alle coordinate \( (4.92, -0.893) \) e  \( (0.52, 4.973) \)

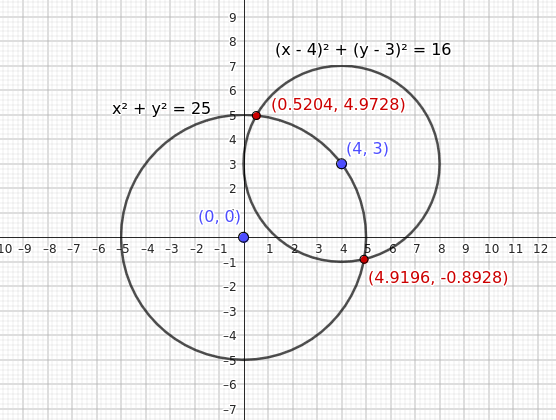
Questi sono i punti di intersezione delle due circonferenze secanti.

Osservazioni

Alcune osservazioni sulle circonferenze secanti

• La corda AB che congiunge i due punti di intersezione delle circonferenze secanti è perpendicolare al segmento OO' tra i centri delle due circonferenze.
  

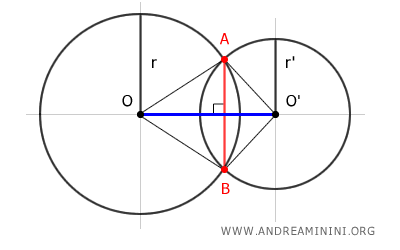
  La dimostrazione. Considero due circonferenze secanti nei punti A e B. Traccio il segmento OO' che congiunge i due centri delle circonferenze O e O'. Traccio i segmenti OA, OB, O'A e O'B. I segmenti OA≅OB sono congruenti perché corrispondono a due raggi della prima circonferenza. $$ \overline{OA} \cong \overline{OB} $$ Allo stesso modo i segmenti O'A≅O'B sono congruenti perché corrispondono a due raggi della seconda circonferenza. $$ \overline{O'A} \cong \overline{O'B} $$ Quindi, i punti A e B sono equidistanti sia dal centro O che dal centro O', questo vuol dire che la corda AB è perpendicolare al segmento OO'.

E così via.