Fasci di circonferenze

I fasci di circonferenze sono insiemi di circonferenze che condividono alcune proprietà comuni.

Ce ne sono principalmente due tipi: fascio proprio e fascio improprio.

• Fascio proprio
  Le circonferenze passano tutte per due punti fissi, detti punti base. L'equazione generale di un fascio proprio è del tipo \( \lambda (x^2 + y^2) + \mu (Ax + By + C) = 0 \), dove \( \lambda \) e \( \mu \) sono parametri.
• Fascio improprio
  Le circonferenze hanno tutte lo stesso centro e variano solo per il raggio. L'equazione di un fascio improprio è del tipo \( (x - h)^2 + (y - k)^2 = r^2 \), con \( (h, k) \) centro comune e \( r \) che varia.

Il fascio di circonferenze di due circonferenze generatrici

Il fascio di circonferenze è l'insieme di tutte le circonferenze generate dalla combinazione lineare di due circonferenze generatrici. $$ (x^2+y^2+ax+by+c) + k \cdot ( x^2+y^2+a'x+b'y+c' )  = 0  $$ Dove k è un valore intero qualsiasi.

Questa equazione del fascio di circonferenze generata tutte le circonferenze del fascio al variare del parametro k, tranne la seconda circonferenza generatrice perché nessun valore di k può generarla.

Ci sono però due casi particolari che è utile analizzare nel dettaglio.

• Se k=0 si ottiene la prima circonferenza $$ (x^2+y^2+ax+by+c) + k \cdot ( x^2+y^2+a'x+b'y+c' )  = 0  $$ $$ (x^2+y^2+ax+by+c) + 0 \cdot ( x^2+y^2+a'x+b'y+c' )  = 0  $$ $$ x^2+y^2+ax+by+c = 0  $$
• Se k=-1 si ottiene una retta detta asse radicale del fascio di circonferenze $$ (x^2+y^2+ax+by+c) + k \cdot (x^2+y^2+a'x+b'y+c') = 0 $$$$ (x^2+y^2+ax+by+c) + (-1) \cdot (x^2+y^2+a'x+b'y+c') = 0 $$ $$ \require{cancel} \cancel{x^2}+\cancel{y^2}+ax+by+c - \cancel{x^2}-\cancel{y^2}-a'x-b'y-c' = 0 $$ $$ (a-a')x+(b-b')y+c-c' = 0 $$ 

Nota. L'asse radicale del fascio di circonferenze è una "circonferenza degenere" perché posso considerarla come una circonferenza di raggio infinito.

L'asse radicale del fascio di circonferenze può intersecare o meno le due generatrici

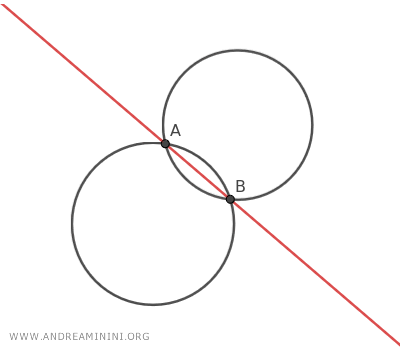
• Se le generatrici si intersecano in due punti A e B, detti punti base del fascio, l'asse radicale passa per entrambi i punti.
  
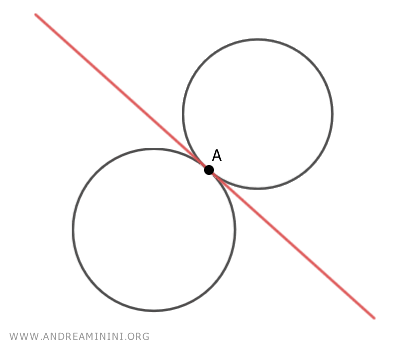
• Se le generatrici sono tangenti in un unico punto base A, l'asse radicale passa per il punto di tangenza delle due circonferenze generatrici
  
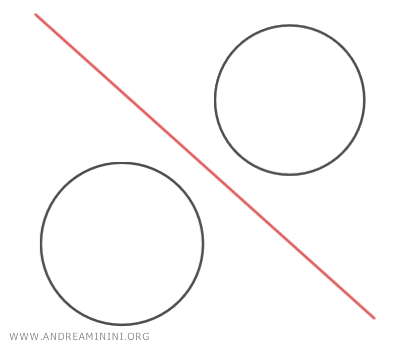
• Se le generatrici sono esterne, ovvero non hanno punti in comune, l'asse radicale passa nello spazio esterno tra le due generatrici.
  

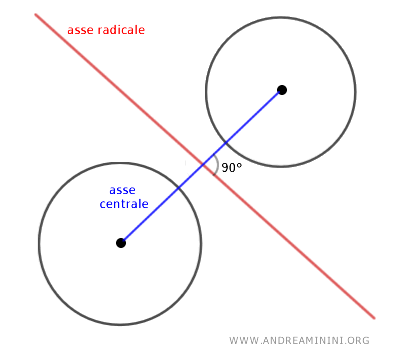
Il luogo geometrico composto da tutti i centri delle circonferenze generate in un fascio di circonferenza è un asse perpendicolare all'asse radicale detto asse centrale del fascio.

Nota. Nel caso particolare in cui i coefficienti a=a' e b=b' sono uguali, le due circonferenze generatrici sono concentriche. In questo caso il fascio di circonferenze è composto esclusivamente da circonferenze concentriche e l'asse radicale non esiste.

Esempio

Considero due circonferenze generatrici

$$ C_1 : \ x^2+y^2+2x+3y-5=0 $$

$$ C_2 : \ x^2+y^2-4x-4y+1=0 $$

Queste due circonferenze si intersecano in due punti base A e B.

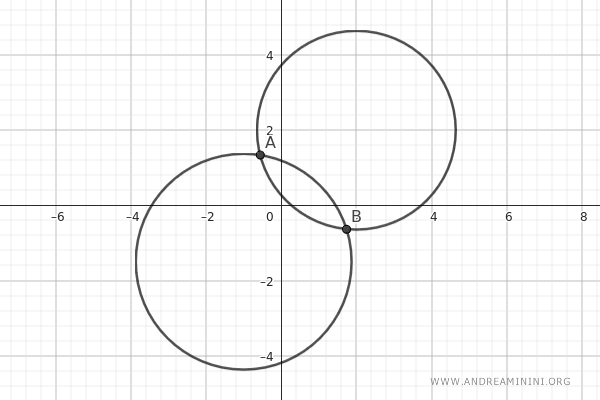
Questo vuol dire che tutte le circonferenze del fascio di circonferenze passeranno per questi due punti A e B.

L'equazione del fascio di circonferenze delle due generatrici è la seguente:

$$ C_1 + k \cdot C_2 = 0 $$

$$ (x^2+y^2+2x+3y-5) + k \cdot (x^2+y^2-4x-4y+1) = 0 $$

Al variare del parametro k ottengo tutte le circonferenze del fascio.

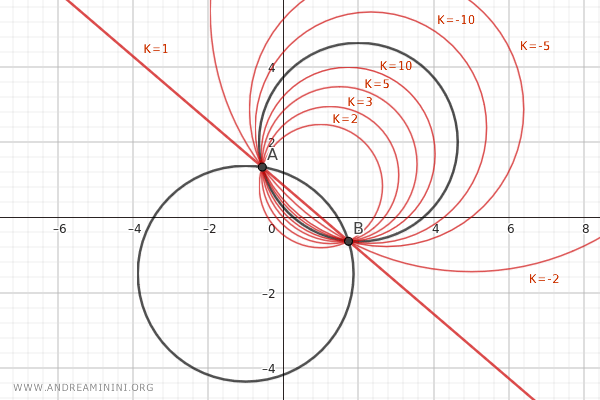
Nel caso in cui k=0 si ottiene la circonferenza C₁

$$ (x^2+y^2+2x+3y-5) + 0 \cdot (x^2+y^2-4x-4y+1) = 0 $$

$$ x^2+y^2+2x+3y-5 = 0 $$

Nel caso in cui k=-1 si ottiene l'asse radicale delle circonferenze che passa per entrambi i punti base A e B del fascio di circonferenze.

$$ (x^2+y^2+2x+3y-5) + (-1) \cdot (x^2+y^2-4x-4y+1) = 0 $$

$$ \require{cancel} \cancel{x^2}+\cancel{y^2}+2x+3y-5 - \cancel{x^2}-\cancel{y^2}+4x+4y-1 = 0 $$

$$ (2+4)x+(3+4)y-5-1 = 0 $$ $$ 6x+7y-6 = 0 $$

L'asse centrale del fascio di circonferenze è la retta che passa per tutti i centri delle circonferenze del fascio ed è perpendicolare all'asse radicale.

 

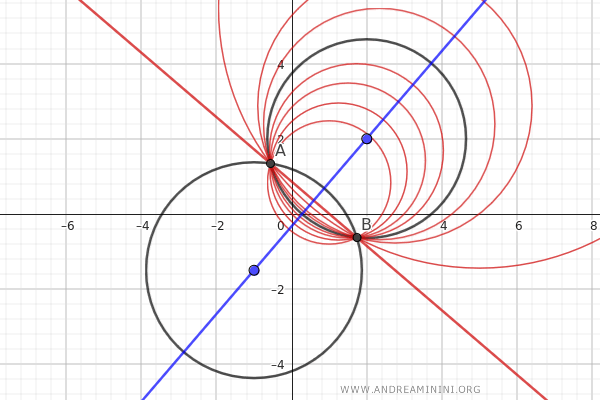
La dimostrazione

Considero due circonferenze generatrici:

$$ C_1 = x^2+y^2+ax+by+c= 0 $$

$$ C_2 = x^2+y^2+a'x+b'y+c'= 0 $$

Calcolo la combinazione lineare delle due circonferenze dove h e j sono due numeri interi qualsiasi:

$$ h \cdot C_1 + j \cdot C_2 = 0 $$

$$ h \cdot (x^2+y^2+ax+by+c) + j \cdot ( x^2+y^2+a'x+b'y+c' ) = 0 $$

Questa equazione del fascio di circonferenze mi permette di ottenere tutte le circonferenze del fascio di rette al variare dei coefficienti h e j.

Nota. Se h=0 e j=1 ottengo l'equazione C₂. Viceversa, se h=1 e j=0 ottengo la circonferenza C₁.

Divido entrambi i lati dell'equazione per h

$$ \frac{1}{h} \cdot [ h \cdot (x^2+y^2+ax+by+c) + j \cdot x^2+y^2+a'x+b'y+c' ] = 0 \cdot \frac{1}{h} $$

$$ (x^2+y^2+ax+by+c) + \frac{j}{h} \cdot ( x^2+y^2+a'x+b'y+c' )  = 0  $$

Indico con k il rapporto j/h

$$ (x^2+y^2+ax+by+c) + k \cdot ( x^2+y^2+a'x+b'y+c' )  = 0  $$

In questo modo al variare di k posso ottenere tutte le circonferenze del fascio di rette, tranne la circonferenza C₂. 

Nota. Se k=0 ottengo l'equazione C₁. Viceversa, in questa forma del fascio di circonferenze non esiste alcun valore del parametro k in grado di generare la circonferenza C₂.

E così via.