Apotema
L'apotema di un poligono regolare è il segmento che congiunge il centro del poligono con il punto medio di uno dei suoi lati, ed è perpendicolare a quel lato.
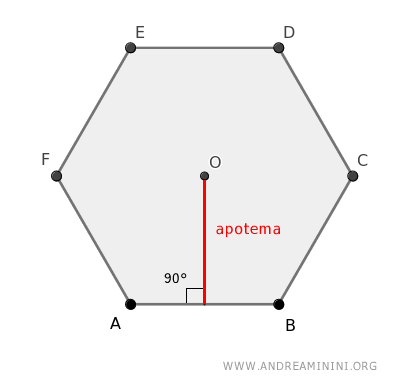
In altre parole, l'apotema rappresenta la distanza tra il centro del poligono e uno dei suoi lati.
Nei poligoni regolari l'apotema è anche il raggio della circonferenza inscritta nel poligono ossia l'inraggio.
La relazione tra l'apotema e il lato di un poligono regolare
Il rapporto tra l'apotema (a) e il lato (l) è un valore costante in un poligono ed è detto "numero fisso" (o costante f) del poligono. $$ f = \frac{a}{l} $$ Questo numero varia a seconda del numero dei lati del poligono.
Il numero fisso è costante indipendentemente dalle dimensioni del poligono e dalla lunghezza dei lati.
Ogni poligono è caratterizzato dal proprio numero fisso.
Ad esempio, in un pentagono il numero fisso è sempre il numero decimale illimitato e non periodico 0,688... Nei calcoli si utilizza il valore approssimato 0,688. In un esagono, invece, il numero fisso è sempre uguale al valore approssimato 0,866.
Ecco una tabella con le costanti f di alcuni poligoni
| Poligono | Costante f |
|---|---|
| Triangolo Equilatero | 0,289... |
| Quadrato | 0,5 |
| Pentagono | 0,688... |
| Esagono | 0,866... |
| Eptagono | 1,038... |
| Ottagono | 1,207... |
| Ennagono | 1,374... |
| Decagono | 1,539... |
| Dodecagono | 1,866... |
A cosa serve conoscere le costanti f?
L'uso delle costanti f permette di calcolare il lato conoscendo l'apotema $$ l = \frac{a}{f} $$ oppure di calcolare l'apotema conoscendo la misura del lato $$ a = l \cdot f $$
Ad esempio, un esagono ha ogni lato lungo 6 cm.
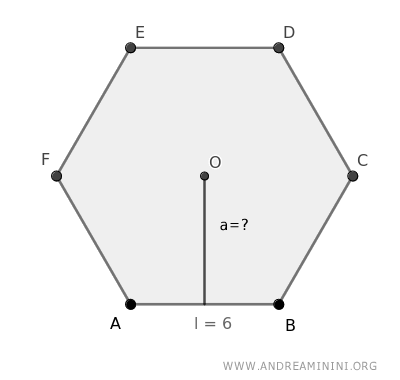
Posso calcolare l'apotema (a) sapendo che il numero fisso di ogni esagono regolare è circa f=0,866 $$ a = l \cdot f $$ $$ a = 6 \cdot 0,866 $$ $$ a = 5,196 $$
La costante f è molto utile nel calcolo dell'area di un poligono regolare.
$$ A = n \cdot \frac{l \cdot a}{2} $$
Sapendo che l'apotema è uguale al prodotto tra il lato (l) e la costante f, sostituisco a=l·f nella formula precedente
$$ A = n \cdot \frac{l \cdot l \cdot f}{2} $$
$$ A = n \cdot \frac{l^2 \cdot f}{2} $$
Il semiprodotto tra il numero dei lati del poligono per la costante f è indicato come costante φ (si legge"fi")
$$ \phi = \frac{n \cdot f}{2} $$
Si tratta di un'altra costante che dipende dalla costante f e cambia a seconda del numero dei lati del poligono
Quindi, posso anche riscrivere la formula dell'area del poligono regolare come il prodotto tra il quadrato del lato per la costante φ
$$ A = l^2 \cdot \phi $$
Ecco alcuni valori approssimati delle costanti φ
| Poligono | Costante φ |
|---|---|
| Triangolo Equilatero | 0,433... |
| Quadrato | 1 |
| Pentagono | 1,72... |
| Esagono | 2,598... |
| Eptagono | 3,634... |
| Ottagono | 4,828... |
| Ennagono | 6,182... |
| Decagono | 7,694... |
| Dodecagono | 11,196... |
Nota. Anche nel caso della costante φ sono molto utili le formule inverse. Ad esempio, posso calcolare la lunghezza del lato (l) conoscendo l'area (A) del poligono regolare $$ l = \sqrt{ \frac{A}{ \phi } } $$ Quest'ultima formula si ottiene ricavando il lato dalla formula dell'area $$ A = l^2 \cdot \phi $$ $$ l^2 = \frac{A}{ \phi } $$ $$ \sqrt{l^2} = \sqrt{ \frac{A}{ \phi } } $$ $$ l = \sqrt{ \frac{A}{ \phi } } $$
E così via.
