Ciclotomia (geometria)
La ciclotomia è un problema della geometria che consiste nel dividere una circonferenza in n parti congruenti utilizzando esclusivamente riga e compasso.
Il problema della ciclotomia risale all'antica Grecia ed è storicamente noto anche come il problema della costruzione dei poligoni regolari.
Se una circonferenza può essere divisa in n parti congruenti tramite riga e compasso, allora è anche possibile costruire un poligono regolare con n lati allo stesso modo. Ad esempio di un esagono.
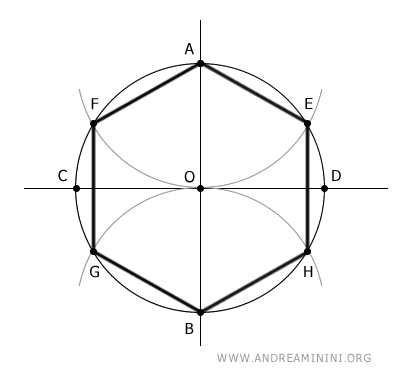
I filosofi e matematici greci cercarono di descrivere il mondo naturale attraverso forme geometriche pure. Tuttavia, gli antichi greci non riuscirono a risolvere il problema della ciclotomia in generale.
Ad esempio, i matematici greci dimostrarono di saper costruire poligoni regolari da 3 (triangolo) a 6 lati (esagono) ma già per poligoni regolari con 7 lati non si conosceva la soluzione. Nonostante gli sforzi di molti matematici nel corso dei secoli, la costruzione di un ettagono regolare restò un problema irrisolto per oltre duemila anni, fino a quando nel '800 Gauss non fornì la prova che questa costruzione non è possibile con i metodi classici.
Condizioni di Gauss per la ciclotomia
Il problema della ciclotomia venne risolto nel XIX secolo da Carl Friedrich Gauss.
Gauss determinò che una circonferenza può essere divisa in n parti congruenti con l'uso di riga e compasso se e solo se si verificano determinate condizioni:
- n è un numero primo nella forma
$$ n = 2^{2^k} + 1 $$
Dove k è un numero naturale (k∈N). Questi numeri sono anche noti come numeri di Fermat. - n non è un numero primo ma è il prodotto di una potenza di 2 e numeri primi distinti di Fermat
$$ n = 2^m \cdot p_1 \cdot p_2 \cdot ... \cdot p_3 $$
Dove m è un numero naturale (m∈N) mentre i numeri p1,...., pm sono uguali a 1 oppure sono dei numeri di Fermat $ 2^{2^k}+1 $ purché siano anche numeri primi e siano distinti tra loro.
In questo modo Gauss trovò la soluzione al problema della ciclotomia.
Queste condizioni o regole di Gauss escludono la possibilità di dividere una circonferenza in un numero di parti congruenti che sia un numero primo che non rientri nella forma di Fermat (come 7, 11, 13, ecc.) o un numero non primo che non soddisfa la seconda condizione sopra descritta. Pertanto, in questi casi non è possibile costruire un poligono regolare usando solo riga e compasso.
Esempio
Secondo la regola di Gauss è possibile determinare che è possibile suddividere una circonferenza in 3, 5, 17 parti congruenti (numeri primi di Fermat), così come in 4, 8, 16 parti (potenze di 2), o in numeri che sono il prodotto di questi come 15 (3 × 5), 10 (2 × 5), ecc.
Tuttavia, la regola di Gauss esclude la possibilità di costruire poligoni regolari con un numero di lati che sia, ad esempio, 7, 9, 11, 13, 14, ecc.
Verifica. Sapendo che i numeri di Fermat sono
| $ k $ | $ 2^{2^k} + 1 $ |
| 0 | 21+1=3 |
| 1 | 22+1=5 |
| 2 | 24+1=17 |
| 3 | 28+1=257 |
| 4 | 216+1=65537 |
Per la prima condizione della regola di Gauss seleziono tra i numeri di Fermat i numeri primi e deduco che una circonferenza è suddivisibile in 3, 5, 17, 257, 65537 parti
$$ n = \ 3 \ , \ 5 \ , \ 17 \ , \ 257 \ , \ ... $$
Va sottolineato che non tutti i numeri di Fermat sono numeri primi, solo i primi 5 lo sono. E' opportuno fare attenzione e considerare solo i numeri primi di Fermat.
Per la seconda condizione della regola di Gauss, devo considerare anche i numeri non primi (n) che posso ottenere moltiplicando le potenze di due 2m = 1, 2, 4, 8, ... dove è un intero non negativo (m≥0) per 1 o per dei numeri primi di Fermat (3, 5, 17, ...) distinti tra loro.
$$ 2^1 \cdot 3 = 6 \\ 2^1 \cdot 5 = 10 \\ 2^1 \cdot 17 = 34 \\ \vdots $$
$$ 2^2 = 4 \cdot 1 = 4 \\ 2^2 \cdot 3 = 12 \\ 2^2 \cdot 5 = 20 \\ 2^2 \cdot 17 = 68 \\ \vdots $$
$$ 2^3 = 8 \cdot 1 = 8 \\ 2^3 \cdot 3 = 24 \\ 2^3 \cdot 5 = 40 \\ \vdots $$
$$ 2^4 = 16 \cdot 1 = 16 \\ 2^4 \cdot 3 = 16 \cdot 3 = 48 \\ \vdots $$
Per la seconda condizione 2m·p1·p2···ps vanno aggiunti anche tutti i numeri non primi che sono il prodotto tra i numeri primi di Fermat distinti tra loro e una potenza di 2m con m≥0 ricordando che 20=1
$$ 2^0 \cdot 3 \cdot 5 = 15 \\ 2^0 \cdot 3 \cdot 17 = 51 \\ \vdots $$
In conclusione, mettendo insieme tutti i numeri appena trovati, posso suddividere con riga e compasso una circonferenza nelle seguenti n parti congruenti:
$$ n = \ 3 \ , \ 4 \ , \ 5 \ , \ 6 \ , \ 8 \ , \ 10 \ , \ 12 \ , \ 15 \ , \ 16 \ , \ 17 \ , ... $$
Quindi, posso disegnare con riga e compasso altrettanti poligoni regolari con n=3, 4, 5, 6, 8, 10, 12, 15, 16, 17 lati.
Non posso, invece, suddividere la circonferenza con riga e compasso in 7, 9, 11, 13, 14, ... parti congruenti. Pertanto, non posso nemmeno disegnare poligoni regolari con sette, nove, ecc. lati usando solo riga e compasso.
Osservazioni
Alcune osservazioni e note a margine
- Il risultato ottenuto da Gauss non ha soltanto risolto un antico problema geometrico ma ha anche aperto la strada a nuove aree di indagine nella teoria dei numeri, nell'algebra e nella matematica discreta. La ciclotomia è strettamente legata alla teoria dei campi ciclotomici e alle equazioni polinomiali, e ha importanti applicazioni in crittografia e teoria dell'informazione. Quindi, oggi la ciclotomia rappresenta anche un ponte tra la geometria classica e la teoria moderna dei numeri, dimostrando come problemi storici possano portare a profonde intuizioni matematiche che travalicano secoli di pensiero.
In altre parole, la semplice domanda su come dividere una circonferenza ha portato a una comprensione più profonda della simmetria, della fattorizzazione dei numeri e della struttura algebrica dei polinomi, ponendo le basi per sviluppi futuri in molteplici rami della matematica.
E così via.
