Il raggio di un cerchio inscritto in un triangolo
Il raggio di un cerchio inscritto in un triangolo è uguale al rapporto tra l'area (A) e il semiperimetro (p) del triangolo. $$ r = \frac{A}{p} $$
Questa formula mostra un'interessante relazione tra l'area e le dimensioni perimetrali del triangolo e il raggio della circonferenza inscritta (incerchio).
Mi permette di risolvere problemi che coinvolgono le proprietà dei triangoli e dei cerchi.
Un esempio pratico
Prendo come esempio un triangolo ABC.
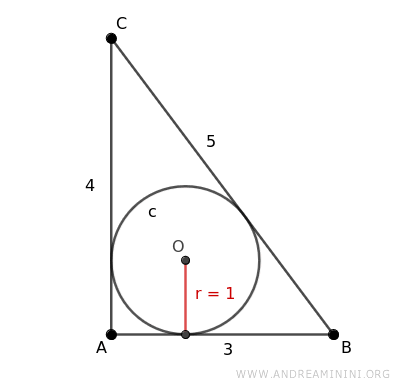
I lati del triangolo hanno queste misure AB=3, AC=4, BC=5 mentre il raggio della circonferenza inscritta è r=1.
Quindi, il semiperimetro del triangolo ABC è uguale a p=6.
$$ 2p = 3+4+5 $$
$$ 2p = 12 $$
$$ p = 6 $$
L'area del triangolo A=6 la ottengo tramite il semiprodotto della base AB=3 per l'altezza AC=4.
$$ Area_{ABC} = \frac{ \overline{AB} \cdot \overline{AC} }{2} $$
$$ Area_{ABC} = \frac{ 3 \cdot 4 }{2} = \frac{12}{2} = 6 $$
A questo punto calcolo il rapporto tra l'area A=6 e il semiperimetro p=6 del triangolo.
$$ r= \frac{Area_{ABC}}{p} = \frac{6}{6}=1 $$
Il risultato è la lunghezza del raggio della circonferenza inscritta.
Nota. In questo caso, per semplificare i calcoli ho considerato nell'esempio un triangolo rettangolo ma lo stesso avviene in qualsiasi altro tipo triangolo.
La dimostrazione
Considero un triangolo qualsiasi ABC.
Traccio le bisettrici degli angoli del triangolo per trovare l'incentro, ossia il centro della circonferenza inscritta (incerchio) nel triangolo.
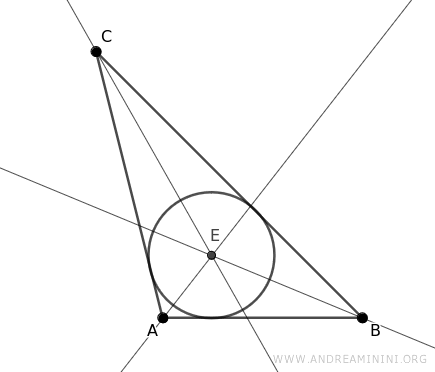
La circonferenza inscritta è tangente ai tre lati del triangolo nei punti D, F, G.
Quindi, i segmenti EF, EG, EH sono i raggi della circonferenza e, ovviamente, sono congruenti EF≅EG≅EH.
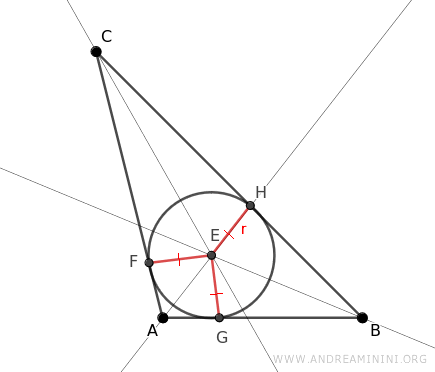
Inoltre, tutti i raggi sono perpendicolari ai lati del triangolo perché passano nei punti di tangenza della circonferenza.
Quindi, sono anche le altezze dei triangoli ACE, ABE, BCE.
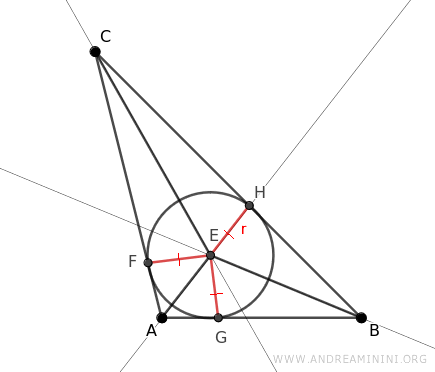
I triangoli ACE, ABE, BCE coprono interamente la superficie del triangolo ABC.
Quindi, la somma delle aree dei triangoli ACE, ABE, BCE è uguale all'area del triangolo ABC.
$$ \text{Area}_{ABC} = \text{Area}_{ACE} + \text{Area}_{ABE} + \text{Area}_{BCE} $$
L'area di un triangolo si ottiene tramite il semiprodotto della base per l'altezza.
Nel caso dei triangolo ACE, ABE, BCE la base è un lato del triangolo ABC e l'altezza è il raggio r della circonferenza inscritta.
$$ \text{Area}_{ABC} = \frac{ \overline{AC} \cdot r }{2} + \frac{ \overline{AB} \cdot r }{2} + \frac{ \overline{BC} \cdot r }{2} $$
Metto in evidenza il raggio r.
$$ \text{Area}_{ABC} = r \cdot ( \frac{ \overline{AC} }{2} + \frac{ \overline{AB} }{2} + \frac{ \overline{BC} }{2} ) $$
$$ \text{Area}_{ABC} = r \cdot ( \frac{ \overline{AC} + \overline{AB} + \overline{BC} }{2} ) $$
La somma dei segmenti AC+AB+BC=P è il perimetro (P) del triangolo ABC, ovvero il doppio del suo semiperimetro P=2p
$$ \text{Area}_{ABC} = r \cdot ( \frac{ 2p }{2} ) $$
$$ \require{cancel} \text{Area}_{ABC} = r \cdot ( \frac{ \cancel{2} p }{ \cancel{2} } ) $$
$$ \text{Area}_{ABC} = r \cdot p $$
Questo dimostra che l'area del triangolo ABC è uguale al prodotto del raggio (r) della circonferenza inscritta e del semiperimetro (p) del triangolo.
E così via.
