Teorema degli angoli inscritti

In una circonferenza l'ampiezza di un angolo inscritto è sempre uguale alla metà dell'ampiezza dell'arco sotteso da quell'angolo.

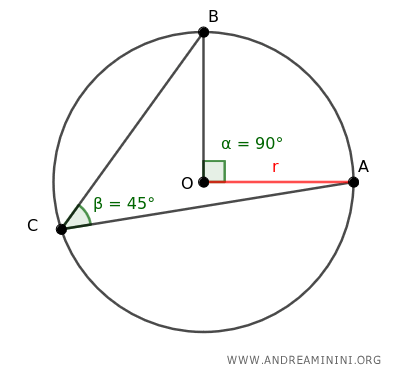
In altre parole, se ho un angolo inscritto che sottende un arco di α gradi, allora l'angolo inscritto avrà un'ampiezza di α/2​ gradi.

Questo teorema è valido per qualsiasi arco e angolo inscritto in una circonferenza, non solo per le semicirconferenze.

Un esempio pratico

Considero una circonferenza con centro O e raggio r.

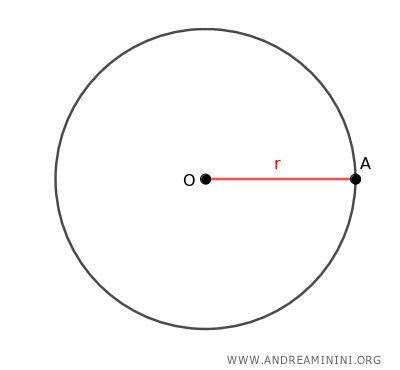
Prendo tre punti distinti qualsiasi A, B e C della circonferenza.

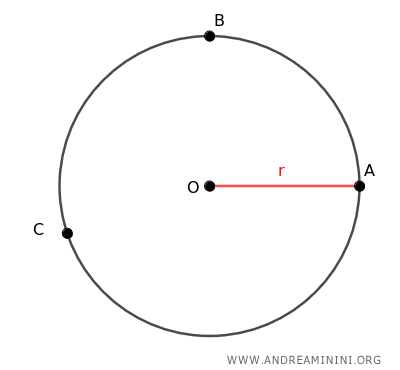
Traccio i segmenti BC e AC e l'angolo inscritto ∠ACB alla circonferenza.

In questo caso l'angolo ACB è uguale a 45°.

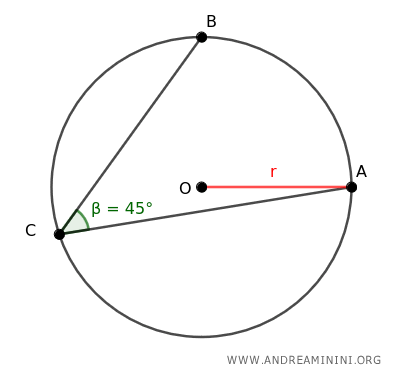
Secondo il teorema degli angoli inscritto, un angolo inscritto ha un'ampiezza pari alla metà dell'ampiezza dell'arco sotteso dallo stesso arco.

In questo caso l'arco è il tratto AB della circonferenza.

Traccio i segmenti OA e OB per calcolare l'angolo al centro ∠AOB che sottende l'arco AB.

 

L'angolo ∠AOB che sottende l'arco AB ha un'ampiezza di 90° pari al doppio dell'angolo inscritto (45°).

 

La dimostrazione

 

Considero una circonferenza con centro O e tre punti A, B, C sulla circonferenza.

I punti A e B sulla circonferenza formano l'angolo inscritto ∠ACB

 

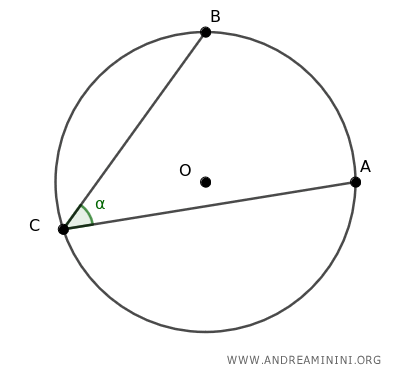
Poi traccio i segmenti OA e OB.

 

L'angolo al centro ∠AOB sottende l'arco AB.

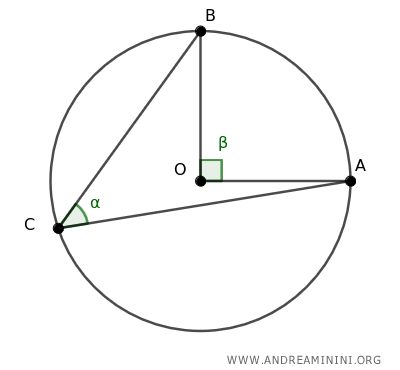
Traccio anche il segmento OC.

I triangoli OAC e OBC sono entrambi triangoli isosceli poiché OA e OC sono raggi della stessa circonferenza, e lo stesso vale per OB e OC.

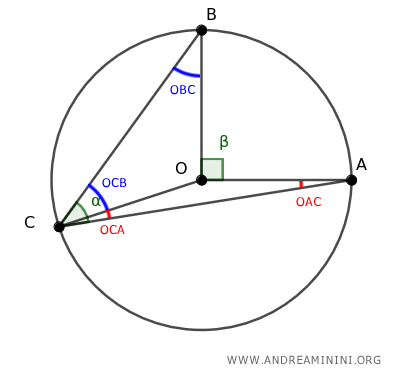
Sapendo che gli angoli alla base dei triangoli isosceli sono congruenti, deduco che ∠OCA≡∠OAC e ∠OCB≡∠OBC.

L'angolo inscritto ∠ACB è la somma degli angoli ∠OCA e ∠OCB.

$$ ∠ACB = ∠OCA + ∠OCB $$

Ora prolungo il segmento OC fino al punto D ottenendo il diametro CD della circonferenza.

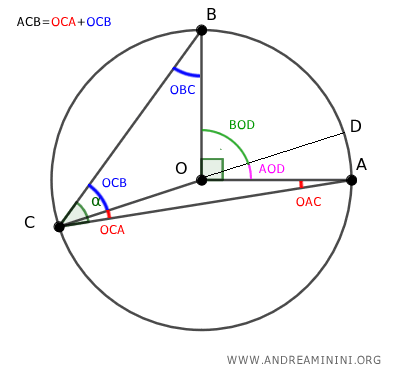
L'angolo ∠AOD è un angolo esterno del triangolo OAC, quindi per il teorema dell'angolo esterno è congruente con la somma degli angoli interni non adiacenti ∠OCA+∠OAC del triangolo OAC

$$ ∠AOD = ∠OCA + ∠OAC $$

Poiché ∠OCA≅∠OAC sono due angoli congruenti posso anche scrivere ∠AOD = 2 ∠OCA

$$ ∠AOD = 2 ∠OCA $$

Allo stesso modo l'angolo ∠BOD è un angolo esterno del triangolo OBC e, sempre per il teorema dell'angolo esterno, è congruente con la somma degli angoli interni non adiacenti ∠OBC+∠OCB del triangolo OAC

$$ ∠BOD = ∠OBC + ∠OCB $$

Poiché ∠OBC≅∠OCB sono congruenti, posso anche scrivere ∠BOD = 2 ∠OCB

$$ ∠BOD = 2 ∠OCB $$

Sapendo che l'angolo ∠AOB può essere espresso come la somma degli angoli ∠AOD+∠BOD.

$$ ∠AOB = ∠AOD + ∠BOD $$

Poiché ∠AOD = 2 ∠OCA e ∠BOD = 2 ∠OCB

 

$$ ∠AOB = 2 ∠OCA + 2 ∠OCB $$

$$ ∠AOB = 2 \cdot ( ∠OCA + ∠OCB ) $$

Sapendo che ∠OCA + ∠OCB = ∠ACB

$$ ∠AOB = 2 \cdot ∠ACB $$

 

Questo dimostra che l'angolo inscritto∠ACB è esattamente la metà dell'ampiezza dell'arco sotteso ∠AOB.

$$ \frac{ ∠AOB }{2 } = ∠ACB $$

E così via.