Teorema dell'equivalenza dell'area tra cerchio e triangolo

L'area di un cerchio è uguale all'area di un triangolo che ha per base la lunghezza della circonferenza e per altezza il raggio del cerchio. $$ \pi \cdot r^2 = \frac{1}{2} \cdot c \cdot r $$

In altre parole, il cerchio è equivalente al triangolo che ha per base la circonferenza (c) e per altezza il raggio (r).

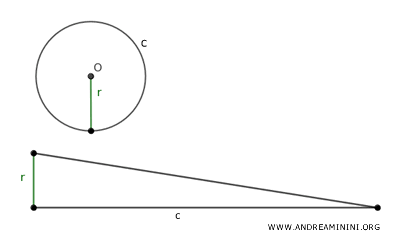
L'area A di un cerchio si calcola facendo il prodotto tra pi greco (p=3.14...) e il quadrato del raggio (r).

$$ A = \pi r^2 $$

La lunghezza della circonferenza \( c \) del cerchio è, invece, data dal doppio prodotto tra pi greco e il raggio (r).

$$ c = 2\pi r $$

Se considero un triangolo con base equivalente alla circonferenza del cerchio (\(c = 2\pi r\)) e altezza equivalente al raggio del cerchio (\(h = r\)), l'area \(A_t\) di tale triangolo è data da:

$$ A_t = \frac{1}{2} \cdot base \cdot altezza = \frac{1}{2} \cdot C \cdot r = \frac{1}{2} \cdot 2\pi r \cdot r = \pi r^2 $$

Quindi, l'area del cerchio e l'area di questo specifico triangolo sono uguali.

Nota. Questo teorema non è uno tra i più comunemente citati nei testi di geometria tradizionali, ma è una proprietà interessante che collega l'area di un cerchio con quella di un triangolo. E' utile da tenere a mente.  Non è tradizionalmente conosciuto con un nome specifico, ma è più un'osservazione geometrica derivante dalle formule per l'area del cerchio e del triangolo. Quindi, si tratta di una conseguenza diretta delle definizioni di area del cerchio e del triangolo, piuttosto che un teorema specifico.

La dimostrazione

Considero un cerchio con una circonferenza c e un raggio r.

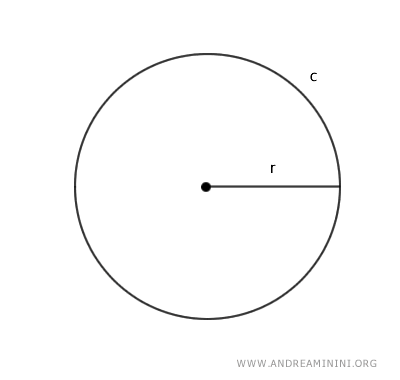
Poi costruisco un poligono regolare inscritto nella circonferenza. Ad esempio un esagono.

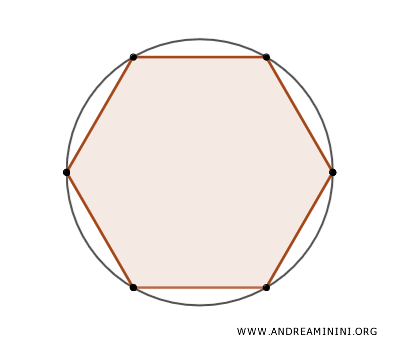
Posso dedurre che l'area del poligono regolare inscritto $ A_p $ è inferiore alla superficie del cerchio $ A_c $.

$$ A_p < A_c  $$

A questo punto costruisco un poligono regolare circoscritto alla circonferenza con lo stesso numero di lati del precedente.

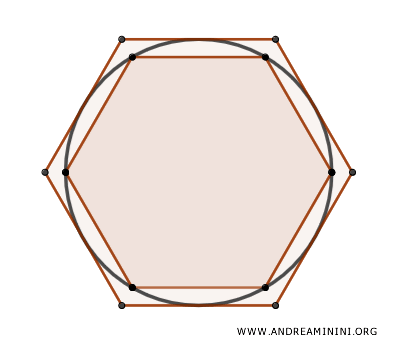
In questo caso deduco che l'area del poligono circoscritto $ A_{p'} $ è maggiore rispetto all'area del cerchio $ A_c $.

$$ A_p < A_c < A_{pì'}  $$

Quindi, l'area del cerchio $ A_c $ è l'elemento che delimita la classe delle aree dei poligoni regolari inscritti dalla classe delle aree dei poligono regolari circoscritti.

Aumentando il numero dei lati ai poligono inscritti e circoscritti, l'area dei poligono $ A_p $ tende ad avvicinarsi sempre più a quella del cerchio $ A_c $.

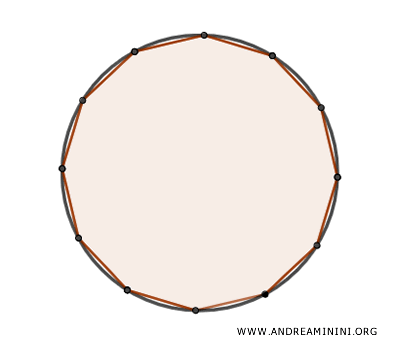
Pertanto, portando al limite questo ragionamento, posso ipotizzare che esista un poligono regolare con infiniti lati che abbia la stessa area del cerchio.

$$ A_c = A_p $$

Secondo il teorema dei poligoni circoscrivibili a una circonferenza, qualsiasi poligono regolare è sempre equivalente a un triangolo che ha la base congruente al perimetro del poligono e l'altezza congruente con l'apotema del poligono.

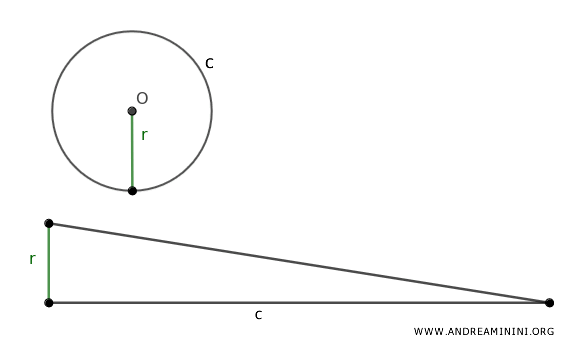
Nota. Nel caso di un poligono regolare con infiniti lati, l'apotema del poligono coincide con il raggio della circonferenza circoscritta. Pertanto, l'altezza del triangolo equivalente al poligono regolare è congruente con il raggio della circonferenza.

Quindi, l'area del poligono regolare con infiniti lati è uguale all'area del triangolo equivalente:

$$ A_c = A_p = A_t = \frac{1}{2} \cdot p \cdot a $$

Dove $ p $ è il perimetro del poligono mentre $ a $ è l'apotema del poligono.

Sapendo che il perimetro del poligono regolare coincide con la circonferenza $ p = c $ e che l'apotema coincide con il raggio della circonferenza $ a = r $

$$ A_c = A_p = A_t = \frac{1}{2} \cdot c \cdot r $$

In conclusione, l'area della circonferenza $ A_c $ è uguale all'area del triangolo che ha per base la circonferenza e per altezza il raggio.

$$ A_c = \frac{1}{2} \cdot c \cdot r $$

Verifica. Per fare una rapida verifica basta ricordarsi che l'area del cerchio è $ A_c = \pi r^2 $  $$ A_c = \frac{1}{2} \cdot c \cdot r $$ $$ \pi r^2 = \frac{1}{2} \cdot c \cdot r $$ La lunghezza della circonferenza è, invece, $ c = 2 \pi r $  $$ \pi r^2 = \frac{1}{2} \cdot ( 2 \pi r ) \cdot r $$ Semplifico e svolgo i calcoli al secondo membro dell'equazione  $$ \require{cancel} \pi r^2 =  \frac{1}{ \cancel{2}} \cdot \cancel{2} \pi r^2 $$ $$ \pi r^2 =  \pi r^2 $$ L'identità è soddisfatta.

E così via.