Teorema degli angoli al centro e alla circonferenza corrispondenti

In una circonferenza gli angoli alla circonferenza α hanno un'ampiezza pari alla metà dell'angolo al centro β corrispondente che insiste sullo stesso arco AB. $$ \alpha = \frac{1}{2} \beta $$ Esempio: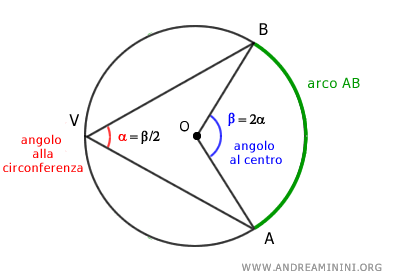

In alternativa e in modo del tutto equivalente, posso affermare che gli angoli al centro β hanno un'ampiezza doppia rispetto agli angoli alla circonferenza corrispondenti α

$$ \beta = 2 \alpha $$

Poiché esiste un solo angolo al centro e infiniti angoli alla circonferenza che insistono su un arco AB, da questo deduco che tutti gli angoli alla circonferenza α che insistono sullo stesso arco AB sono congruenti tra loro.

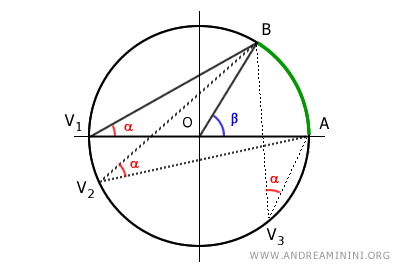
Inoltre, se un angolo alla circonferenza insiste su una semicirconferenza allora è un angolo retto (90°) perché in questo caso l'angolo al centro è un angolo piatto (180°).

La dimostrazione

Per dimostrare questo teorema devo considerare tre casi, a seconda se il centro della circonferenza O si trova su un lato, all'interno o all'esterno dell'angolo alla circonferenza.

A] Il centro si trova su un lato dell'angolo alla circonferenza

Se il centro O della circonferenza si trova su un lato dell'angolo alla circonferenza α, allora questo lato (AV) è un diametro della circonferenza.

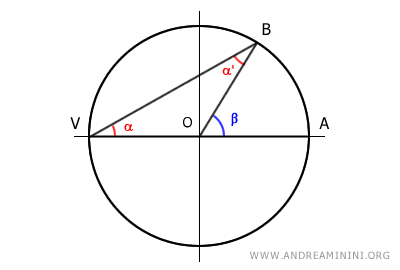
Poiché AV è un diametro della circonferenza, la sua metà OV è un raggio della circonferenza.

In questo caso il triangolo VBO è un triangolo isoscele, perché ha per lati obliqui due raggi della circonferenza OV≅OB.

Sapendo che ogni triangolo isoscele ha gli angoli adiacenti alla base congruenti, deduco che gli angoli α≅α' sono congruenti.

$$ \alpha = \alpha' $$

In base al teorema dell'angolo esterno di un triangolo, l'angolo al centro β è un angolo esterno del triangolo VBO ed è uguale alla somma degli angoli interni non adiacenti α+α'

$$ \beta = \alpha + \alpha' $$

Poiché α≅α' sono congruenti posso scrivere α+α'=2α

Pertanto, l'angolo al centro (β) è il doppio dell'angolo alla circonfrenza (2α)

$$ \beta = 2 \alpha $$

Di conseguenza, l'angolo alla circonferenza (α) è la metà dell'angolo al centro (β/2).

$$ \alpha = \frac{1}{2} \beta $$

B] Il centro si trova dentro l'angolo alla circonferenza

In questo caso il centro O della circonferenza si trova all'interno dell'angolo alla circonferenza α.

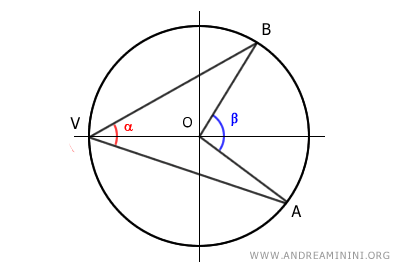
Traccio il diametro VC per dividere in due parti l'angolo alla circonferenza α e l'angolo al centro β.

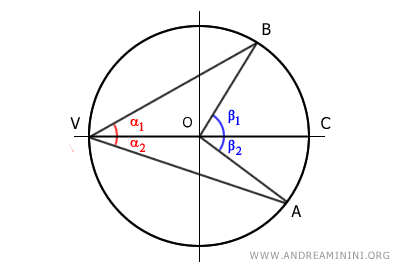
Pertanto, ora l'angolo alla circonferenza e al centro sono i seguenti:

$$ \alpha = \alpha_1 + \alpha_2 $$

$$ \beta = \beta_1 + \beta_2 $$

In questo modo entrambi gli angoli alla circonferenza α₁ e α₂ hanno un lato che coincide con il diametro della circonferenza.

Nel punto [A] di questa dimostrazione ho già dimostrato che gli angoli alla circonferenza che hanno un lato coincidente con il diametro hanno un'ampiezza uguale alla metà degli angoli al centro corrispondenti.

Quindi, gli angoli al centro α₁ e α₂ hanno un'ampiezza pari alla metà dei rispettivi angoli al centro corrispondenti β₁ e β₂

$$ \alpha_1 = \frac{1}{2} \beta_1 $$

$$ \alpha_2 = \frac{1}{2} \beta_2 $$

Sapendo che l'angolo alla circonferenza è la somma degli angoli α=α₁+α₂

$$ \alpha = \alpha_1 + \alpha_2 $$

Sostituisco α₁=(1/2)β₁ e α₂=(1/2)β₂

$$ \alpha = \frac{1}{2} \beta_1 + \frac{1}{2} \beta_2 $$

$$ \alpha = \frac{1}{2} \cdot ( \beta_1 + \beta_2 ) $$

Infine, poichè l'angolo al centro è la somma degli angoli β =β₁+β₂

$$ \alpha = \frac{1}{2} \cdot \beta $$

Questo dimostra che l'angolo alla circonferenza (α) è la metà dell'angolo al centro (β/2).

Di conseguenza, l'angolo al centro (β) è il doppio dell'angolo alla circonferenza (2α).

$$ \beta = 2 \alpha $$

C] Il centro si trova all'esterno dell'angolo alla circonferenza

Resta da studiare l'ultimo caso possibile, quello in cui il centro O della circonferenza si trova all'esterno dell'angolo alla circonferenza α.

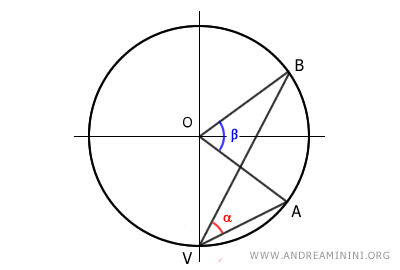
Traccio il diametro VC in modo da ottenere altri due angoli che per costruzione sono legati agli angoli α e β

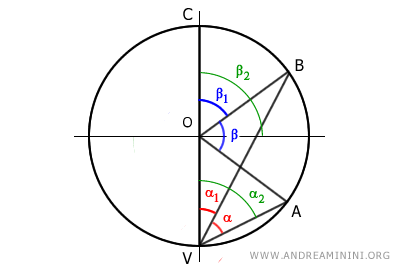
Per costruzione l'angolo alla circonferenza è α=α₂-α₁ mentre l'angolo al centro è β=β₂-β₁

$$ \alpha = \alpha_2 - \alpha_1 $$

$$ \beta = \beta_2 - \beta_1 $$

L'angolo α₁ è un angolo alla circonferenza che ha per lato un diametro (VC) della circonferenza, quindi come già dimostrato nel punto [A] di questa dimostrazione, la sua ampiezza è pari alla metà dell'angolo al centro corrispondente β₁

$$ \alpha_1 = \frac{1}{2} \beta_1 $$

Anche l'angolo α₂ è un angolo alla circonferenza che ha per lato un diametro (VC) della circonferenza e, per lo stesso motivo, la sua ampiezza è pari alla metà dell'angolo al centro corrispondente β₂

$$ \alpha_2 = \frac{1}{2} \beta_2 $$

Una volta noti α₁=β₁/2 e α₂=β₂/2 li sostituisco nell'equazione α= α₂-α₁

$$ \alpha = \alpha_2 - \alpha_1 $$

$$ \alpha = \frac{1}{2} \beta_2 - \frac{1}{2} \beta_1 $$

$$ \alpha = \frac{1}{2} \cdot ( \beta_2 - \beta_1 ) $$

Sapendo che l'angolo al centro è pari alla differenza β=β₂-β₁

$$ \alpha = \frac{1}{2} \cdot \beta $$

Questo dimostra che l'angolo alla circonferenza (α) è la metà dell'angolo al centro (β/2).

Di conseguenza, l'angolo al centro (β) è il doppio dell'angolo alla circonferenza (2α)

$$ \beta = 2 \alpha $$

In conclusione, il teorema è dimostrato in tutti i casi possibili

E così via.