Le simmetrie nei grafici delle funzioni
La simmetria di un grafico è una trasformazione geometrica che lascia invariata o parzialmente invariata la forma della funzione.
Esistono diverse simmetrie fondamentali rispetto agli assi cartesiani o al punto origine.
Inoltre, i grafici possono essere modificati anche introducendo i valori assoluti.
Simmetria rispetto all’asse x
Una funzione è simmetrica rispetto all’asse x se vale:
\[ y = -f(x) \]
Ogni punto del grafico di f(x) viene riflesso rispetto all’asse x.
In pratica, se un punto appartiene al grafico di f(x), allora il punto con ordinata opposta appartiene a quello di -f(x).
Esempio
Considero la funzione
$$ f(x) = \sqrt{x} $$
La simmetria della funzione rispetto all’asse ( x ) si ottiene cambiando il segno ai valori della funzione:
\[ g(x) = -f(x) \]
Sostituendo l’espressione di ( f(x) ), risulta
$$ g(x) = -f(x) = -\sqrt{x} $$
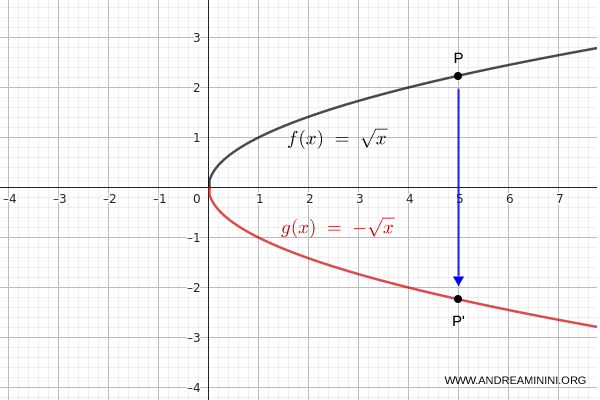
Il dominio resta invariato, cioè \( x \ge 0 \), mentre il grafico di \( g(x) \) è il riflesso del grafico di \( y = \sqrt{x} \) rispetto all’asse \( x \).
Simmetria rispetto all’asse y
Una funzione è simmetrica rispetto all’asse y se vale:
$$ y = f(-x) $$
Il grafico viene riflesso sull’asse y. Ogni punto del grafico con ascissa x viene affiancato da un punto con ascissa opposta -x.
Esempio
Considero la funzione
$$ f(x) = x^3 $$
La simmetria della funzione rispetto all’asse \( y \) si ottiene sostituendo \( x \) con \( -x \):
\[ g(x) = f(-x) \]
Calcolando esplicitamente, risulta
$$ g(x) = f(-x) = (-x)^3 = -x^3 $$
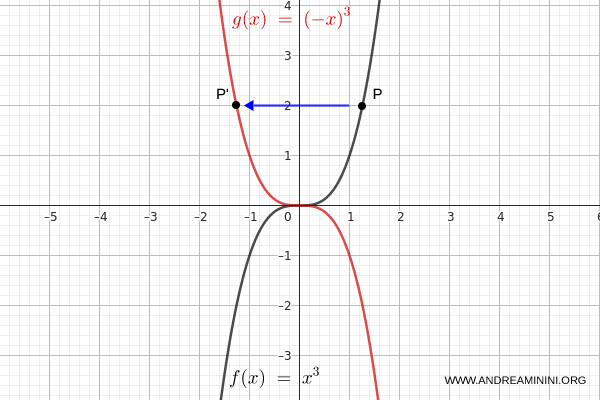
Quindi il grafico di \( g(x) \) è il simmetrico rispetto all’asse \( y \) del grafico di \( y = x^3 \).
Simmetria centrale rispetto all’origine
Una funzione è simmetrica rispetto all’origine (O) se vale:
$$ y = -f(-x) $$
Il grafico viene riflesso prima sull’asse y, poi sull’asse x. È detta simmetria centrale perché ogni punto \( (x, f(x)) \) ha un corrispondente opposto \( (-x, -f(x)) \).
Esempio
Considero la funzione
$$ f(x) = x^2 $$
La simmetria centrale della funzione rispetto all’origine \( O \) si ottiene applicando la trasformazione
\[ g(x) = -f(-x) \]
Sostituendo l’espressione di \( f(x) \), ottengo
$$ g(x) = -f(-x) = -(-x)^2 = -x^2 $$
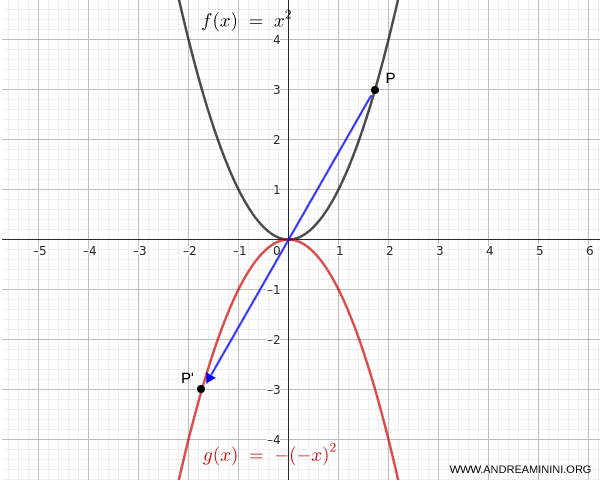
Quindi il grafico di \( g(x) \) è il simmetrico centrale rispetto all’origine del grafico di \( y = x^2 \).
Il grafico del valore assoluto della funzione
La funzione \( y = |f(x)| \) ha un comportamento spezzato:
- dove \( f(x) \ge 0 \), il grafico resta invariato.
- dove \( f(x) < 0 \), la parte negativa viene riflessa sull’asse x.
Esempio
Se \( f(x) = x \), allora il valore assoluto della funzione è
\[ |f(x)| = |x| \]
Per eliminare il valore assoluto, distinguo i due casi:
\[
|f(x)| = |x| =
\begin{cases}
x & \text{se } x \ge 0 \\ \\
-x & \text{se } x < 0
\end{cases}
\]
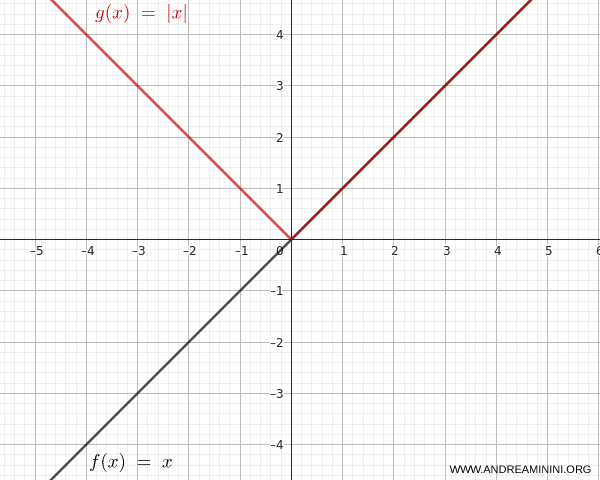
Il grafico coincide con la retta \( y = x \) per \( x \ge 0 \) e con la retta \( y = -x \) per \( x < 0 \).
Nel complesso si ottiene una curva a forma di “V”, simmetrica rispetto all’asse y.
Il grafico della funzione con valore assoluto dell’argomento
La funzione \( y = f(|x|) \) è costruita a partire dal grafico di f(x) per \( x \ge 0 \). Poi, tale parte viene riflessa sull’asse y.
- Per \( x > 0 \), il grafico è uguale a f(x).
- Per \( x < 0 \), si prende il grafico di f(x) con \( x > 0 \), e si esegue una simmetria rispetto all’asse y.
Esempio
Considero la funzione:
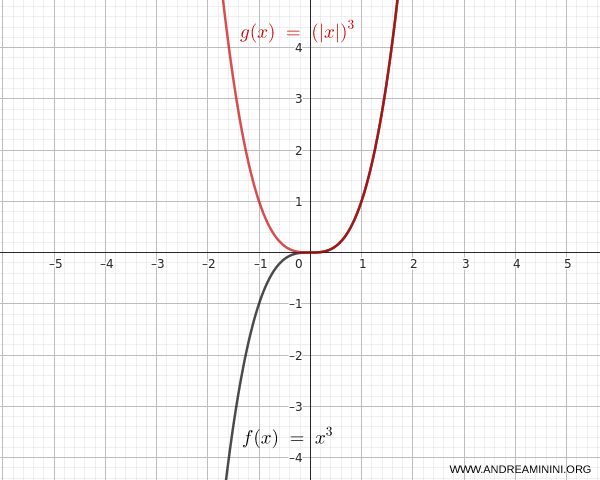
$$ f(x) = ( |x| )^3 $$
Per eliminare il valore assoluto, distinguo i due casi.
\[
f(|x|) =
\begin{cases}
x^3 & \text{se } x \ge 0 \\ \\
(-x)^3 = -x^3 & \text{se } x < 0
\end{cases}
\]
Quindi, per \( x \ge 0 \) il grafico coincide con quello di \( y = x^3 \), mentre per \( x < 0 \) ottengo il suo simmetrico rispetto all’asse \( y \).
E così via.
