Le funzioni polinomiali

Cos'è una funzione polinomiale

Una funzione è detta polinomiale quando l'espressione della funzione è un polinomio $$ y = P(x) $$

Ecco un esempio di funzione polinomiale

$$ f(x) = x^3 - x^2 - 2x + 2 $$

In questo caso l'espressione della funzione è un polinomio P(x)=x³-x² - 2x +2 di terzo grado con una variabile incognita.

Sostituendo i valori della variabile indipendente x con alcuni punti del dominio, in questo caso il dominio è l'insieme dei numeri reali, posso calcolare il corrispondente valore della funzione y=f(x)

Ad esempio, calcolo il valore della funzione intorno al punto x= 0.

$$ \begin{array}{c|lcr} x & \text{y} \\ \hline -3 & -28 \\ -2 & -6 \\ -1 & 2 \\ 0 & 2 \\ 1 & 0 \\ 2 & 2 \\ 3 & 14 \end{array} $$

Ogni riga della tabella precedente indica le coordinate (x;y) della funzione sul piano cartesiano.

Questo mi permette di costruire una stima del grafico della funzione intorno a un punto.

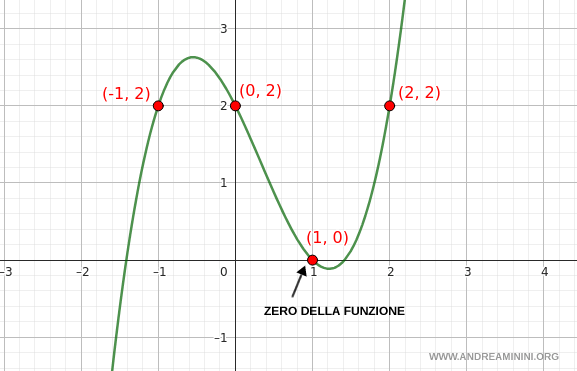
I punti in cui la funzione polinomiale si annulla y(x)=0 sono detti zeri del polinomio o della funzione polinomiale.

Negli zeri del polinomio il grafico della funzione polinomiale interseca l'asse delle ascisse (x) perché il valore della funzione è y=0.

In questo esempio c'è un unico zero della funzione alle coordinate (x;y)=(1;0) quando la variabile indipendente è x=1.

Nota. Una funzione può avere uno o più zeri oppure non averne affatto. I punti in cui la funzione polinomiale tende a più o meno infinito, invece, sono detti poli.

E così via.