Le funzioni concave e convesse

Funzione convessa

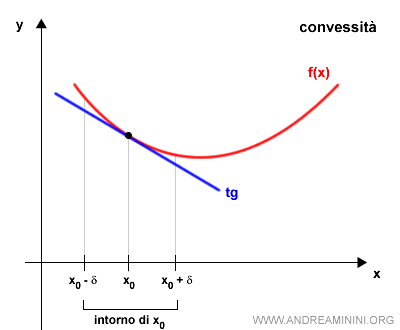
Una funzione f(x) è convessa se in un intervallo [a,b] se per ogni punto x₀∈[a,b] il grafico della funzione in [a,b] è al di sopra della retta tangente al grafico nel punto (x₀,f(x₀).

Funzione concava

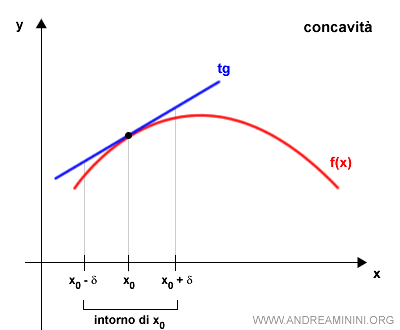
Una funzione f(x) è concava se in un intervallo [a,b] se per ogni punto x₀∈[a,b] il grafico della funzione in [a,b] è al di sotto della retta tangente al grafico nel punto (x₀,f(x₀).

Nei prossimi paragrafi spiego come riconoscere una funzione concava o convessa tramite l'osservazione del grafico o con la derivata della funzione.

Come capire se una funzione è concava o convessa

Ho una funzione definita in un intervallo [a,b] e un punto x₀ di [a,b], nell'intervallo [a,b] la funzione è

• convessa, se il grafico della funzione in [a,b] è al di sopra della retta tangente al grafico nel punto (x₀,f(x₀))
  
• concava, se il grafico della funzione in [a,b] è al di sotto della retta tangente al grafico nel punto (x₀,f(x₀))
  

Una funzione può essere concava o convessa in tutti l'intervallo in cui è definita o solo nell'intorno di alcuni punti.

Pertanto, una stessa funzione potrebbe anche essere concava in alcuni punti e convessa in altri.

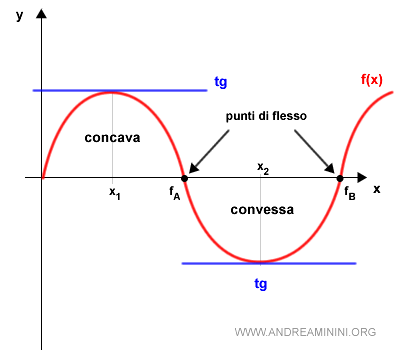
Il passaggio dalla concavità alla convessità (e viceversa) avviene in punti detti punti di flesso.

Cosa sono i punti di flesso

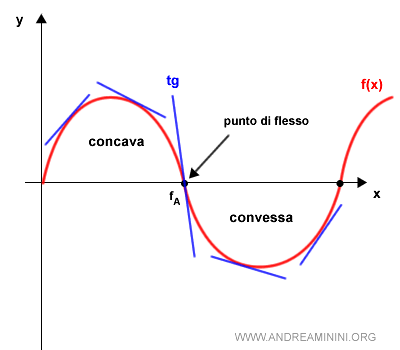
Se la retta tangente è al di sotto del grafico della funzione a sinistra di x₀ e al di sopra a destra di x₀, nel punto x₀ c'è un flesso, in questo caso la funzione passa dalla convessità alla concavità.

Ad esempio, in questo grafico il punto f_A è un punto di flesso in cui la funzione passa dalla concavità alla convessità.

Prima del punto f_A il grafico della funzione (rosso) è sempre al di sotto della retta tangente (blu). Dopo il punto fA è sempre al di sotto.

Può ovviamente accadere anche l'inverso.

Se la retta tangente è al di sotto del grafico della funzione a sinistra di un punto x₀ e al di sopra a destra di x₀ , nel punto x₀ la funzione ha un flesso, ossia un passaggio dalla convessità alla concavità.

Ad esempio, nel punto f_B c'è un altro punto di flesso in cui la funzione passa dalla convessità alla concavità.

In questo caso, il grafico della funzione (rosso) è sempre al di sotto della retta tangente (blu) prima del punto f_A e sempre al di sopra dopo il punto f_A.

Criterio di concavità e convessità

Posso capire se una funzione è convessa o concava anche senza guardare il grafico, studiando la derivata della funzione.

Criterio di convessità

Se la derivata prima f'(x) è crescente nell'intervallo [a,b], funzione f(x) è convessa. Pertanto, la funzione è convessa se la derivata seconda f"'(x)≥0. $$ f"(x)≥0 \:\:\:\: \forall x \in (a,b) $$

Dire che la derivata prima f'(x) è crescente e la derivata seconda f"(x)>=0 è maggiore di zero, è la stessa cosa.

$$ f"(x) \ge 0 $$

Se applico il criterio di monotonia alla derivata prima, la derivata seconda è sempre maggiore o uguale a zero se la derivata prima è crescente.

$$ f"(x) \ge 0 \Leftrightarrow f'(x) \:\: \text{ è crescente} $$

Esempio

La funzione f(x)=x² è convessa nel punto x=0 perché la derivata prima f'(x)=2x è crescente nell'intorno di x=0.

Se la f'(x) è crescente allora la derivata seconda f"(x)≥0 nell'intorno di x=0.

E' effettivamente convessa in x=0 perché un'eventuale retta tangente della funzione si troverebbe al di sotto del grafico della funzione.

Criterio di concavità

Se la derivata prima f'(x) è decrescente nell'intervallo [a,b], funzione f(x) è concava. Pertanto, la funzione è concava se la derivata seconda f"(x)<=0. $$ f"(x)≤0 \:\:\:\: \forall x \in (a,b) $$

Dire che la derivata prima f'(x) è decrescente e la derivata seconda f"(x)≤0 è minore di zero, è la stessa cosa.

$$ f"(x) \le 0 $$

Se applico il criterio di monotonia alla derivata prima, la derivata seconda è sempre minore o uguale a zero se la derivata prima è decrescente.

$$ f"(x) \le 0 \Leftrightarrow f'(x) \:\: \text{ è decrescente} $$

Esempio

La funzione f(x)=log x è concava nel punto x=3 perché la derivata prima f'(x)=1/x è decrescente nell'intorno di x=3.

Se la f'(x) è decrescente allora la derivata seconda f"(x)≤0 nell'intorno di x=3.

E' effettivamente concava in x=3 perché un'eventuale retta tangente della funzione si troverebbe al di sopra della funzione.

Dimostrazione del criterio di convessità e concavità

La dimostrazione si compone in due parti.

1. Se f(x) è convessa, la derivata prima f'(x) è crescente
2. Se la derivata prima f'(x) è crescente, la funzione f(x) è convessa

Nota. Il criterio di concavità si dimostra in modo simile.

Dimostrazione 1

Se f(x) è convessa, la derivata prima f'(x) è crescente

Ho una funzione f(x) definita nell'intervallo [a,b] con due punti dell'intervallo x₁<x₂.

La funzione è convessa, quindi il grafico della funzione f(x) è sempre al di sopra della retta tangente sia in x₁ che in x₂.

$$ f(x) \ge f(x_1)+f'(x_1)(x-x_1) $$

$$ f(x) \ge f(x_2)+f'(x_2)(x-x_2) $$

Dove x è un punto generico di [a,b]

Nota. Il secondo membro delle disequazioni è la retta tangente nel punto x rispetto a x₁ e x₂.

Scelgo di assegnare il punto x=x₂ alla prima disequazione e x=x₁ alla seconda disequazione.

$$ f(x_2) \ge f(x_1)+f'(x_1)(x_2-x_1) $$

$$ f(x_1) \ge f(x_2)+f'(x_2)(x_1-x_2) $$

Dal punto di vista grafico

Sommando membro a membro le disequazioni

$$ f(x_2) + f(x_1) \ge f(x_1)+f'(x_1)(x_2-x_1) + f(x_2)+f'(x_2)(x_1-x_2) $$

$$ 0 \ge - f(x_2) - f(x_1) + f(x_1)+f'(x_1)(x_2-x_1) + f(x_2)+f'(x_2)(x_1-x_2) $$

$$ 0 \ge f'(x_1)(x_2-x_1) +f'(x_2)(x_1-x_2) $$

$$ - f'(x_1)(x_2-x_1) - f'(x_2)(x_1-x_2) \ge 0 $$

Con un semplice passaggio algebrico trasformo (x₁-x₂) in (x₂-x₁)

$$ - f'(x_1)(x_2-x_1) + f'(x_2)(x_2-x_1) \ge 0 $$

Poi metto in evidenza (x₂-x₁)

$$ [ f'(x_2)- f'(x_1) ] \cdot (x_2-x_1) \ge 0 $$

Poiché per definizione iniziale x₂>x₁, il prodotto può essere maggiore o uguale a zero soltanto se f'(x₂)-f'(x₁)>0.

$$ f'(x_2)- f'(x_1) >0 \:\:\: \forall x \in (x_1,x_2) $$

La componente f'(x₂)-f'(x₁)>0 equivale a dire che la derivata prima è crescente nell'intervallo [x₁,x₂].

Per il criterio di monotonia, se la derivata prima è crescente allora la derivata seconda è maggiore o uguale a zero nell'intervallo [x₁,x₂].

$$ f"(x) \ge 0 \:\:\: \forall x \in (x_1,x_2) $$

Questo dimostra che se la funzione è convessa, la derivata prima è crescente e la derivata seconda è maggiore o uguale a zero.

Dimostrazione 2

Provo a dimostrare che è vero anche l'inverso.

Se f'(x) è crescente, allora f(x) è convessa.

Prendo due punti qualsiasi x e x₀ nell'intervallo [a,b] diversi tra loro

$$ x \ne x_0 $$

Secondo il teorema di Lagrange, nell'intervallo esiste un punto x₁ tale che

$$ f'(x_1) = \frac{ f(x)-f(x_0) }{x-x_0} $$

che posso riscrivere in

$$ f(x)-f(x_0) = f'(x_1) \cdot (x-x_0) $$

Per l'ipotesi iniziale la derivata prima f'(x) è crescente nell'intervallo [a,b]

Ora analizzo i due casi

• se x<x₀ allora l'intervallo è (x,x₀) e la componente (x-x₀) è negativa $$ (x-x_0) < 0 $$ poiché il punto x₁ è intermedio nell'intervallo $$ x_1 \in (x,x_0) $$ quindi $$ x_1 < x_0 $$ ed essendo f'(x) crescente allora per il criterio di monotonia anche $$ f'(x_1) \le f'(x_0) $$ Moltiplico entrambi i membri della disequazione per (x-x₀) $$ f'(x_1) \cdot (x-x_0) \le f'(x_0) \cdot (x-x_0) $$ essendo (x-x₀) minore di zero la disequazione diventa $$ f'(x_1) \cdot (x-x_0) \ge f'(x_0) \cdot (x-x_0) $$

  Sapendo che $$ f'(x_1) = \frac{ f(x)-f(x_0) }{x-x_0} $$

  $$ \frac{ f(x)-f(x_0) }{x-x_0} \cdot (x-x_0) \ge f'(x_0) \cdot (x-x_0) $$ $$ f(x)-f(x_0) \ge f'(x_0) \cdot (x-x_0) $$
• se x>x₀ allora l'intervallo è (x₀,x) e la componente (x-x₀) è positiva $$ (x-x_0) > 0 $$ poiché x₁ è intermedio nell'intervallo $$ x_1 \in (x_0,x) $$ quindi $$ x_1 > x_0 $$ ed essendo f'(x) crescente allora anche $$ f'(x_1) \ge f'(x_0) $$ Moltiplico entrambi i membri della disequazione per (x-x₀) $$ f'(x_1) \cdot (x-x_0) \ge f'(x_0) \cdot (x-x_0) $$ In questo caso la componente (x-x₀) è positiva quindi la disequazione non cambia.

  Sapendo che $$ f'(x_1) = \frac{ f(x)-f(x_0) }{x-x_0} $$

  $$ \frac{ f(x)-f(x_0) }{x-x_0} \cdot (x-x_0) \ge f'(x_0) \cdot (x-x_0) $$ $$ f(x)-f(x_0) \ge f'(x_0) \cdot (x-x_0) $$

In entrambi i casi ottengo

$$ f(x)-f(x_0) \ge f'(x_0) \cdot (x-x_0) $$

ossia

$$ f(x) \ge f(x_0) + f'(x_0) \cdot (x-x_0) $$

Dove il secondo membro è l'equazione della retta tangente nel punto x₀.

Essendo f(x) un valore più alto della tangente, il grafico della funzione si trova sopra la tangente.

Pertanto la funzione è convessa.

E così via