La funzione lipschitziana

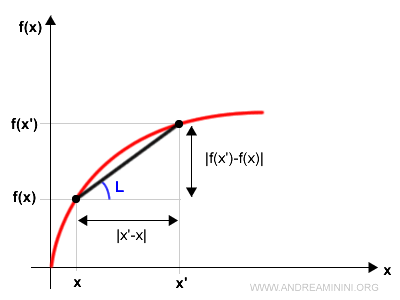
Una funzione f(x) è detta funzione lipschitziana nell'intervallo I di R se esiste una costante L tale che $$ |f(x)-f(x')| \le L |x-x'| $$ per ogni x,x' di I.

Nelle funzioni lipschitziane il tasso di crescita sulle ordinate è limitato da una costante L detta costante di Lipschitz.

Si tratta di una condizione più forte della continuità.

Cosa significa?. Dal punto di vista geometrico vuol dire che dati due punti qualsiasi dell'intervallo il coefficiente angolare della retta che congiunge i due punti deve essere sempre minore uguale a L.

Le funzioni lipschitziane sono state formalizzate dal matematico tedesco Rudolph Otto Sigismund Lipschitz

Come riconoscere le funzioni di Lipschitz

Se la funzione f(x) è derivabile nell'intervallo I, allora la funzione f(x) è lipschitziana in I con costante L, se e solo il valore assoluto della derivata è minore o uguale a L per ogni x di L $$ |f'(x)| \le \:\:\: \forall x \in L $$

In pratica, se la funzione derivabile nell'intervallo considerato è una funzione limitata allora è lipschitziana.

Dimostrazione

Se vale la seguente per ogni x dell'intervallo I

$$ |f'(x)| \le L $$

Applicando il teorema di Lagrange tra gli estremi [x,x'] di I

$$ |f(x)-f(x')|= |f'(x_0)(x-x')| \le L \cdot |x-x'| $$

Pertanto, la derivata deve essere inferiore a L

Considerando x'=x+h

$$ |f(x)-f(x')| \le L \cdot |x-x'| $$

$$ |f(x)-f(x+h)| \le L \cdot |x-(x+h)| $$

$$ |f(x)-f(x+h)| \le L \cdot |h| $$

per il valore assoluto vale anche

$$ |f(x+h)-f(x)| \le L \cdot |h| $$

Divido entrambi i membri per h

$$ \frac{ |f(x+h)-f(x)| }{|h|} \le L \cdot \frac{ |h| }{ |h| } $$

$$ \frac{ |f(x+h)-f(x)| }{|h|} \le L $$

Infine calcolo il limite per h tendente a zero e ottengo la derivata prima della funzione nel punto x.

$$ \lim_{h \rightarrow 0 } \frac{ |f(x+h)-f(x)| }{|h|} = f'(x) \le L $$

Nota. La condizione delle funzioni lipschitziane $$ |f(x)-f(x_0)| \le L |x-x_0| $$ posso riscriverla in questo modo $$ \frac{|f(x)-f(x_0)|}{|x-x_0|} \le L $$ Dal punto di vista geometrico, il rapporto incrementale tra due punti è uguale al coefficiente angolare della retta che congiunge i due punti.

Il limite del rapporto incrementale per h→0 è la derivata della funzione nel punto x₀. $$ f'(x) = \lim_{h \rightarrow 0} \frac{|f(x_0+h)-f(x_0)|}{|h|} \le L $$ Pertanto se la derivata prima della funzione in ogni punto x dell'intervallo I è minore di L, posso affermare che la funzione è lipschitziana

Un esempio pratico

_{Esempio 1}

La funzione f(x)=x² è lipschitziana per L=8 nell'intervallo [0,4]

$$ f(x)=x^2 $$

Essendo una funzione derivabile, calcolo la derivata

$$ f'(x)=2x $$

poi calcolo la pendenza (coefficiente angolare) della funzione f(x) tra i due punti x₀=0 e x₁=4 tramite la sua derivata.

$$ |f'(x1)-f'(x0)|=|2(4)-2(0)|=|8| $$

Pertanto, nell'intervallo [0,4] la funzione è limitata perché il suo coefficiente angolare è inferiore a 8.

$$ |f'(x_1)-f'(x_0)| \le 8 \cdot |x_1-x_0| $$

ossia

$$ \frac{ |f'(x_1)-f'(x_0)| } { |x_1-x_0| } \le 8 $$

Il grafico della funzione rende tutto più chiaro

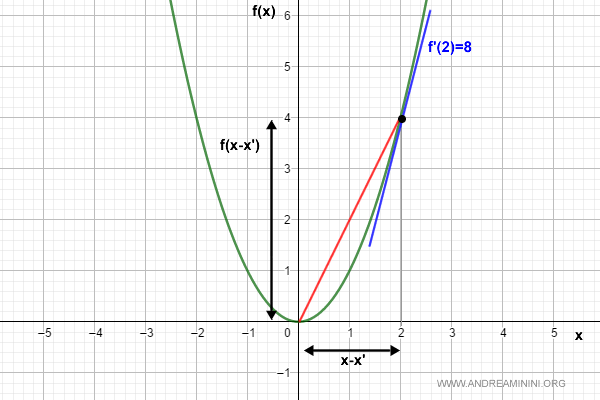
Nell'intervallo [0,2] qualsiasi retta tangente alla funzione ha un coefficiente angolare minore di 8.

Quindi, la funzione f(x)=x² è lipschitziana nell'intervallo per L=8 ( costante di Lipschitz ).

Esempio 2

La funzione seno è lipschitziana in R con L=1

$$ f(x) =\sin x $$

Per dimostrarlo basta calcolare la derivata

$$ f'(x) = | \cos x | $$

La derivata prima del seno è sempre minore o uguale a L per ogni x ∈ R

Uniforme continuità delle funzioni lipschitziane

La funzione lipschitziana è anche uniformemente continua nell'intervallo I.

Fissato un ε>0 e δ=ε/L

$$ ε>0 \\ δ=ε/L $$

La condizione di uniforme continuità nell'intervallo I è sempre soddisfatta

$$ \forall x,y \in I \Rightarrow |f(x)-f(x')|<ε, |x-x'|<δ $$

perché nella funzione lipschitziana

$$ |f(x)-f(x')|<L|x-x'| $$

Quindi, risulta |f(x)-f'(x)|<ε per qualsiasi coppia di punti (x,x') tali che |x-x'|<δ

Attenzione. Non vale il contrario. Se una funzione è uniformemente continua, non è detto che sia anche lipschitziana.

Un esempio pratico

Questa funzione è uniformemente continua nell'intervallo [0,1]

$$ f(x) = \sqrt{x} $$

Nell'intervallo [0,1] non è una funzione lipschitziana perché la derivata f'(x) tende a infinito per x tendente a 0.

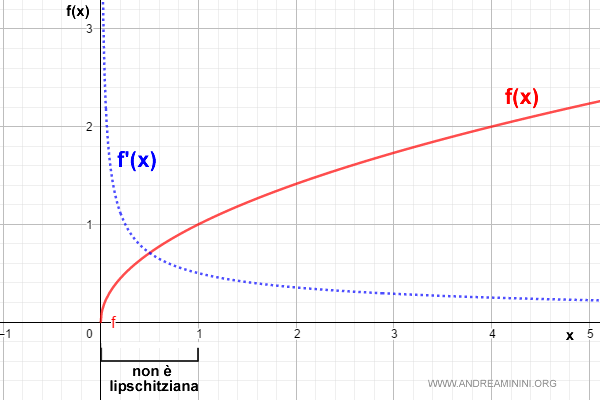
Quindi, non esiste nessun valore L tale da soddisfare la proprietà delle funzioni lipschitziane nell'intervallo [0,1]

Nota. La stessa funzione è invece lipschitziana nell'intervallo [1,∞] perché è possibile individuare dei valori di L che delimitano la crescita della funzione.

E così via.