Funzione sinusoidale

Le funzioni sinusoidali sono funzioni basate sulla funzione seno o coseno. $$ y=A \cdot \sin (\omega x + \phi) $$ $$ y=A \cdot \cos (\omega x + \phi) $$ Dove A è l'ampiezza della sinusoide, ω (omega) è la pulsazione (radianti al secondo) e φ (phi) è la fase iniziale. $$ A, \omega, \phi \in R $$

Le due formule sono equivalenti se si considera che il coseno è il seno sfasato di π/2 (90°)

$$ y= A \cdot \cos (\omega x + \phi ) =A \cdot \sin (\omega x + \phi + \frac{\pi}{2}) $$

Dal punto di vista grafico la differenza tra seno e coseno è subito evidente.

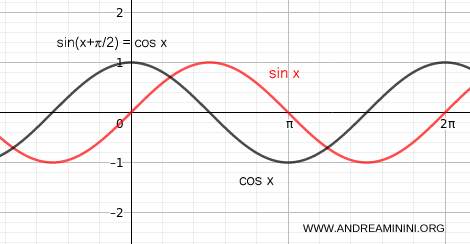
E viceversa il seno è il coseno sfasato di -π/2 (-90°)

$$ y= A \cdot \sin (\omega x + \phi ) =A \cdot \cos (\omega x + \phi - \frac{\pi}{2}) $$

Un altro modo per scrivere l'equivalenza tra seno e coseno è la seguente

$$ \sin x = \cos(x - \frac{\pi}{2}) = \cos(\frac{\pi}{2}-x) $$

$$ \cos x = \sin(x + \frac{\pi}{2}) = \sin(\frac{\pi}{2}-x) $$

Quindi, qualsiasi funzione sinusoidale posso costruirla sul seno o sul coseno a seconda della convenienza algebrica nei calcoli.

Nota. La scelta del seno o del coseno varia caso per caso. Spesso, la scelta di uno o dell'altro mi consente di semplificare un'espressione algebrica.

A cosa servono?

Le funzioni sinusoidali sono utili per studiare molti fenomeni fisici.

Ad esempio, in fisica sono usate per descrivere il moto circolare o il moto armonico di un corpo, la corrente elettrica alternata, un segnale sinusoidale nelle telecomunicazioni.

Nota. Tramite l'analisi di Fourier si può descrivere qualsiasi segnale periodico complesso come somma di sinusoidi.

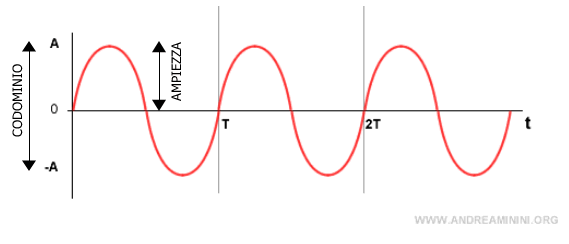
L'ampiezza

L'ampiezza |A| della funzione sinusoidale determina l'altezza del grafico e il codominio della funzione sinusoidale [-A , A].

La pulsazione (o frequenza angolare)

La frequenza angolare (o pulsazione) misura i radianti al secondo e dipende dal periodo T della sinusoide.

$$ \omega = \frac{2 \pi}{T} $$

Poiché tra il periodo T e la frequenza f c'è una nota relazione inversa

$$ f = \frac{1}{T} $$

posso anche scrivere la pulsazione ω in questa forma equivalente

$$ \omega = 2 \pi f $$

Quanti più radianti o periodi (T) compie la funzione sinusoidale in un secondo, tanto maggiore è la sua frequenza angolare o pulsazione ω in rad/s.

Nota. Al denominatore ho posto 2π per indicare i radianti compreso in 360° ossia in un giro completo dell'angolo nella circonferenza di un cerchio.

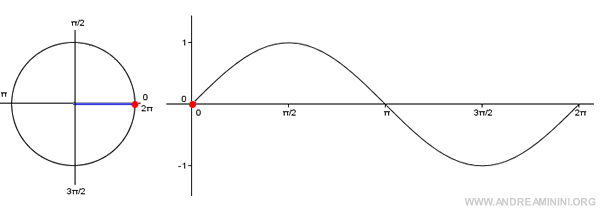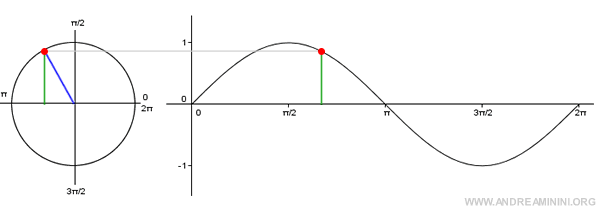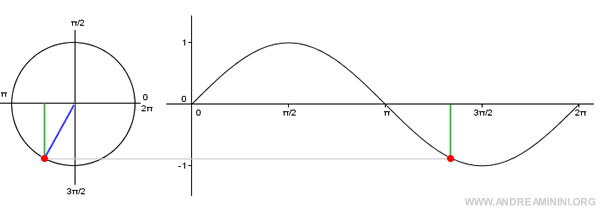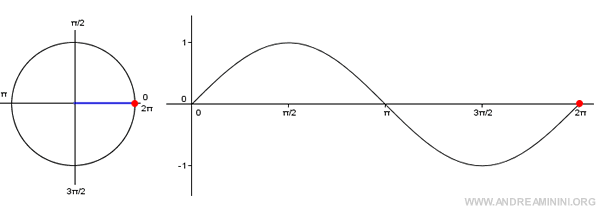
L'argomento della sinusoide ωt è uguale a 2π se t=1.

$$ \omega t = 2 \pi $$

In questi due grafici l'equivalente ωt=2π è ben evidente.

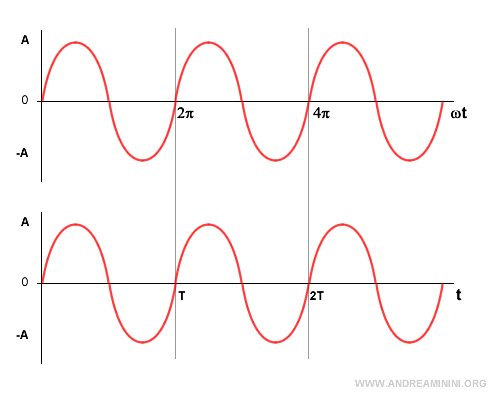
Se aumento la frequenza angolare, la funzione compie un maggior numero di pulsazioni (radianti) in un secondo.

Ad esempio, prendo due funzioni sinusoidali.

La funzione rossa compie ω=2 pulsazioni in un secondo, la funzione blu compie ω=4 pulsazioni in un secondo.

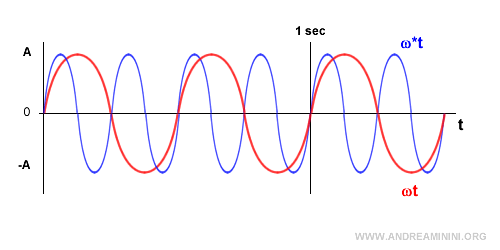
Pertanto, la funzione blu ha una velocità angolare maggiore della funzione rossa (ω*>ω). In un secondo compie più "giri" ossia percorre più radianti.

In questo caso, la funzione blu ha il doppio della velocità angolare della funzione rossa (ω*=2ω).

Ne consegue che una variazione ω delle pulsazioni modifica il periodo T della funzione sinusoidale.

$$ T = \frac{2 \pi}{\omega} $$

Il periodo

Una funzione sinusoidale è una periodica. Quindi, si ripete nel tempo. $$ y(t) = y(t+T) $$

Ad esempio, nell'istante t₁ e nell'istante t₁+T la funzione sinusoidale assume lo stesso valore y(t₁)=y(t₁+T)=-A.

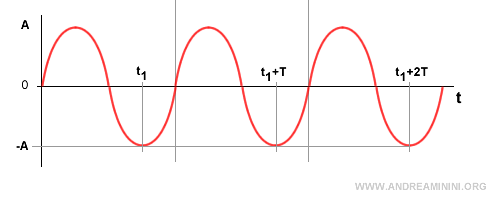
Lo stesso vale per ogni multiplo di T ossia y(t₁)=y(t₁+kT)=-A dove k=1,2,3,... e via dicendo

$$ y(t) = y(t+kT) \ \ \ \ k=1,2,3,... $$

In generale, considerando anche le pulsazioni ω e la fase iniziale φ la formula periodica di una sinusoide posso scriverla in questo modo

$$ y = \sin(x+kT) $$

$$ y = \sin ( \omega (x+kT) + \phi) $$

Una qualsiasi variazione del coefficiente angolare ω (pulsazioni) modifica il periodo.

Sapendo che T=2π/ ω, un aumento delle pulsazioni (Δω>0) riduce il periodo T della funzione.

$$ T = \frac{2 \pi}{ \omega} $$

Viceversa una diminuzione delle pulsazioni (Δω<0) aumenta il periodo T.

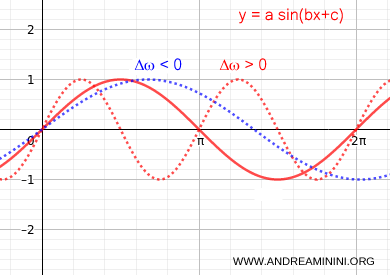
Nota. La variazione della fase (sfasamento) invece non modifica il periodo T della funzione sinusoidale.

La contrazione e dilatazione delle funzioni sinusoidale

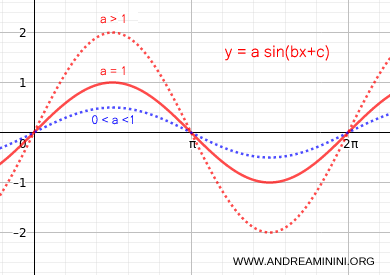
Ogni funzione sinusoidale può essere generalizzata tramite questa formula $$ y = a \sin (b \cdot x + c ) $$

• Il coefficiente a determina una dilatazione verticale (a>1) o una contrazione verticale (0<a<1) dell'ampiezza.
  
• Il coefficiente b determina una dilatazione orizzontale (0<b<1) o una contrazione orizzontale (b>1) del grafico della funzione sinusoidale. Il cambiamento del coefficiente b (detto pulsazione ω) modifica il periodo (T) della funzione.
  

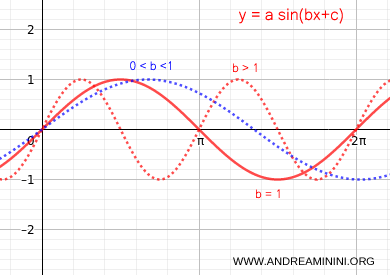
  Nota. In pratica, se il coefficiente b>1 la velocità angolare aumenta e la funzione percorre più radianti in un secondo (più pulsazioni). Viceversa, se 0<b<1 la velocità angolare si riduce e la funzione percorre meno radianti in un secondo (meno pulsazioni).

• Il coefficiente c determina una traslazione orizzontale indietro (c>0) o in avanti (c<0) del grafico della funzione sinusoidale. La variazione del coefficiente c è detta sfasamento.
  

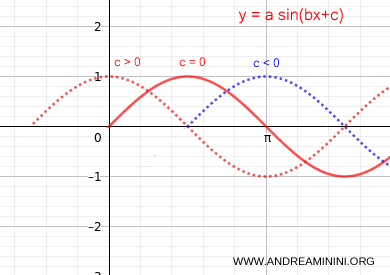
  Nota. Nella teoria dei segnali la traslazione indietro (c>0) della funzione sinusoidale è detta anticipo perché il periodo del seno comincia prima dello zero. La traslazione in avanti (c<0) è invece detta ritardo perché il periodo del seno comincia dopo lo zero.

E così via.