Dilatazione e contrazione di una funzione
Una dilatazione è una trasformazione geometrica che modifica la forma grafica di una funzione nel piano cartesiano, senza alterarne la simmetria né la posizione dell’origine.
La trasformazione della funzione agisce su uno dei due assi: orizzontale (x) o verticale (y).
A seconda del valore del parametro, si ha una dilatazione se il grafico si espande oppure una contrazione se si restringe.
Dilatazione orizzontale
Una dilatazione orizzontale si verifica quando si modifica la variabile indipendente $x$ all’interno della funzione.
$$ y = f\left( \dfrac{x}{m} \right) \quad \text{con } m > 1 $$
Il grafico si allarga orizzontalmente rispetto all’origine $O$. Ogni punto della funzione viene "spinto" più lontano lungo l’asse $x$.
Esempio
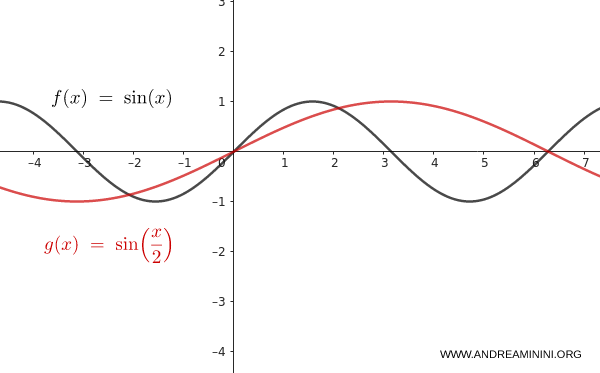
Considero la funzione $f(x) = \sin(x)$.
Applico la dilatazione orizzontale con $m = 2$:
$$ y = \sin\left( \dfrac{x}{2} \right) $$
Il periodo raddoppia: la sinusoide impiega il doppio dello spazio per ripetersi. Si è verificata una dilatazione orizzontale.
Contrazione orizzontale
Una contrazione orizzontale si verifica quando il grafico si restringe orizzontalmente.
$$ y = f\left( \dfrac{x}{m} \right) \quad \text{con } 0 < m < 1 $$
Tutti i punti si avvicinano all’asse $y$.
Esempio
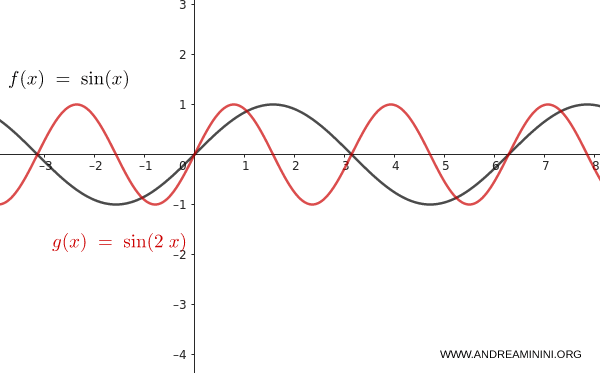
Uso ancora la funzione $f(x) = \sin(x)$.
Applico la contrazione orizzontale con $m = \frac{1}{2}$:
$$ y = \sin(2x) $$
Il periodo si dimezza: la funzione si ripete due volte più rapidamente. È avvenuta una contrazione orizzontale.
Dilatazione verticale
Una dilatazione verticale agisce sull’intera funzione, moltiplicandola per un coefficiente $n$:
$$ y = n \cdot f(x) \quad \text{con } n > 1 $$
Il grafico si allunga verso l’alto e verso il basso rispetto all’asse $x$. Tutti i valori di $y$ diventano più grandi in modulo.
Esempio
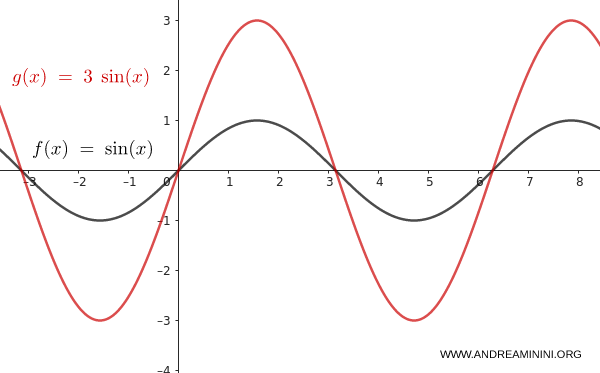
Prendo la funzione $f(x) = \sin(x)$.
Applico una dilatazione verticale con $n = 3$:
$$ y = 3 \cdot \sin(x) $$
L’ampiezza dell’onda triplica: passa da 1 a 3. La forma resta la stessa, ma il grafico si allunga verticalmente.
Contrazione verticale
Una contrazione verticale si ha quando:
$$ y = n \cdot f(x) \quad \text{con } 0 < n < 1 $$
In questo caso l’ampiezza del grafico della funzione si riduce.
Esempio
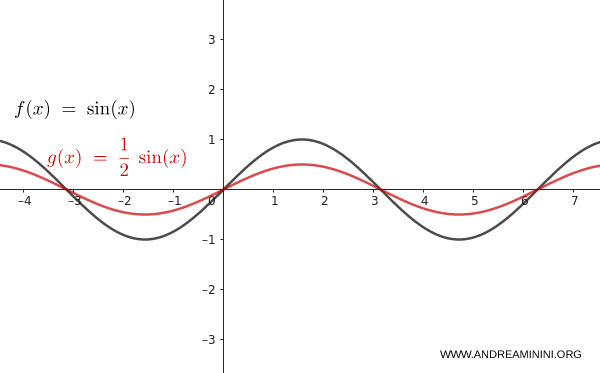
Prendo $f(x) = \sin(x)$.
Applico una contrazione verticale con $n = \frac{1}{2}$:
$$ y = \dfrac{1}{2} \cdot \sin(x) $$
L’ampiezza si riduce da 1 a 0,5. Il grafico si comprime verticalmente.
E così via.
