Funzione quadratica
Una funzione quadratica è definita dall'espressione del tipo $$ y = ax^2+ bx + c $$ dove il primo coefficiente a≠0 è sempre diverso da zero.
Il grafico di una funzione quadratica è una parabola.
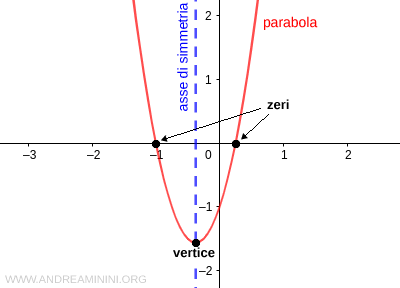
L'asse di simmetria della parabola è una retta verticale
$$ x = - \frac{b}{2a} $$
Il vertice della parabola è il punto V
$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} $$
Gli zeri della funzione quadratica sono i valori della x in cui la parabola interseca l'asse delle ascisse. Sono detti zeri perché in questi punti il valore della funzione quadratica è zero y=0.
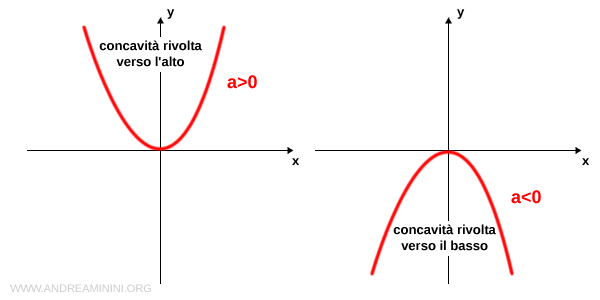
La concavità della parabola dipende solo dal segno del primo coefficiente (a)
- a>0
Se il segno del primo coefficiente è positivo (a>0) la parabola ha la concavità rivolta verso l'alto. - a<0
Se il segno del primo coefficiente è negativo (a<0) la parabola ha la concavità rivolta verso il basso.
L'apertura della parabola dipende solo dal modulo (valore assoluto) del primo coefficiente (a)
Quanto maggiore è il valore assoluto |a|, tanto più stretta è l'apertura della parabola.
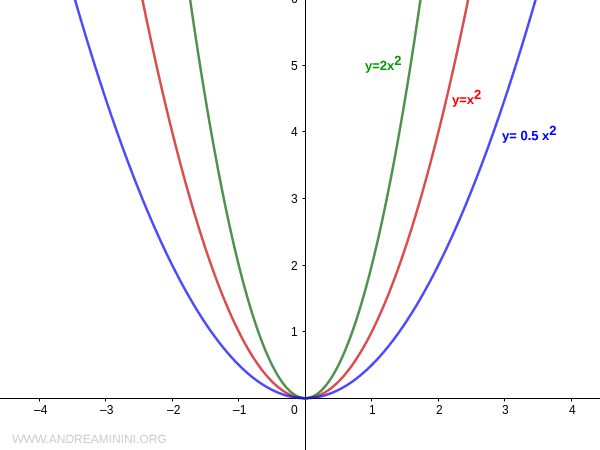
Nota. Per apertura della parabola intendo la distanza tra il grafico della parabola e l'asse di simmetria. Pertanto, una riduzione del valore assoluto |a| avvicina il grafico della parabola all'asse di simmetria della parabola.
Un esempio pratico
Considero la funzione quadratica
$$ y = 4x^2 + 3x -1 $$
Il coefficiente a=4 è positivo, quindi la parabola ha la concavità rivolta verso l'alto.
Per trovare gli zeri della funzione (intersezioni con l'asse x) devo risolvere l'equazione di 2° grado associata
$$ 4x^2 + 3x -1 = 0 $$
Il discriminante è positivo.
$$ \Delta = b^2- 4ac = 3^2 - 4(4)(-1) = 9 + 16 = 25 $$
Pertanto, l'equazione ha due soluzioni reali distinte
$$ x = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-3 \pm \sqrt{25} }{2(4)} = \frac{-3 \pm, 5}{8} = \begin{cases} x_1 = \frac{-3-5}{8} = -1 \\ \\ x_2 = \frac{-3+5}{8} = \frac{1}{4} \end{cases} $$
Gli zeri della funzione quadratica sono x1=1 = -1 e x2 = 1/4
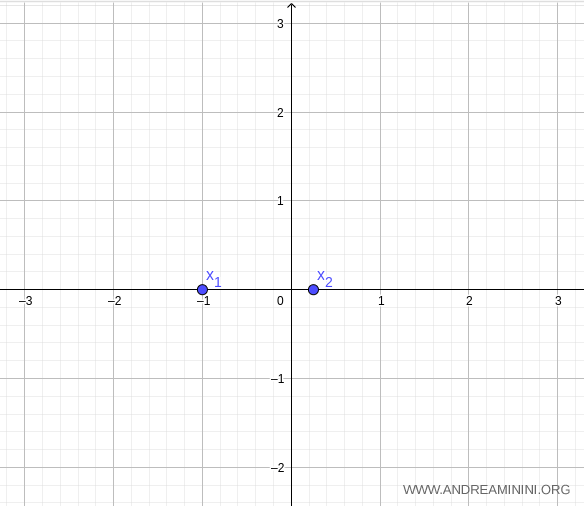
Calcolo l'asse di simmetria della parabola sapendo che a=4, b=3, c=-1
$$ x = - \frac{b}{2a} = - \frac{3}{2 \cdot 4} = - \frac{3}{8} $$
L'asse di simmetria della parabola è la retta verticale perpendicolare all'asse x nel punto x=-3/8
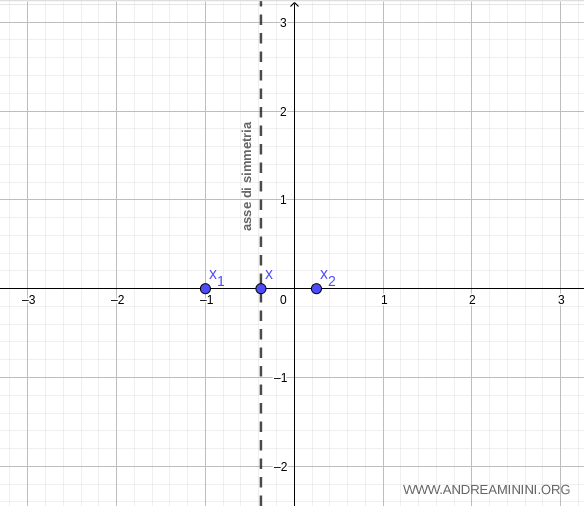
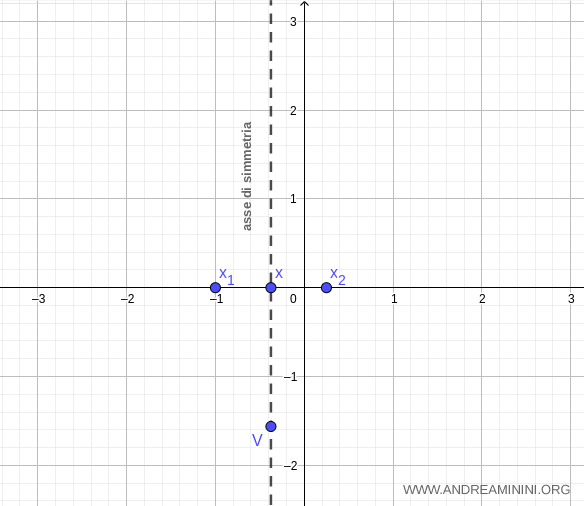
Calcolo il vertice della parabola
$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} = \begin{pmatrix} - \frac{3}{8} ; - \frac{25}{16} \end{pmatrix} $$
Il vertice della parabola è il punto V (-3/8, -25/16)
Per disegnare gli altri punti della parabola calcolo il valore della y nei punti x intorno l'asse di simmetria.
Sapendo che y=4x2+3x-1
$$ \begin{array}{c|lcr} x & y \\ \hline -2 & 9 \\ -1 & 0 \\ 0 & -1 \\ 1 & 6 \end{array} $$
Questo mi permette di tracciare il grafico della parabola
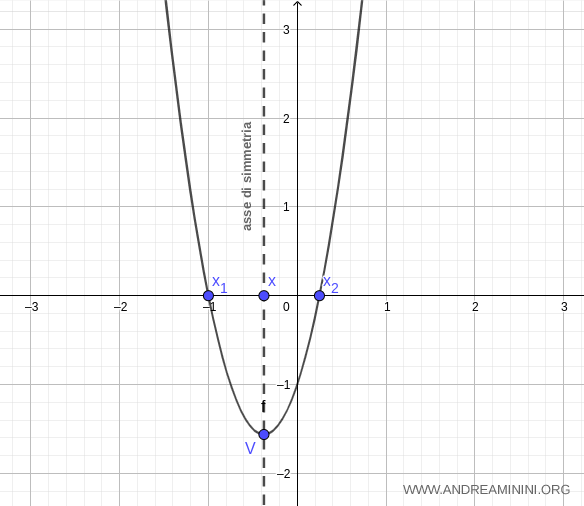
E così via.
