Il dominio di una funzione

Il dominio di una funzione è l’insieme $ A $ dei valori della variabile indipendente per i quali la funzione è definita. $$ f:A \rightarrow B $$ Il dominio A è l'insieme di partenza della funzione. L'insieme B è l'insieme di arrivo ed è detto codominio della funzione

In altre parole, il dominio è l’insieme dei valori per cui l’espressione della funzione ha senso dal punto di vista matematico.

Questo insieme prende il nome di dominio naturale o campo di esistenza della funzione.

In genere, quando si parla semplicemente di dominio, ci si riferisce proprio al dominio naturale, cioè a quello che deriva direttamente dall’espressione analitica della funzione, senza imporre ulteriori limitazioni.

La differenza tra dominio e insieme di definizione. In questa definizione il dominio e l’insieme di definizione coincidono e rappresentano l’insieme dei valori per cui la funzione è definita. In alcuni libri, tuttavia, viene fatta una distinzione tra i due concetti: il dominio è inteso come un insieme assegnato a priori, mentre l’insieme di definizione è il sottoinsieme del dominio formato solo dai valori per cui l’espressione della funzione ha effettivamente senso. Lo cito solo per completezza.

A scuola si studiano soprattutto funzioni con dominio contenuto nei numeri reali, ma esistono anche funzioni definite su altri insiemi numerici, ad esempio sui numeri complessi.

Un esempio pratico

Condidero due insiemi finiti X e Y

$$ X = \{1,2,3,4,5 \} $$

$$ Y = \{1,2,3,4,5,6,7,8,9 \} $$

e la relazione definita dalla legge

$$ f: y = x^2 $$

Non tutti gli elementi di $ X $ vengono associati a un elemento di $ Y $. Ad esempio, $ 4^2 = 16 \not \in Y $.

Quindi la funzione è definita solo per $ f(1)=1 $, $ f(2)=4 $, $ f(3)=9 $:

$$ D_f = \{1,2,3 \} \subseteq X $$

L'insieme $ D_f $ è detto insieme di definizione (o dominio) della funzione.

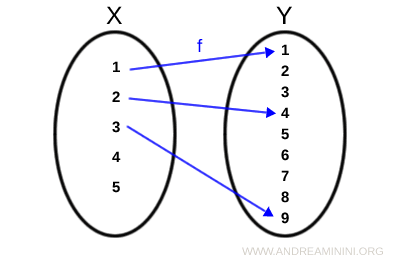
Quindi, la funzione è $ f:D_f \rightarrow Y $ con $ f(1)=1 $, $ f(2)=4 $, $ f(3)=9 $.

Nota. Come anticipato, in questa pagina non distinguo tra dominio e insieme di definizione: li considero sinonimi. Di conseguenza, $ D_f $ rappresenta sia il dominio che l'insieme di definizione della funzione. Nei libri in cui si distingue tra dominio e insieme di definizione, invece, l'insieme $ X $ viene considerato come il dominio della funzione, quello fissato a priori, mentre l'insieme $ D_f = \{1,2,3 \} $ rappresenta l'insieme di definzione, cioè l’insieme dei valori per cui la funzione ha effettivamente senso. Tutto dipende dalla notazione che si sceglie.

Esempio 2

Considero la funzione reale

$$ f: y = \sin(x) $$

Sia il dominio che il codominio corrispondono all'insieme dei numeri reali

$$ f: R \rightarrow R $$

Anche in questo caso il dominio (o insieme di definizione) è l’insieme dei valori per cui la funzione ha senso.

E così via.