La funzione esponenziale
La funzione esponenziale è una funzione del tipo $$ y = a^x $$ dove la base a>0 è un numero reale positivo. $$ a \in R^+ $$
Il dominio della funzione è l'insieme dei numeri reali.
Il codominio della funzione è l'insieme dei numeri reali positivi.
$$ f:R \rightarrow R^+ $$
Il grafico della funzione esponenziale varia a seconda dell'esponente e della base.
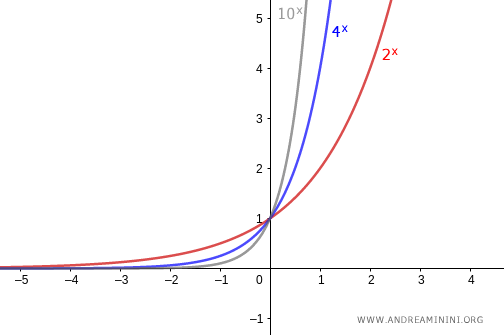
- Se la base è maggiore di uno (a>1) il grafico della funzione esponenziale è strettamente crescente. E' una funzione biettiva.
- Se la base è uguale a uno (a=1) il grafico della funzione esponenziale è costante e pari a uno. E' una funzione non iniettiva.
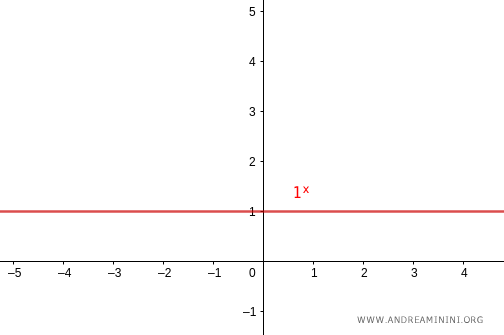
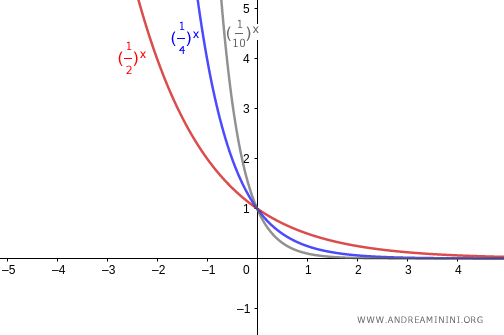
- Se la base è compresa tra zero e uno (0<a<1) il grafico della funzione esponenziale è strettamente decrescente. E' una funzione biettiva.
Nota. In tutti i casi il grafico della funzione interseca l'asse delle ordinate nel punto (0;1) e non interseca mai l'asse dell'ascissa. La funzione è sempre positiva ed è una funzione continua.
E così via.
