Gli asintoti
Cosa sono gli asintoti
In matematica un asintoto è una retta (o una curva) che si avvicina al grafico della funzione in modo indefinito quando la variabile indipendente x tende a più o meno infinito.
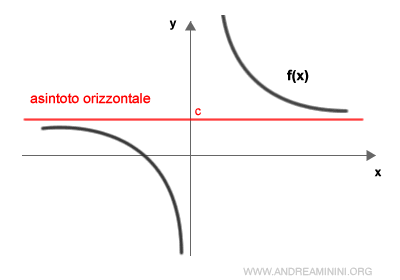
In pratica, la distanza tra l'asintoto e il grafico della funzione tende a zero.
- Se l'asintoto è una retta si parla di retta asintotica.
- Se l'asintoto è una curva si parla di curva asintotica.
Esistono tre tipologie di asintoti: orizzontali, verticali e obliqui.
L'asintoto orizzontale
L'asintoto orizzontale si calcola con il limite della funzione per x tendente a +∞ o -∞
$$ \lim_{x \rightarrow ±∞ } f(x) = c $$
L'asintoto orizzontale esiste se il limite esiste ed è un numero reale finito.
Ecco un esempio pratico di asintoto orizzontale.

In pratica, l'asintoto orizzontale è una retta parallela o coincidente all'asse dell'ascisse.
Ovviamente gli asintoti orizzontali per x tendente a +∞ e a -∞ possono anche non coincidere.
Esempio
Devo calcolare gli asintoti orizzontali della funzione
$$ f(x) = \frac{x+1}{x} $$
Calcolo il limite per x tendente a +∞
$$ \lim_{x \rightarrow +∞ }\frac{x+1}{x} = 1 $$
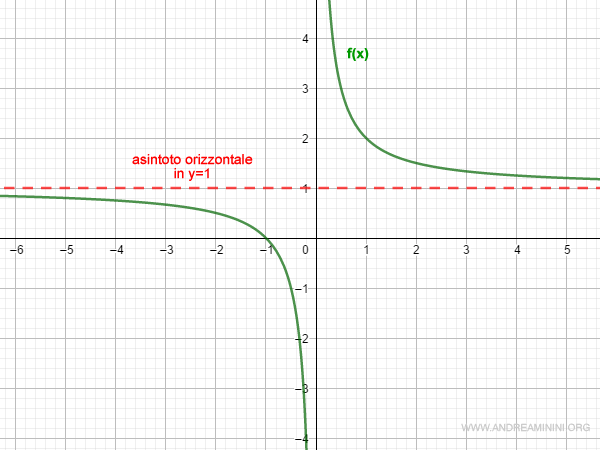
Quindi, la funzione ha un asintoto orizzontale in y=1 per x→+∞
Nota. E' una forma indeterminata di limite ∞/∞ che si risolve facilmente con il teorema di L'Hopital.
Ora calcolo il limite per x tendente a -∞
$$ \lim_{x \rightarrow -∞ }\frac{x+1}{x} = 1 $$
Pertanto, la funzione ha un asintoto orizzontale in y=1 per x→-∞
L'asintoto verticale
L'asintoto verticale si calcola nei punti in cui la funzione non è definita con il limite per x tendente x0 da destra e da sinistra. $$ \lim_{x \rightarrow x_0^+ } f(x) = ±∞ $$ $$ \lim_{x \rightarrow x_0^- } f(x) = ±∞ $$ Dove x0 è un punto in cui la funzione non è definita.
L'asintoto verticale esiste in x0 se il limite è più o meno infinito.
Ecco un esempio pratico di asintoto verticale.
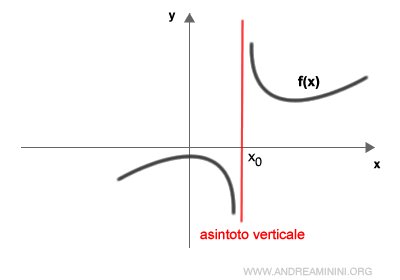
In pratica, l'asintoto verticale è una retta parallela o coincidente all'asse delle ordinate.
Esempio
Devo verificare se la funzione ha asintoti verticali
$$ f(x) = \frac{x^2}{x-1} $$
La funzione è indefinita per x=1.
Quindi, calcolo il limite per x0=1 da destra e da sinistra.
$$ \lim_{x \rightarrow 1^+ } \frac{x^2}{x-1} = +∞ $$
$$ \lim_{x \rightarrow 1^- } \frac{x^2}{x-1} = -∞ $$
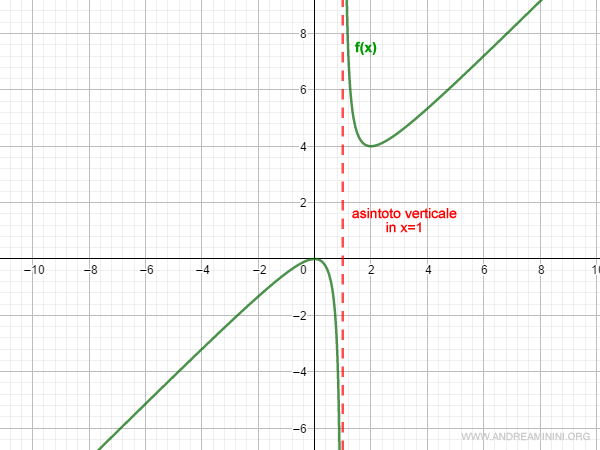
Ho così trovato l'asintoto verticale in x0=1
L'asintoto obliquo
L'asintoto obliquo esiste se il limite per x tendente a +∞ o -∞ della differenza tra la funzione f(x) e la retta y=mx+q è uguale a zero $$ \lim_{x \rightarrow ±∞ } f(x) - (mx+q) = 0 $$
Ecco un esempio pratico di asintoto obliquo
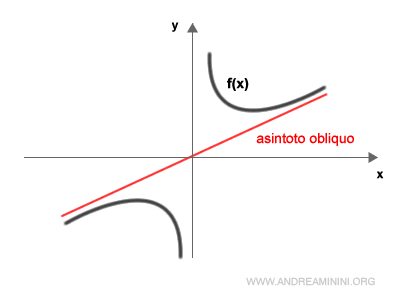
Per verificare l'esistenza di un asintoto obliquo per x tendente a +∞, individuo il coefficiente angolare m della retta.
$$ m = \lim_{x \rightarrow +∞ } \frac{f(x)}{x} \ne 0 $$
Dimostrazione. Se $$ \lim_{x \rightarrow +∞ } f(x) - (mx+q) = 0 $$ per determinare il coefficiente angolare annullo il termine noto q=0. $$ \lim_{x \rightarrow +∞ } f(x) - mx = 0 $$ Essendo il limite uguale a zero per x→∞, non cambia se divido tutto per x. $$ \lim_{x \rightarrow +∞ } \frac{f(x) - mx}{x} = 0 $$ $$ \lim_{x \rightarrow +∞ } \frac{f(x)}{x} - m = 0 $$ $$ \lim_{x \rightarrow +∞ } \frac{f(x)}{x} = m $$
Se il coefficiente angolare m esiste ed è diverso da zero, calcolo un secondo limite per individuare il termine noto q della retta.
$$ q= \lim_{x \rightarrow ±∞ } f(x) - mx \ne ∞ $$
Dimostrazione. Se $$ \lim_{x \rightarrow +∞ } f(x) - (mx+q) = 0 $$ allora $$ \lim_{x \rightarrow +∞ } f(x) - mx - q = 0 $$ $$ \lim_{x \rightarrow +∞ } f(x) - mx = q $$
Se il termine noto q esiste ed è diverso da infinito, allora la funzione ha un asintoto obliquo y=mx+q per x tendente a +∞. In caso contrario non ce l'ha.
Con la stessa procedura verifico anche l'esistenza dell'asintoto obliquo per x tendente a -∞.
Esempio
Devo verificare se la funzione ha un asintoto obliquo
$$ f(x) = \frac{x^2}{x-1} $$
Per prima cosa verifico se il limite per x tendente a infinito è infinito.
$$ \lim_{x \rightarrow ∞} \frac{x^2}{x-1} = ∞ $$
Nota. Si tratta di una forma indeterminata di limite ∞/∞ che si risolve facilmente con il teorema di L'Hopital.
Quindi, verifico se esiste il coefficiente angolare diverso da zero.
$$ m = \lim_{x \rightarrow ∞} \frac{ \frac{x^2}{x-1} }{x} $$
$$ m = \lim_{x \rightarrow ∞} \frac{x^2}{x(x-1)} $$
$$ m = \lim_{x \rightarrow ∞} \frac{x}{(x-1)} = 1 $$
Il coefficiente angolare m=1 esiste ed è diverso da zero.
A questo punto verifico se l'intercetta è diversa da ±∞.
$$ q = \lim_{x \rightarrow ∞} \frac{x^2}{x-1} - mx $$
poiché m=1
$$ q = \lim_{x \rightarrow ∞} \frac{x^2}{x-1} - x $$
$$ q = \lim_{x \rightarrow ∞} \frac{x^2-x^2+x}{x-1} $$
$$ q = \lim_{x \rightarrow ∞} \frac{x}{x-1} = 1 $$
Ho così trovato il coefficiente angolare m=1 e l'intercetta q=1 della retta asintotica obliqua.
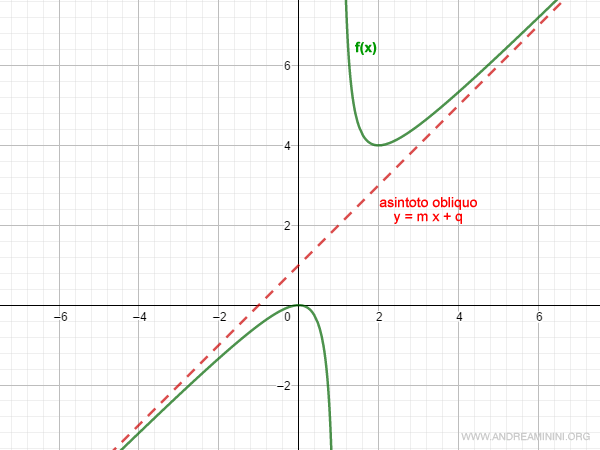
E così via.
