Linee di livello
Le linee di livello di una funzione di due variabili z=f(x,y) è un insieme di punti (x,y) del piano che soddisfano l'equazione f(x,y)=k. Dove k indica la quota, ossia l'altezza o la profondità della funzione sull'asse z.$$ \{ \ (x,y) \in R^2 \ | \ f(x,y)=k \ \} $$
Le linee di livello sono un sottoinsieme dello spazio della funzione z=f(x,y).
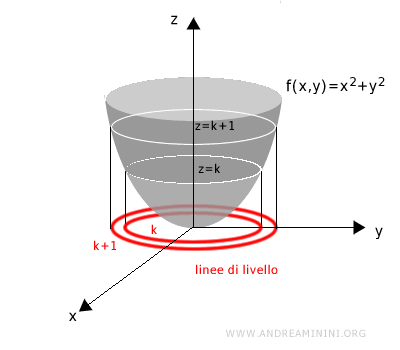
Sono utili per rappresentare il grafico di una funzione a due o più variabili in modo più semplice e comprensibile.
Come costruire le linee di livello
Disegno il grafico di una funzione di due variabili z=f(x,y).
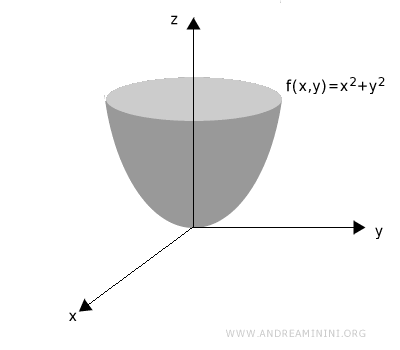
Per individuare una linea di livello k, interseco il grafico della funzione con un piano parallelo al piano xy ad altezza o profondità x=k.
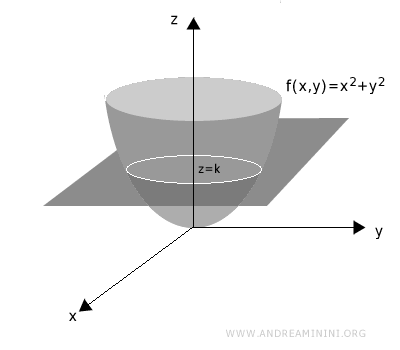
Poi proietto i punti di intersezione sul piano xy.
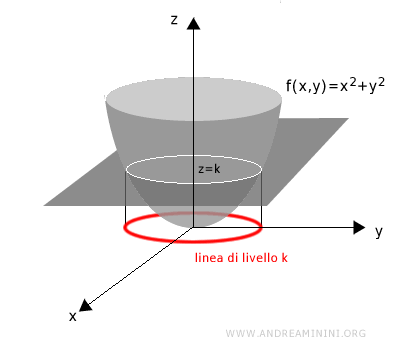
La proiezione sul piano xy è detta linea di livello k. Le linee di livello si trovano sempre sul piano xy.
Ripeto la stessa operazione a diverse altezze e profondità, ottendendo altre linee di livello.

Le linee di livello sono utili perché danno un'idea del comportamento della funzione utilizzando il piano a due dimensione.
Un esempio pratico
Prendo in considerazione la funzione a due variabili
$$ z= f(x,y)=x^2+y^2 $$
Il grafico della funzione nello spazio a 3 dimensioni (x,y,z) è il seguente
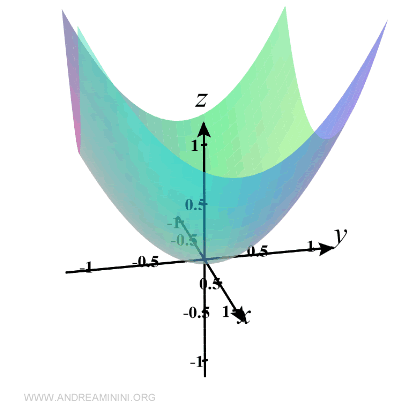
Ora trovo le varie linee di livello che mi interessa rappresentare
$$ x^2 + y^2 = k $$
Le linee di livello k<0 non esistono, perché la funzione f(x,y) non assume valori negativi.
La linea di livello k=0 coincide con l'origine (0,0) del piano cartesiano.
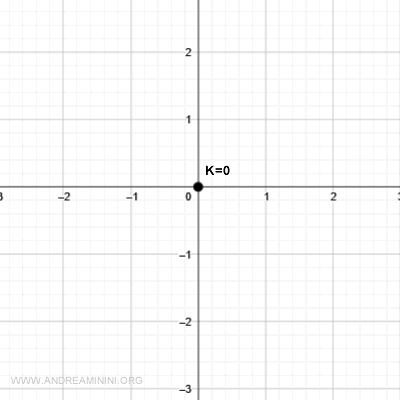
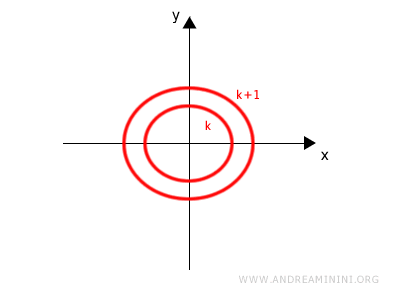
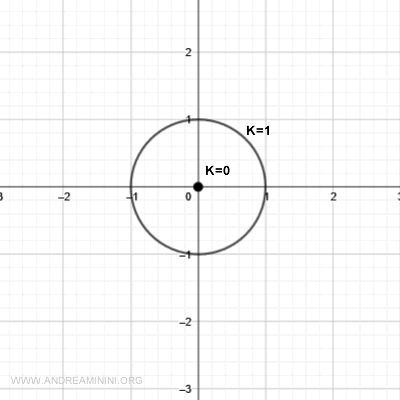
La linea di livello k=1 è una circonferenza di raggio k che si ottiene quando
$$ x^2 + y^2 = 1 $$
Dal punto ti vista grafico è un piano che interseca il grafico della funzione all'atezza z=k=1.
La linea di livello k=2 è una circonferenza di raggio k che si ottiene quando
$$ x^2 + y^2 = 2 $$
Sul piano aggiungo un'altra linea di livello
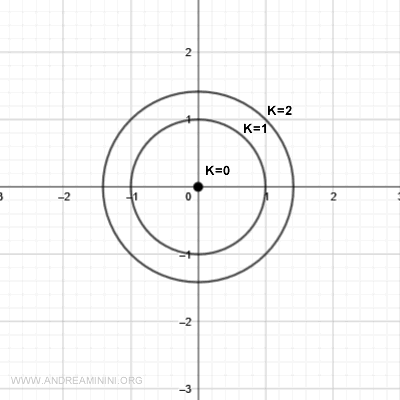
E via dicendo per k=3, k=4, ecc.
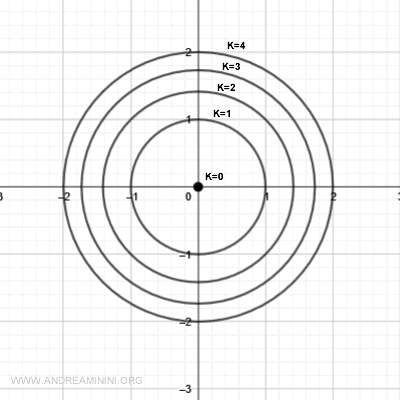
Nota. In questo caso le linee di livello diventano sempre più ravvicinate man man che incremento l'altezza. Quando l'incremento è lo stesso e la distanza tra le linee di livello si riduce, vuol dire che la pendenza del grafico aumenta.
Esempio 2
Questa funzione è leggermente più complessa.
z=f(x,y) = xy
E' un insieme di punti ottenuto quando
$$ \{ \ (x,y) \ \in R^2 \ | \ xy = k \ \} $$
In questo caso il grafico della funzione è un po' difficile da disegnare a mano
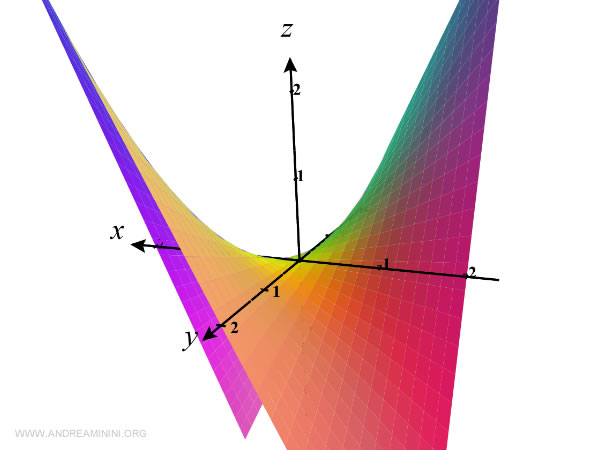
Per rappresentare più facilmente il grafico uso le linee di livello a diverse altezze (z>0) e profondità (z<0).
La linea di livello k=0 è l'insieme di punti che soddisfano l'equazione
$$ f(x,y) = x \cdot y = 0 $$
La linea di livello k=0 coincide con gli assi cartesiani delle ascisse e delle ordinate.
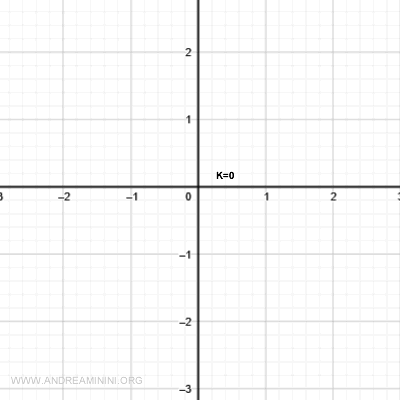
Le linee di livello k > 0 sono iperboli equilatere nel 1 e 3 quadrante (altezza)
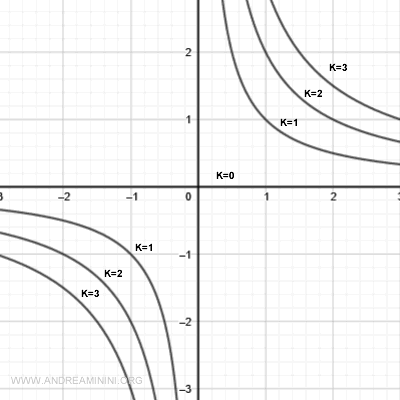
Le linee di livello k < 0 sono iperboli equilatere nel 2 e 4 quadrante (profondità)
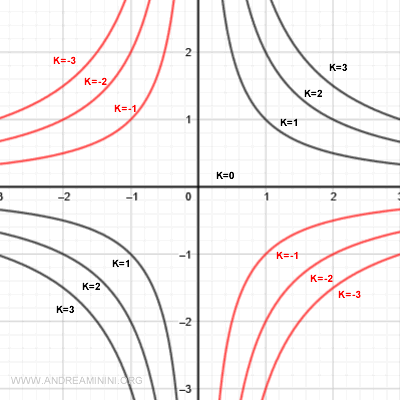
Le linee di livello delle altezze e delle profondità sono disegnate sul piano di base ed è facile confondersi.
Per distinguerle a ogni linea di livello associo un'etichetta per indicare il livello k.
Nota. Quando i livelli sono molti è meglio disegnare le linee con un colore diverso e aggiungere una legenda al grafico.
Le linee di livello e il gradiente
Il gradiente è sempre perpendicolare (ortogonale) alla linea di livello nel punto in cui viene calcolato, è diretto verso la direzione di massima crescita della funzione e il suo modulo ne indica la rapidità di variazione.
Le linee di livello di una funzione \( f(x, y) \) sono le curve nel piano \( xy \) lungo le quali la funzione assume lo stesso valore.
\[ \text{Linea di livello di quota } c: \quad f(x, y) = c \]
Più le linee sono vicine, più rapidamente varia la funzione in quella zona.
Il gradiente di una funzione scalare \( f(x, y) \) è, invece, un vettore che punta nella direzione della massima crescita della funzione. È definito dalle derivate parziali della funzione.
\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]
Il gradiente è sempre perpendicolare (ortogonale) alla linea di livello nel punto in cui è calcolato, è orientato verso il punto di massima crescita della funzione e la sua lunghezza indica la rapidità con cui la funzione cresce.
Esempio
Riprendo le linee di livello della funzione $ f(x,y) = xy $ che ho calcolato nell'esercizio precedente.

Negli assi cartesiani la funzione assume il valore k=0.
In questi punti il gradiente è ortogonale agli assi e punta verso la direzione di crescita della funzione, ossia verso i quadranti I e III del diagramma cartesiano.
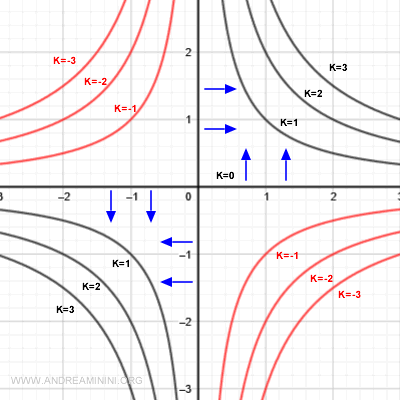
Anche nelle linee di livello in cui k=1 o k=2, dove la funzione cresce, il gradiente è ortogonale alle linee di livello e punta nella direzione della crescita della funzione.
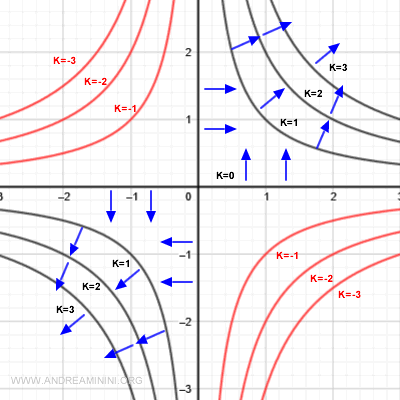
Nelle linee di livello in cui k=-1 o k=-2 la funzione assume valori negativi. Queste linee di livello (rosse) indicano una direzione in cui la funzione decresce.
Anche in questo caso il gradiente è perpendicolare e punta verso la direzione della crescita.
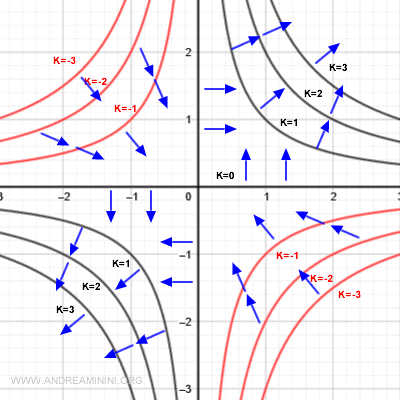
Percorrere una successione di punti che attraversano le linee di livello equivale a seguire un cammino lungo il quale la funzione varia: la velocità e la direzione di questa variazione sono descritte dal gradiente.
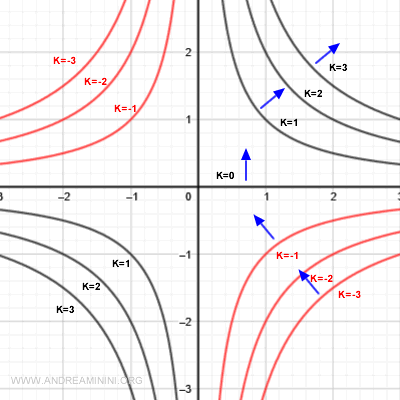
E così via.
