La funzione caratteristica
Nella teoria degli insiemi la funzione caratteristica ( o funzione indicatrice ) di un sottoinsieme A dell'insieme X è una funzione $$ 2_A : X \rightarrow \{ 0,1 \} $$ dove $$ \begin{cases} 2_A=1 \:\: se \:\: x∈A \\ 2_A=0 \:\: se \:\: x∉A \end{cases} $$
Un esempio pratico
L'insieme X è composto dai seguenti elementi
$$ X = \{ 1, 2, 3, 4, 5, 6, 7 \} $$
Il sottoinsieme A è composto dagli elementi
$$ A = \{ 4, 5, 6 \} $$
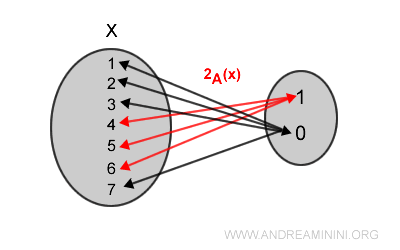
La funzione 2A è la seguente:
$$ 2_A:1 \rightarrow 0 \\ 2_A:2 \rightarrow 0 \\ 2_A:3 \rightarrow 0 \\ 2_A:4 \rightarrow 1 \\ 2_A:5 \rightarrow 1 \\ 2_A:6 \rightarrow 1 \\ 2_A:7 \rightarrow 0 $$
Questa è la funzione caratteristica del sottoinsieme A.
Quindi, la funzione inversa della funzione caratteristica individua gli elementi del sottoinsieme A.
$$ 2_A^{-1}(1) = \{ 4,5,6 \} $$
Quindi, sia X un insieme e sia 2:={0,1} esiste una corrispondenza biunivoca tra l'insieme delle parti P(X) e l'insieme 2X di tutte le funzioni da X a {0,1}
E così via.
