Funzioni di due o più variabili

Cosa sono le funzioni di più variabili

Le funzioni di due o più variabili sono funzioni con due o più variabili indipendenti. $$ f:R^n \rightarrow R $$

La funzione può restituire un solo valore (R) ma anche una coppia (R²) o una tupla di (R^m) di valori in uscita.

$$ f:R^n \rightarrow R^m $$

Esempi pratici

Esempio 1

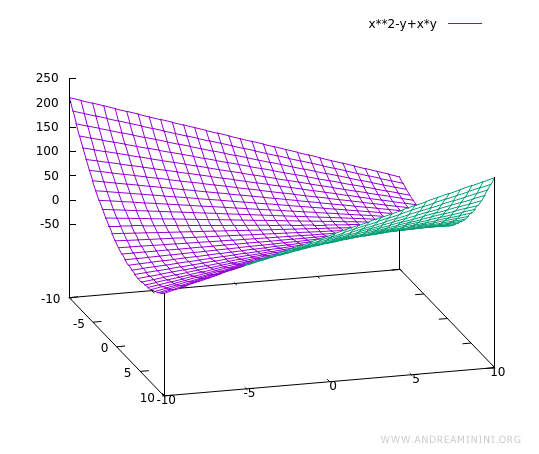
Una funzione di due variabili reali

$$ f:R^2 \rightarrow R $$

è la seguente

$$ f(x,y) = x^2 - y + xy $$

Nota. In alternativa, le variabili indipendenti posso anche indicarle come le componenti x₁ e x₂ di un vettore x. $$ f(x_1,x_2) = x_1^2 - x_2 + x_1 x_2 $$

Ecco il grafico della funzione nello spazio a tre dimensioni x, y, f(x,y)

Esempio 2

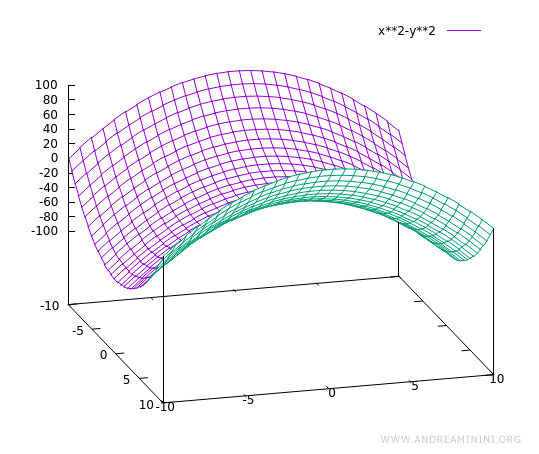
Un'altra funzione di due variabili reali

$$ f:R^2 \rightarrow R $$

è la seguente

$$ f(x,y) = x^2- y^2 $$

Ecco il grafico della funzione nello spazio a tre dimensioni x, y, f(x,y)

Esempio 3

Una funzione di tre variabili reali

$$ f:R^3 \rightarrow R $$

è la seguente

$$ f(x,y,z) = x^2 + z^2 + yz $$

Nota. Non occorre che l'espressione della funzione contenga tutte le variabili indipendenti. Ad esempio, la seguente è comunque una funzione di tre variabile anche se utilizza solo due variabili (x,y) delle tre variabili definite nella funzione (x,y,z). $$ f(x,y,z) = x^2 + y^2 $$

In questo caso il grafico non è disegnabile perché la funzione si trova in uno spazio a quattro dimensioni x, y, z, f(x,y,z).

Il grafico della funzione a due variabili

Il grafico di una funzione a due variabili f:A→R con A⊆R² è l'insieme dei punti (x,y,z) tali che (x,y) appartengono al dominio D_f della funzione mentre z al codominio.

$$ grafico \ = \ \{ (x,y,z) \in R^3 \ | \ (x,y) \in D_f \ , \ z=f(x,y) \} $$

Dove R³ è il prodotto cartesiano R³=RxRxR delle tre variabili x, y, z.

Nota. Mentre il grafico di una funzione a una variabile è una linea nel piano $$ grafico \ = \ \{ (x,y) \in R^2 \ | \ x \in D_f \ , \ z=f(x) \} $$ il grafico di una funzione di due variabili z=f(x,y) è una superficie nello spazio. $$ grafico \ = \ \{ (x,y,z) \in R^3 \ | \ (x,y) \in D_f \ , \ z=f(x,y) \} $$

In generale il grafico di una funzione a n variabili è un insieme di punti di Rⁿ⁺¹ tale che

$$ grafico \ = \ \{ (\vec{x},y) \in R^{n+1} \ | \ \vec{x} \in D_f \ , \ y=f( \vec{x} ) \} $$

Dove x è un vettore con n componenti mentre y è un numero.

$$ \vec{x} = (x_1, x_2, ... , x_n) $$

Nota. Quest'ultima notazione è molto simile a quella di una funzione a una variabile y=f(x) dove la x è però un numero reale. $$ grafico \ = \ \{ (x,y) \in R^2 \ | \ x \in D_f \ , \ z=f(x) \} $$ In una funzione a più variabili la x, invece, è un vettore di n componenti. $$ grafico \ = \ \{ (\vec{x},y) \in R^{n+1} \ | \ \vec{x} \in D_f \ , \ y=f( \vec{x} ) \} $$

E così via.