La funzione uniformemente continua
Una funzione è uniformemente continua nell'intervallo [a,b] di R se per ogni ε>0 esiste un δ=δ(ε)>0 tale che $$ |x-x'|<δ \Rightarrow |f(x)-f(x')|<ε $$ per ogni x,x' di [a,b]
Dal punto di vista geometrico vuol dire che una funzione continua in [a,b] non può mai impennarsi.
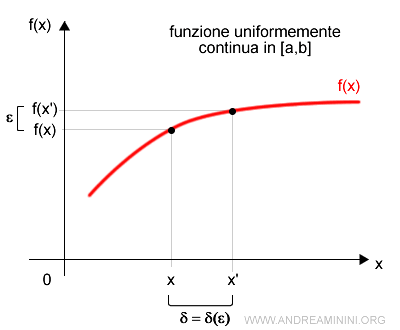
A valori più piccoli di ε corrispondono valori più piccoli di δ. E viceversa.
Questo accade perché δ è sia in funzione di x0 e di ε.
$$ δ = δ(ε, x_0) $$
Nel caso delle funzioni continue, invece, δ è sia in funzione soltanto di x0.
Nota. Il parametro ε determina il parametro δ. Pertanto, ε x δ forma un rettangolo con centro x. Per qualsiasi x dell'intervallo [a,b] la funzione uniformemente continua interseca il rettangolo ε x δ sempre ai lati verticali. Non interseca mai la base.
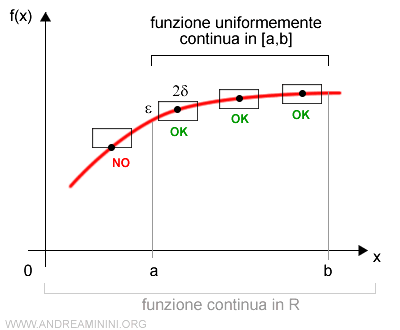
Ad esempio se δ=2ε il grafico della funzione interseca i rettangoli ai lati verticali nell'intervallo [a,b]. Pertanto, in questo intervallo la funzione è uniformemente continua. Nell'intervallo [0,a] è invece soltanto una funzione continua. Come si può vedere, il grafico interseca il primo rettangolo alla base.
Un esempio pratico
La funzione f(x)=x3 è una funzione continua in R
$$ f(x)=x^3 $$
E' anche uniformemente continua in [0,1]
Fisso un valore ε>0.
$$ ε>0 $$
Se la funzione è uniformemente continua deve esistere un valore δ>0 dipendente da ε tale che per qualsiasi x1,x2 ∈ [0,1]
$$ |x_1-x_2|<δ \rightarrow |f(x_1)-f(x_2)|<ε $$
Considerando la funzione f(x)=x3
$$ |x_1-x_2|<δ \rightarrow |x_1^3-x_2^3|<ε $$
La differenza tra due cubi si scompone in
$$ |x_1-x_2|<δ \rightarrow |(x_1-x_2) \cdot (x^2+x_1x_2+x_2^2)|<ε $$
$$ |x_1-x_2|<δ \rightarrow |(x_1-x_2)| \cdot |(x^2+x_1x_2+x_2^2)|<ε $$
Essendo una somma tra quantità non negative, posso calcolare il valore di ciascuna nell'intervallo [0,1]
$$ 0 \le x_1^2 \le 1 $$
$$ 0 \le x_1 x_2 \le 1 $$
$$ 0 \le x_2^2 \le 1 $$
Pertanto
$$ (x^2+x_1x_2+x_2^2) \le 3 $$
A questo punto riscrivo
$$ |x_1-x_2|<δ \rightarrow |(x_1-x_2)| \cdot |(x^2+x_1x_2+x_2^2)|<ε $$
$$ |x_1-x_2|<δ \rightarrow |(x_1-x_2)| \cdot 3 <ε $$
$$ |x_1-x_2|<δ \rightarrow |(x_1-x_2)| < \frac{ε}{3} $$
Pertanto, per qualsiasi valore ε esiste un valore δ
$$ δ \le | \frac{ε}{3} | $$
tale che per qualsiasi coppia di punti x1,x2 nell'intervallo [0,1] che soddisfano la condizione |x1-x2|<δ risulta
$$ |x_1-x_2|<δ \rightarrow |f(x_1)-f(x_2)| < ε $$
La differenza tra funzione continua e uniformemente continua
I due concetti sono differenti
- Una funzione uniformemente continua è sempre una funzione continua in \([a,b]\). Tuttavia, nel caso delle funzioni uniformemente continue, \(\delta = \delta(\epsilon)\) è determinato solo in funzione di \(\epsilon\) e non dipende da un punto specifico \(x_0\).
- Una funzione continua in \([a,b]\) non è detto che sia anche una funzione uniformemente continua. In questo caso, \(\delta = \delta(\epsilon, x_0)\) è determinato in funzione sia di \(\epsilon\) che di \(x_0\).
Pertanto, la condizione di uniforme continuità è più rigida rispetto alla condizione di continuità.
Nota. Per dirla diversamente, la continuità è una condizione necessaria ma non sufficiente per l'uniforme continuità.
E così via.
