Le funzioni numeriche
Una funzione è detta funzione numerica quando gli insiemi di partenza e di arrivo sono numerici.
La legge che esprime la funzione è detta espressione analitica della funzione.
Ad esempio
$$ y = f(x) = 2x+1 $$
L'espressione analitica della funzione f(x) è y=2x+1
In questo caso si tratta di una funzione a una variabile.
- La variabile y è detta variabile dipendente perché il valore che può assumere "dipende" dai valori della variabile x.
- La variabile x è detta variabile indipendente perché il valore che può assumere "non dipende" da altre variabili.
L'insieme dei valori numerici che può assumere la variabile indipendente (x) è detto campo di esistenza, dominio o dominio naturale della funzione.
Viceversa, l'insieme dei valori numerici della variabile dipendente (y) è detto codominio della funzione.
Un esempio pratico
Considero la funzione
$$ y = \frac{x+1}{x} $$
Il dominio della funzione è l'insieme dei numeri reali senza il numero zero
$$ D_f = R - \{ 0 \} $$
Lo zero non fa parte del dominio della funzione perché la funzione non è definita per x=0, in quanto lo zero al denominatore causa una divisione per zero ossia un'operazione impossibile.
La variabile indipendente può assumere valori reali nell'intervallo (-∞,0)∪(0,∞)
Per rappresentare la funzione costruisco il grafico cartesiano della funzione.
Compilo una tabella in cui associo alcuni valori della x a corrispondenti valori della y. Ogni riga della tabella è una coppia ordinata (x;y)
$$ \begin{array}{c|c} x & y \\ \hline -3 & 0,66 \\ -2 & 0,5 \\ -1 & 0 \\ 0,5 & -1 \\ 0 & ind \\ 0,5 & 3 \\ 1 & 2 \\ 2 & 1,5 \\ 3 & 1,33 \end{array} $$
Poi disegno il diagramma cartesiano ponendo il dominio (x) sull'asse orizzontale delle ascisse e il codominio (y) sull'asse verticale delle ordinate.
Fisso un verso e un'unità di misura per ogni asse.
Il punto di intersezione degli assi è detto origine O e corrisponde alla coppia ordinata (0;0)
A questo punto, aggiungo sul piano cartesiano i punti delle coppie ordinate (x;y) della tabella precedente.
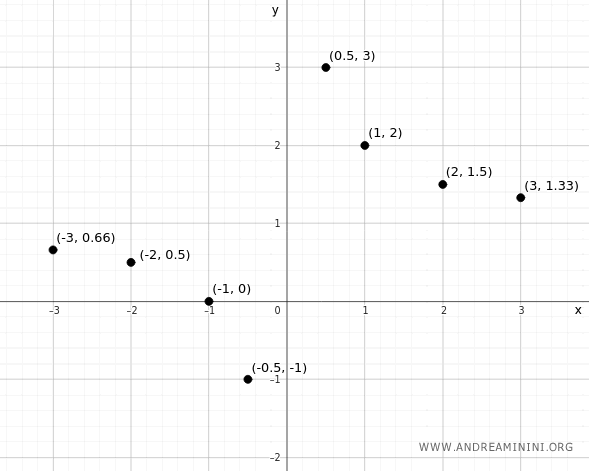
L'insieme di tutti i punti che rappresentano le coppie ordinate (x;y) compongono il grafico della funzione.
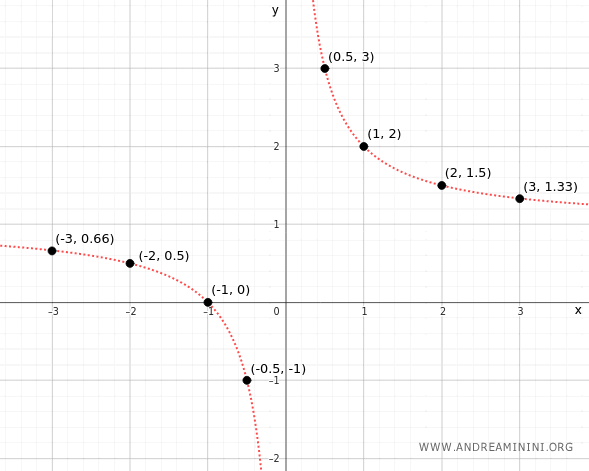
E così via.
