Punti isolati

Sia \( x_0 \) un numero reale appartenente a un sottoinsieme \( A \subset \mathbb{R} \). Si dice che \( x_0 \) è un punto isolato di \( A \) se esiste almeno un intorno di \( x_0 \) che non contiene altri elementi di \( A \) diversi da \( x_0 \) stesso.

In forma concettuale: attorno a \( x_0 \) posso ritagliare un intervallo sufficientemente piccolo che intercetta l’insieme \( A \) solo nel punto \( x_0 \).

Un intorno di \( x_0 \) è un intervallo aperto del tipo

\[ I = (x_0 - r,\; x_0 + r) \]

Dove \( r > 0 \) è un numero reale positivo.

Il punto \( x_0 \) è isolato se posso scegliere almeno un valore di \( r \) tale che

\[ I \cap A = \{x_0\} \]

Non è necessario che tutti gli intorni abbiano questa proprietà: ne basta uno solo.

Un esempio pratico

Considero l’insieme A composto da una successione di numeri razionali

\[ A = \left\{ 0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \dots , \frac{n}{n+1} \right\} \]

Dove \( n \) è un numero naturale qualsiasi.

Rappresento l’insieme sulla retta reale e osservo il punto \( 0 \).

È possibile determinare un intorno di \( 0 \) che non contiene altri elementi di \( A \), ad esempio \(  \left(-\frac{1}{3}, \frac{1}{3}\right) \)

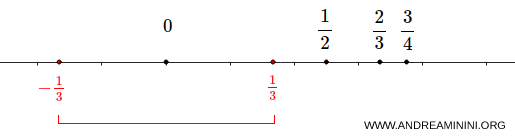
Pertanto 0 è un punto isolato dell'insieme A.

Con lo stesso ragionamento, usando intorni più piccoli, posso dimostrare che tutti gli elementi dell’insieme \( A \) sono punti isolati.

Note

Alcune osservazioni e note a margine sui punti isolati

• Insiemi finiti
  Se un insieme contiene un numero finito di punti, allora tutti i suoi punti sono isolati. Ad esempio \[ B = \{-1,\; 0,\; \tfrac{3}{5},\; 6\} \] L’insieme è formato da quattro punti distinti. Per ciascuno di questi posso costruire un intorno sufficientemente piccolo che non contenga gli altri.
• Insiemi infiniti formati da punti isolati
  Un insieme può essere infinito e tuttavia costituito esclusivamente da punti isolati. Ad esempio, l'insieme dei numeri naturali è infinito e ogni numero naturale è un punto isolato \[ \mathbb{N} = \{0,1,2,3,\dots\} \] Per ogni numero naturale \( n \) mi basta considerare un intorno di raggio \( \tfrac{1}{2} \) che non contiene altri numeri naturali.  \[ (n-\tfrac{1}{2},\; n+\tfrac{1}{2}) \] Di conseguenza, tutti i numeri naturali sono punti isolati.
• Un punto isolato non è mai un punto di accumulazione
  Intorno ad esso esiste sempre una regione in cui l’insieme non presenta altri elementi. Questa distinzione è fondamentale nello studio dei limiti delle funzioni e della struttura locale degli insiemi della retta reale.

 E così via.