Le funzioni biunivoche

Cos'è una funzione biunivoca

Una funzione f(x) è detta funzione biunivoca (o biettiva) se è iniettiva e suriettiva.

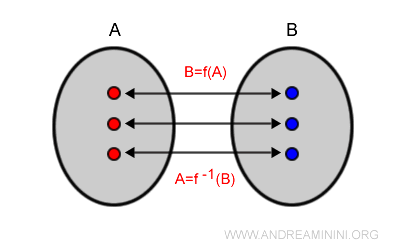
Ogni elemento dell'insieme di dominio è collegato con un elemento dell'insieme di codominio, e viceversa.

$$ f:A \leftrightarrow B $$

Vuol dire che

• A ogni valore x∈A corrisponde uno e un solo valore y∈B
• A ogni valore y∈B corrisponde uno e un solo valore x∈A

Nota. In una funzione biettiva ogni elemento del dominio ha una e una sola immagine nell'insieme di arrivo e ogni immagine dell'insieme di arrivo ha una e sola controimmagine nel dominio. C'è una corrispondenza "uno a uno" tra gli elementi dell'insieme A e quelli dell'insieme B.

Una funzione biettiva è anche detta biiezione o corrispondenza biunivoca.

Un esempio pratico

Questa funzione è biettiva perché è sia iniettiva che suriettiva.

$$ f(x) = x+1 $$

A ogni elemento x corrisponde un elemento y, e viceversa.

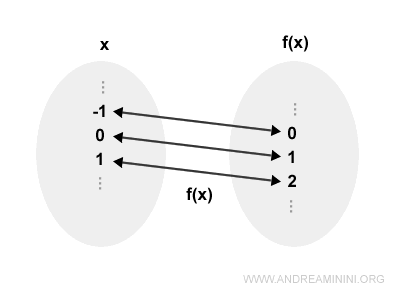
Gli elementi dell'insieme di dominio e di codominio sono in relazione biunivoca tra loro.

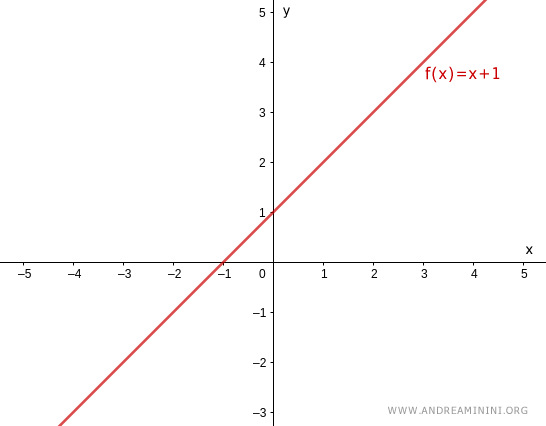
Le caratteristiche delle funzioni biettive

Le funzioni biunivoche godono delle seguenti proprietà:

• Funzione inversa
  Una funzione biunivoca è sempre invertibile. Quindi, ogni funzione biunivoca ha una funzione inversa. $$ x = f^{-1}(y) $$
• Applicazione identica
  La funzione composta di una funzione suriettiva con la sua funzione inversa è un'applicazione identica $$ x = f^{-1}(f(x)) $$

  Nota. Un'applicazione è detta identica quando f(x)=x.

Esempio

Questa funzione y=f(x) è biunivoca.

$$ y = x+1 $$

E' una funzione invertibile e la sua funzione inversa x=f-¹(y) è

$$ x = y-1 $$

La funzione composta dalla funzione invertibile e la sua inversa è un'applicazione identica

$$ x = f^{-1}(f(x)) $$

Sapendo che f(x)=x+1

$$ x = f^{-1}(y) $$

$$ x = f^{-1}(x+1) $$

Sapendo che f-¹(y)=y-1

$$ x = (x+1)-1 $$

$$ x = x $$

E così via.