Funzioni di due variabili

Cos'è una funzione di due variabili

Una funzione di due variabili fa corrispondere a una coppia di valori x,y (dominio) uno e un solo elemento z (codominio). $$ z=f(x,y) $$

Nelle funzioni reali il dominio (o campo di definizione) è un insieme di coppie ordinate di numeri reali.

$$ R^2 = [(x,y) : x,y \in R] $$

Il codominio è invece un insieme di numeri reali.

$$ f: \: R^2 \rightarrow R $$

Nota. In questo caso la x e la y sono le variabili indipendenti mentre la z è la variabile dipendente. La scelta dei nomi è comunque soggettiva. $$ f: \: (x,y) \rightarrow z $$

Come rappresentare una funzione a due variabili

La rappresentazione nello spazio tridimensionale

Per rappresentare graficamente una funzione a due variabili utilizzo un diagramma cartesiano con tre assi: x,y,z.

Si tratta di un diagramma nello spazio a tre dimensioni.

Il piano (x,y) è il prodotto cartesiano dei numeri reali R² ossia RxR.

Pertanto, il dominio della funzione a due variabili è un sottoinsieme del piano (x,y).

A ciascuna coppia (x,y) del dominio associo un valore sull'asse z=f(x,y).

Pertanto, il codominio della funzione a due variabili è un punto nello spazio a tre dimensioni.

Nota. A ogni valore della funzione a due variabili è associato un punto in uno spazio a tre dimensioni alle coordinate (x,y,z).

La rappresentazione sul piano

Posso anche rappresentare una funzione z=f(x,y) sul piano a due dimensione, mettendo in relazione le variabili a coppia (x,z) e (y,z).

In questo caso occorrono due grafici.

Quest'ultima rappresentazione è utile per mettere in evidenza le relazioni tra le singole variabili indipendenti e la variabile dipendente.

Nota. La variabile indipendente esclusa viene proiettata sul piano delle restanti variabili tramite una proiezione ortogonale.

Come costruire il grafico di una funzione di due variabili

Il metodo migliore è il metodo per punti, quello usato anche dai computer.

1. Costruisco urn reticolato di punti sul piano Oxy delle varabili indipendenti della funzione f(x,y)
2. Calcolo la quota z=f(x,y) di ciascun punto del reticolato
3. Congiungo con una linea i punti adiacenti tra loro

Il risultato finale è la rappresentazione della superficie nello spazio

Esempio

Considero la funzione

$$ z= f(x,y) = \frac{3}{x+y+1} $$

Costruisco un reticolato di punti sul piano Oxy della varabili indipendenti.

Ad esempio, la superficie del piano che ha per vertici i punti (0,0) a (3,3)

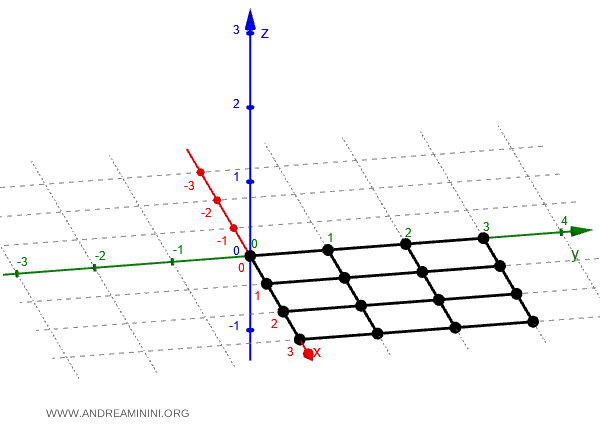
Calcolo la quota $ z $ di ciascun punto.

x	y	z = 3 / (x + y + 1)
0	0	3.0
0	1	1.5
0	2	1.0
0	3	0.75
1	0	1.5
1	1	1.0
1	2	0.75
1	3	0.6
2	0	1.0
2	1	0.75
2	2	0.6
2	3	0.5
3	0	0.75
3	1	0.6
3	2	0.5
3	3	0.4

Poi traccio una retta parallela all'asse $ z $ di pari lunghezza alla quota per ciascun punto (x,y) e unisco i punti adiacenti con una linea.

 

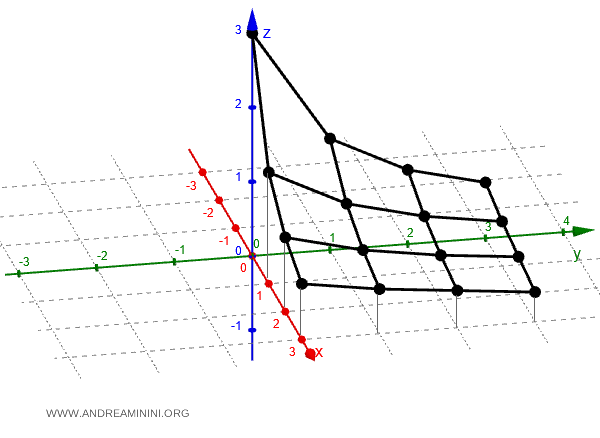
In questo modo ottengo la superficie della funzione $ f(x,y) $

Un esempio pratico

Ecco un esempio di funzione a due variabili

$$ z= f(x,y) = x^2-y^2 $$

La rappresentazione grafica della funzione nel riferimento cartesiano tridimensionale è la seguente.

Questa figura è detta parabolide iperbolico.

Per rappresentare la funzione sul piano metto a zero prima la variabile x.

$$ z= f(0,y) = -y^2 $$

Poi metto a zero la variabile y.

$$ z= f(x,0) = x^2 $$

In questo modo ottengo la proiezione della funzione sul piano (y,z) e (x,y).

E così via.