La funzione inversa
Cos'è una funzione inversa
Data una funzione y=f(x) la funzione inversa f-1 è una funzione che collega ogni elemento del codominio Y a un elemento del dominio X.
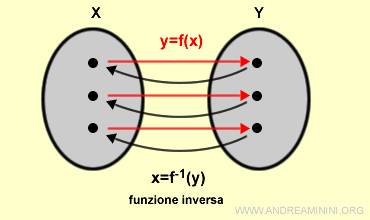
Sono dette funzioni invertibili le funzioni di X in Y che hanno anche una funzione inversa di Y in X.
Se f è una funzione biettiva di X in Y.
$$ f:X \rightarrow Y $$
La sua funzione inversa f-1 è una funzione biettiva di Y in X che a ogni elemento y∈Y associa un elemento x∈X tale che y=f(x).
$$ f^{-1}:Y \rightarrow X $$
Nota. Dove il simbolo f-1 indica che si tratta della funzione inversa di f. Non vuol dire 1/f
Non tutte le funzioni hanno però una funzione inversa.
Quelle che hanno una funzione inversa sono dette funzioni invertibili.
Sono funzioni invertibili tutte le funzioni biettive (biunivoche), ossia le funzioni che sono iniettive e suriettive.
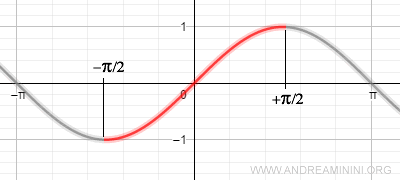
Nota. Alcune funzioni non invertibili nel proprio dominio potrebbero essere invertibili in un intervallo di valori della x. In questi casi per calcolare la funzione inversa devo ridurre la funzione in un intervallo. Ad esempio, la funzione seno non è biettiva e quindi non è invertibile nell'intero dominio. La funzione seno è però biettiva e invertibile se è ridotta nell'intervallo (-π/2;π/2). La funzione inversa della funzione seno ridotta nell'intervallo (-π/2;π/2) è l'arcoseno.
Un esempio pratico
Esempio 1
Ho la funzione f(x)=x+1 e due insiemi X e Y
$$ X=\{ 1,2,3 \} $$
$$ Y=\{ 2,3,4 \} $$
La funzione f è una relazione che genera il sottoinsieme R del prodotto cartesiano XY
$$ R = \{ (1,2),(2,3),(3,4) \} $$
In pratica la relazione collega ogni elemento del primo insieme con un elemento del secondo insieme
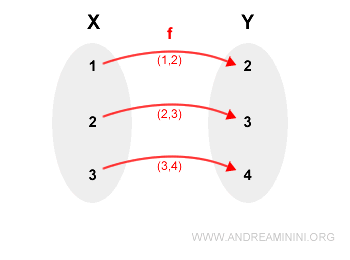
Nota. La relazione f è anche una funzione perché il primo elemento compare una sola volta nelle coppie ordinate.
La relazione inversa R-1 è la seguente:
$$ R^{-1} = \{ (2,1),(3,2),(4,3) \} $$
Anche la relazione inversa è una funzione perché il primo elemento delle coppie appare una sola volta.
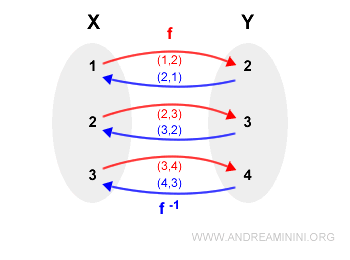
Pertanto, f-1 è la funzione inversa di f.
La funzione f è invece detta funzione invertibile perché ha una funzione inversa.
Esempio 2
Dati due insiemi X e Y
$$ X=\{ -1,0,1 \} $$
$$ Y=\{ -1,0,1 \} $$
La relazione y=x2 genera un insieme di coppie ordinate
$$ R = \{ (-1,1),(0,0),(1,1) \} $$
Questa relazione è anche una funzione perché ogni primo elemento delle coppie ordinate appare una sola volta.
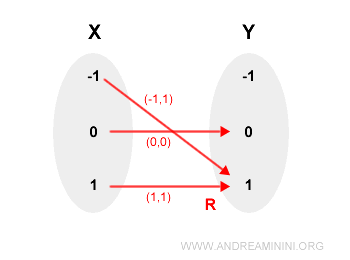
La relazione inversa R-1, invece, non è una funzione.
$$ R^{-1} = \{ (1,-1),(0,0),(1,1) \} $$
Il motivo è molto semplice, l'elemento 1 appare due volte come primo elemento delle coppie ordinate.
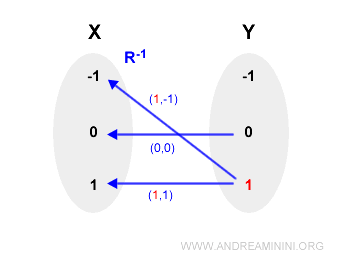
In conclusione, la relazione inversa della funzione f(x)=x2 non è a sua volta una funzione.
La funzione f(x)=x2 nel dominio finito {-1,0,1} non è invertibile.
Esempio 3
Considero la funzione y=2x-1
$$ y = 2x - 1 $$
E' una funzione biiettiva e quindi è invertibile.
Per ricavare la funzione inversa esplicito la x in funzione di tutto il resto
$$ 2x = y + 1 $$
$$ x = \frac{y+1}{2} $$
Nella funzione inversa y è la variabile indipendente e x è la variabile dipendente.
Se rappresentassi la funzione invertibile e la funzione inversa sul piano cartesiano i due grafici si sovrapporrebbero.
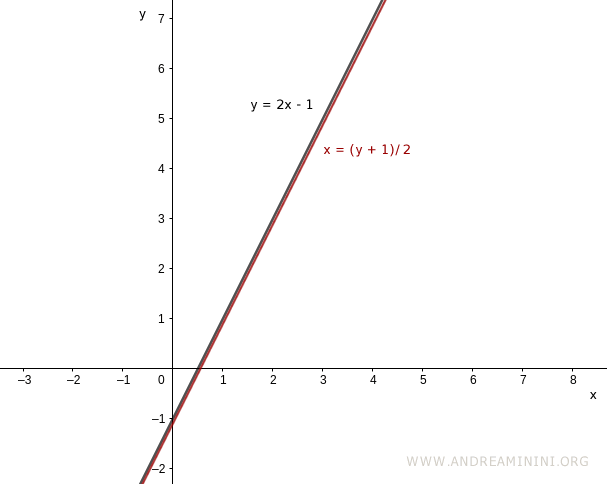
Per poter rappresentare la funzione inversa nello stesso piano cartesiano devo scambiare x e y tra loro
$$ y = \frac{x+1}{2} $$
In questo modo posso rappresentare entrambe le funzioni sullo stesso diagramma cartesiano
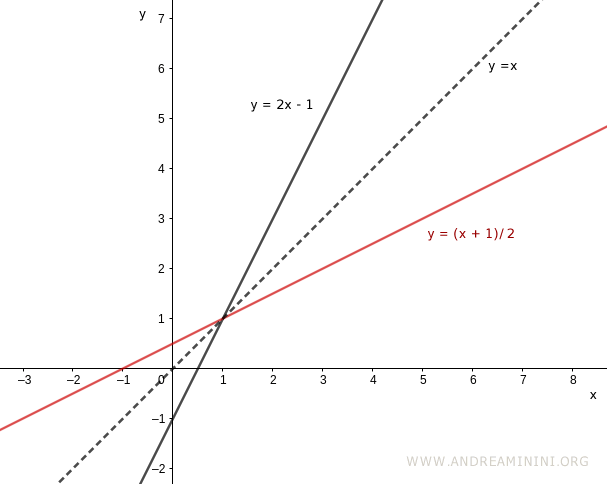
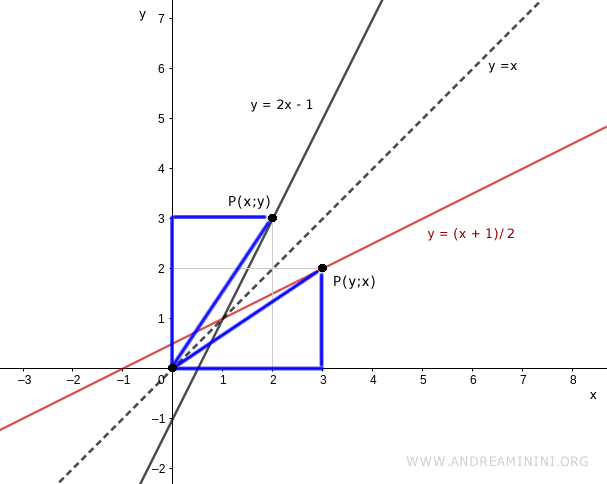
Il grafico della funzione y=2x-1 e della funzione inversa x=(y+1)/2 con le variabili x⇔y sostituite tra loro sono simmetrici sul piano cartesiano rispetto alla bisettrice del I e del III quadrante.
Nota. Se un punto P(x;y) appartiene al grafico della funzione invertibile, allora il punto P(y;x) appartiene al grafico della funzione inversa. E viceversa. Questo accade perché i due grafici sono sempre simmetrici rispetto alla bisettrice.

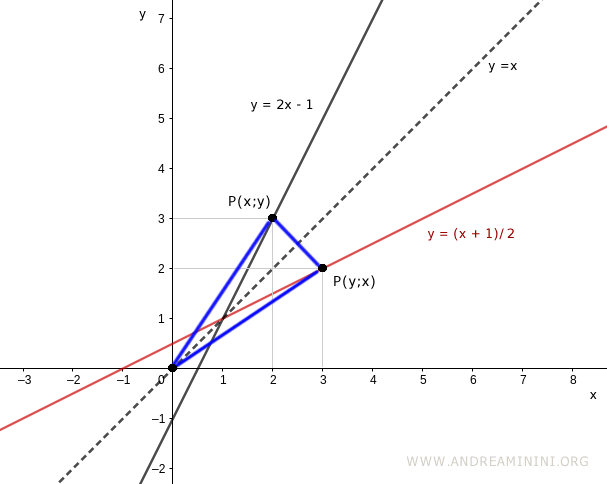
Se unisco i punti con l'origine e le rispettive proiezioni sugli assi si formano due triangoli rettangolo congruenti tra loro. E' un'altra caratteristica delle funzioni inverse.
Essendo congruenti si forma anche un terzo triangolo isoscele unendo i due punti tra loro con l'origine.
Esempio 4
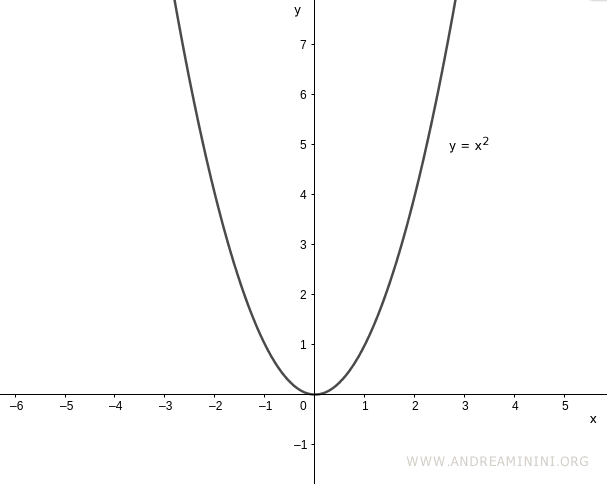
La funzione y=x2 è definita nell'insieme dei numeri reali (R)
$$ y=x^2 \ \ \ \forall x \in R $$
Questa funzione non è biettiva, quindi non è invertibile nel suo dominio (R).
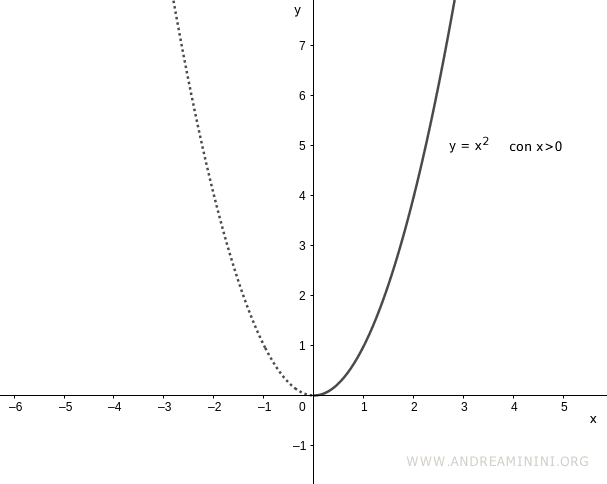
Tuttavia, se opero una restrizione del dominio ai soli numeri reali positivi R+ la funzione diventa biettiva.
$$ y=x^2 \ \ \ \forall x \in R + $$
Quindi, nell'intervallo (0,∞) la funzione y=x2 è invertibile.
Per ricavare la sua funzione inversa, calcolo la radice quadrata in entrambi i membri ed esplicito la x
$$ \sqrt{y}=\sqrt{x^2} $$
$$ x = \sqrt{y} $$
Per rappresentare la funzione inversa sullo stesso diagramma cartesiano opero una sostituzione di variabile x e y
$$ y = \sqrt{x} $$
Le due funzioni sono simmetriche rispetto alla bisettrice del I e del III quadrante.
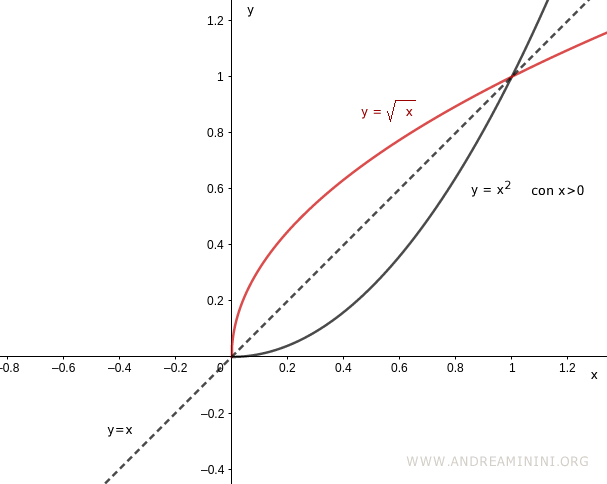
Nota. Questo dimostra che una funzione non invertibile nel suo dominio potrebbe esserlo dopo una restrizione del dominio in un intervallo.
Le funzioni biettive sono invertibili
Se una funzione f di X in Y è una funzione biettiva, allora la f è anche una funzione invertibile.
Una funzione è biettiva ( biunivoca ) se è sia iniettiva che suriettiva.
- Iniettiva. Per ogni elemento X (dominio) esiste un elemento distinto di Y.
- Suriettiva. Per ogni elemento di Y (codominio) esiste almeno un elemento di X.
Dimostrazione
Se la funzione y=f(x) è biettiva allora
$$ dominio(f)=codominio(f^{-1})=X $$
$$ codominio(f) = dominio(f^{-1})=Y $$
Ipotizzo di avere due coppie ordinate con lo stesso elemento nel codominio
$$ (x_1, y) \\ (x_2 , y ) $$
La funzione è iniettiva, quindi x1 e x2 devono essere necessariamente uguali.
$$ x_1 = x_2 $$
D'altra parte la funzione è anche suriettiva, per ogni elemento y deve essere uno e un solo elemento x.
$$ (x,y) $$
In questo caso la controimmagine di y è x.
$$ x = f^{-1}(y) $$
Ho così dimostrato che una funzione biettiva è anche una funzione invertibile.
Le proprietà delle funzioni inverse
Le principali proprietà delle funzioni inverse sono le seguenti
- Se f-1 è la funzione inversa di f, allora f è la funzione inversa f-1.
- Se f-1[f(x)]=x, allora f[f-1(y)]=y
- Se y=f(x) e x=f-1(y) allora f e f-1 sono proposizioni equivalenti
Come trovare una funzione inversa
Per disegnare il grafico della funzione inversa f-1(x) di una funzione invertibile f(x) posso seguire due metodi grafici e un metodo analitico.
Metodo 1
Disegno il grafico di una funzione invertibile f(x) sul piano cartesiano.
Ad esempio y=log x
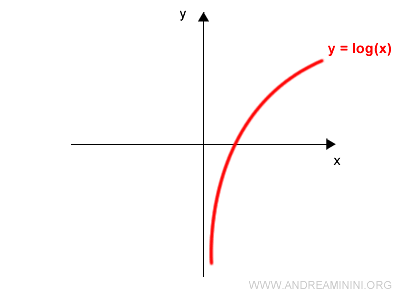
Nel grafico traccio la bisettrice del I e III quadrante che ha per equazione y=x.
E' una retta passante per l'origine con angolo di 45°.
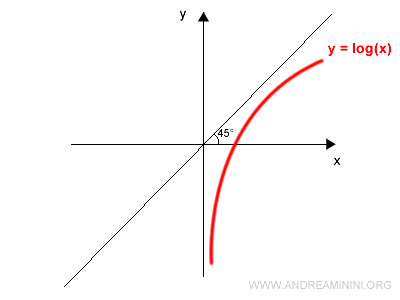
Poi disegno il grafico simmetrico della funzione f(x) rispetto alla bisettrice.
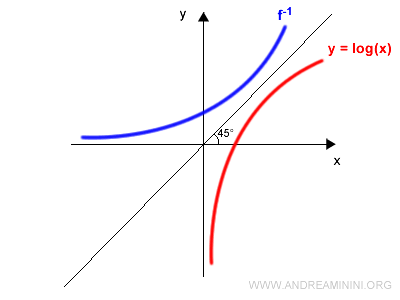
Ora elimino la funzione f(x).
Infine indico y sull'asse delle ascisse e x sull'asse delle ordinate.
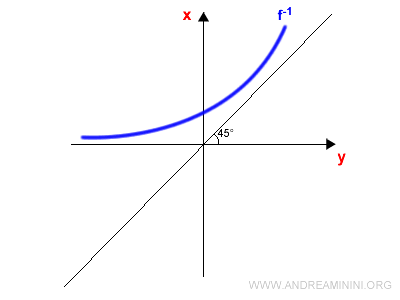
Ho così ottenuto il grafico della funzione inversa f-1(x).
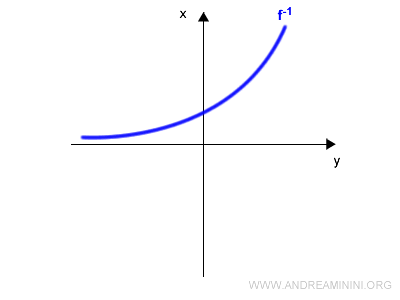
Metodo 2
Disegno il grafico di una funzione invertibile f(x) sul piano cartesiano.
Ad esempio y=log x

Ruoto il piano cartesiano di 90° ruotando l'asse y verso sinistra e l'asse x verso l'alto.
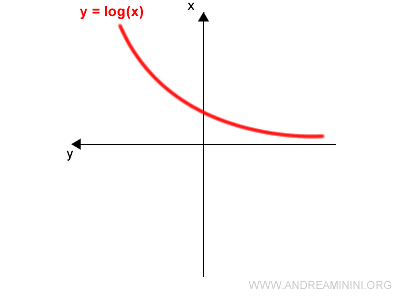
Poi ruoto il piano cartesiano di 180° sull'asse verticale.
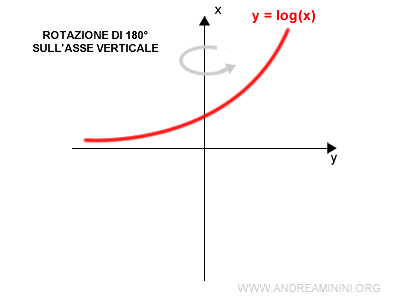
Nota. Quest'ultima operazione si può immaginare anche in un altro modo. E' come se guardassi il grafico allo specchio. Nello specchio il grafico viene riflesso rispetto all'asse verticale. Il risultato finale è lo stesso.
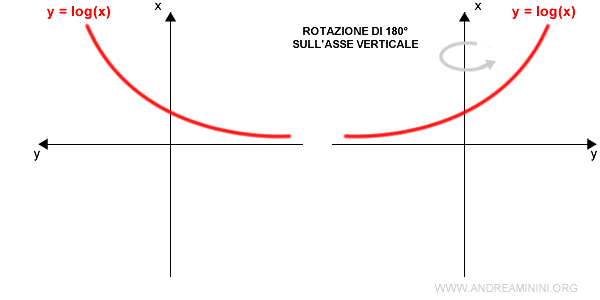
In questo modo ottengo il grafico della funzione inversa f-1(x).
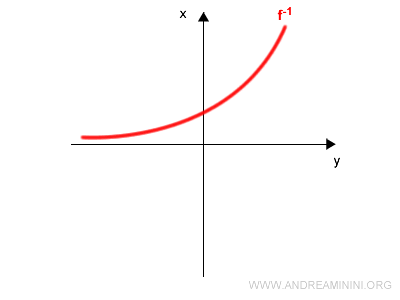
Metodo 3 (analitico)
Per trovare analiticamente la funzione inversa di una funzione invertibile y=f(x) basta mettere in evidenza la x rispetto alla y.
Prendo come esempio la funzione invertibile y=log x
$$ y = \log x $$
Il grafico della funzione logaritmica è il seguente

Devo cercare di mettere in evidenza la x rispetto alla y.
Metto l'esponenziale a potenza in entrambi i membri dell'equazione.
$$ e^y = e^ { \log x } $$
Nota. Quest'ultima equazione è equivalente alla precedente perché ho effettuato la stessa operazione algebrica sia al membro di sinistra che al membro di destra..
L'esponenziale elevato per il logaritmo è uguale all'argomento del logaritmo ossia elog x = x.
$$ e^y = e^ { \log x } $$
$$ e^y = x $$
Ora la variabile x è in funzione della variabile y.
Ho così trovato la funzione inversa della y=log x.
$$ x = e^y $$
Dal punto di vista grafico la funzione inversa x=ey appare in questo modo.
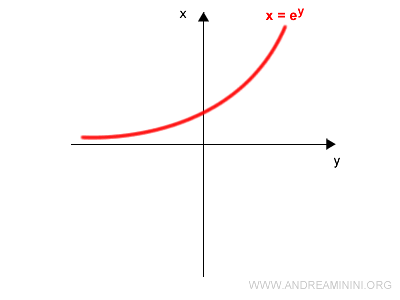
Nota. E' lo stesso risultato ottenuto con il metodo grafico in un altro esempio di questa pagina.
E così via.
