Intorno di un punto

Un intorno di un punto \( x_0 \) è un insieme di punti sufficientemente vicini a \( x_0 \).

Dove \( \delta \) è un numero reale positivo arbitrario, scelto come parametro per determinare l’ampiezza dell’intorno.

Generalmente, l’intorno di un punto \( x_0 \) è un insieme di punti $ I_0 $ che non include né il punto \( x_0 \) né gli estremi.

È però necessario distinguere tra due tipi di intorno.

• Intorno (o intorno puntato)
  E' un intorno di $ x_0 $ con $ \delta > 0 $ che non contiene $ x_0 $ $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$
• Intorno completo
  E' un intorno di $ x_0 $ con $ \delta> 0 $ che contiene anche $ x_0 $ $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0 + \delta)  $$ Si può anche scrivere $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid  x- \delta < x_0 < x + \delta \} $$ oppure $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid |x-x_0| < \delta \} $$

Nota. Quando in analisi matematica si parla semplicemente di intorno di \( x_0 \), senza specificare nulla, si intende quasi sempre l’intorno che esclude il punto \( x_0 \), perché ciò che conta è il comportamento della funzione in prossimità del punto e non il valore assunto nel punto stesso. Questa distinzione è fondamentale nello studio dei limiti e della continuità.

Un esempio pratico

Se il punto x₀ è dieci

$$ x_0 = 10 $$

Fissato un delta uguale a due

$$ δ=2 $$

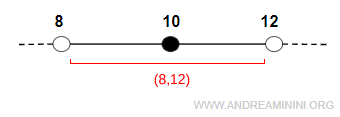
L'intorno completo di $ x_0 $ è un intervallo compreso tra otto e dodici

$$ I_0 = (x_0-δ, x_0+δ) $$

$$ I_0 = (10-2, 10+2) $$

$$ I_0 = (8, 12) $$

Si tratta di un intervallo aperto a cui appartengono tutti i numeri reali maggiori di otto e minori di dodici. Poiché ho specificato che si tratta di un intorno "completo", il punto $ x_0 = 10 $ è compreso nell'intorno.

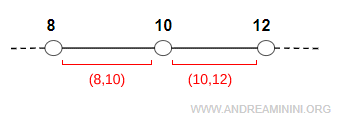
Viceversa, l'intorno di $ 10 $ (intorno puntato) non contiene il punto \( x_0 = 10 \) e non è un intervallo aperto, ma l’unione di due intervalli aperti disgiunti:

$$ I_0 = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$

$$ I_0 = (10 - 2, 10)\ \cup\ (10, 10 + 2) $$

$$ I_0 = (8, 10)\ \cup\ (10, 12) $$

In questo caso il punto $ x_0 = 10 $ non fa parte dell'intorno.

Nota. Il punto $ x_0 $ appartiene all'interno se non specificato diversamente. Può essere centrale o meno rispetto agli estremi dell'intervallo. Può anche essere un estremo dell'intervallo. Ad esempio, posso definire un intorno usando come estremi due numeri reali positivi diversi tra loro $ \delta_1 \ne \delta_2 $  $$ (x_0-δ_1, x_0+δ_2) $$ In questo caso il ll punto $ x_0 $ non è più il punto medio dell'intorno. In alcuni testi si parla di intorno circolare in $ \mathbb{R} $ quando $ \delta_1 = \delta_2 $. Tuttavia, lo stesso termine viene usato per identificare una zona del piano in $ \mathbb{R}^2 $. Quindi, per evitare di confondere le idee, io userò il termine generico "intorno" o "intorno completo" per indicare qualsiasi intorno di un punto su una retta, mentre intorno circolare per indicare l'intorno di un punto sul piano.

Intorno destro e intorno sinistro

A volte è utile studiare il comportamento di una funzione considerando soltanto i punti che si trovano a destra oppure a sinistra di un punto assegnato.

In questi casi si parla di intorno destro e di intorno sinistro.

• Intorno destro
  L’intorno destro di un punto \( x_0 \), indicato con \( I_0^+ \), è l’insieme dei punti reali maggiori di \( x_0 \) e compresi nell'intervallo aperto $ ( x_0, x_0+ \delta ) $ con \( \delta > 0 \). $$ I_0^+ = (x_0, x_0 + \delta) $$
• Intorno sinistro
  L’intorno sinistro di un punto \( x_0 \), indicato con \( I_0^- \), è l’insieme dei punti reali minori di \( x_0 \) e compresi nell'intervallo aperto $ ( x_0- \delta, x_0 ) $ con \( \delta > 0 \). $$ I_0^- = (x_0 - \delta, x_0) $$

Questi due concetti sono fondamentali nello studio dei limiti destro e sinistro e della continuità di una funzione.

Ad esempio, se \( x_0 = 2 \) e \( \delta = 0{,}5 \), allora l’intorno destro è \[ I_0^+ = (2, 2.5) \] mentre l'intorno sinistro è \[ I_0^- = (1.5, 2) \]

Intorno di infinito

Altre volte è utile studiare l’insieme dei punti appartenenti a un intervallo aperto illimitato superiormente oppure inferiormente.

In questi casi si parla di intorno di infinito.

• Intorno di meno infinito
  L’intorno di meno infinito è l’intervallo aperto e illimitato inferiormente costituito da tutti i punti minori di un numero reale \( a \), preso come estremo.  \[ I(-\infty) = (-\infty, a) = \{ x \in \mathbb{R} \mid x < a \} \]
• Intorno di più infinito
  L’intorno di più infinito è l’intervallo aperto e illimitato superiormente costituito da tutti i punti maggiori di un numero reale \( a \), preso come estremo. \[ I(+\infty) = (a, +\infty) = \{ x \in \mathbb{R} \mid x > a \} \]

Quando si utilizza il simbolo di infinito, è sempre necessario indicare esplicitamente il segno più o meno, perché il simbolo generico \( \infty \) viene usato sia per indicare \( -\infty \) sia per indicare \( +\infty \).

Ad esempio, se scelgo \( a = 3 \) come estremo, allora  un intorno di meno infinito è \[  I(-\infty) = (-\infty, 3) \] mentre un intorno di più infinito è \[ I(+\infty) = (3, +\infty) \] In questo caso, per fare un esempio numerico, il numero \( -1000 \) appartiene all’intorno di meno infinito, mentre il numero \( 10 \) appartiene all’intorno di più infinito.

Note

Alcune note e osservazioni personali sugli intorni

• L'intersezione e l'unione di due intorni di $ x_0 $ è ancora un intorno di $ x_0 $

E così via.