Teorema di Heine Cantor
Una funzione f(x) continua nell'intervallo chiuso e limitato [a,b] è uniformemente continua in [a,b].
Il teorema di Heine-Cantor introduce una condizione sufficiente per l'uniforme continuità di una funzione.
Una funzione continua non è detto che sia anche uniformemente continua.
Tuttavia, se la funzione continua si analizza in un intervallo chiuso e limitato, la funzione è anche uniformemente continua.
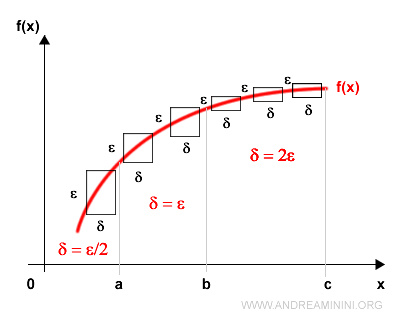
Spiegazione. In un intervallo [a,b] si cerca una relazione δ=δ(ε) tale da soddisfare le condizioni di uniforme continuità. Questa relazione sarà valida soltanto nell'intervallo [a,b]. In altri intervalli occorre definire un'altra relazione δ=δ'(ε). L'unica condizione necessaria è che la funzione sia continua nell'intervallo considerato. Ad esempio, nel grafico precedente la funzione è uniformemente continua in [b,c] con la relazione δ=2ε. Nell'intervallo [a,b] è uniformemente continua con la relazione δ=ε. Infine, nell'intervallo [0,a] è soltanto continua rispetto alla relazione δ=ε/2. In quest'ultimo intervallo [0,a] non si può trovare una relazione di uniforme continuità perché la curva tende a inclinarsi verticalmente nell'intorno destro di zero. In questo caso, secondo il teorema di Heine-Cantor, per trovare la relazione di uniforme continuità dovrei considerare un intervallo più piccolo, ad esempio nell'intervallo [0.5, a] nell'intorno sinistro del punto a, dove la funzione è uniformemente continua con la relazione δ=ε/3.
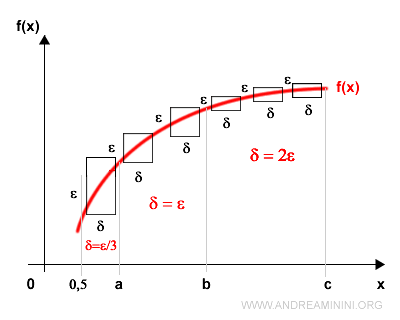
Viceversa, nell'intervallo [0,0.5] la funzione è continua ma non uniformemente continua. E via dicendo.
Dimostrazione
Per dimostrare il teorema di Heine-Cantor parto da un'ipotesi assurda.
Affermo che esiste un ε0>0 tale che, per qualunque δ>0, esistono dei valori x,x' dipendenti da δ tali che
$$ \exists ε_0>0: \forall δ>0, \exists x,x' \in [a,b] \Rightarrow |x-x'|<δ, |f(x)-f(x')| \ge ε_0 $$
E' la negazione della tesi di uniforme continuità di una funzione.
Nota. Secondo la definizione di uniforme continuità di una funzione vale invece la seguente affermazione $$ \forall ε>0: \exists δ>0: \forall x,x' \in [a,b], |x-x'|<δ \:\: \Rightarrow \:\: |f(x)-f(x')| \le ε $$
Sostituisco δ con 1/n dove n è un numero naturale n∈N.
$$ \exists ε_0>0: \forall n \in N, \exists x_n,x'_n \in [a,b] \Rightarrow |x_n-x'_n|< \frac{1}{n} , |f(x_n)-f(x'_n)| \ge ε_0 $$
Secondo il teorema di Bolzano-Weierstrass esiste una successione xk
$$ x_{n_k} - \frac{1}{n_k} < x'_{n_k} < x_{n_k} + \frac{1}{n_k} $$
che converge verso un punto x0 nell'intervallo [a,b]
Per il teorema dei due carabinieri anche x'nk converge a x0 per k tendente a infinito
$$ \lim_{k \rightarrow ∞} x'_{n_k} = x_0 $$
Essendo la funzione f(x) una funzione continua in [a,b], dati due punti qualsiasi x,x'
$$ \lim_{k \rightarrow ∞} [f(x_{n_k})-f(x'_{n_k})] = f(x_0) - f(x_0) = 0 $$
Quindi
$$ x_0 = 0 $$
Questo però contrasta con l'ipotesi iniziale secondo cui x0≥ε
$$ |f(x)-f(x')| \ge ε_0 $$
In questo modo ho dimostrato per assurdo la validità del teorema di Heine-Cantor.
E così via.
