Intervalli numerici
In matematica un intervallo è un insieme di numeri contigui delimitato da un estremo inferiore (a) e/o un estremo superiore (b) con a< b.
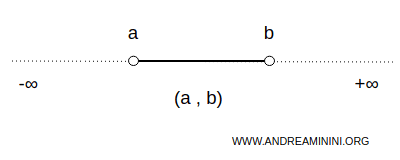
Un intervallo è chiuso se include gli estremi, è aperto se non comprende gli estremi.
Può essere limitato tra due estremi oppure illimitato.
La differenza tra gli estremi indica l'ampiezza dell'intervallo.
$$ b - a $$
Il centro dell'intervallo è il punto:
$$ \frac{a+b}{2} $$
mentre il raggio dell'intervallo è la metà dell'ampiezza:
$$ \frac{b-a}{2} $$
Nota. Nella notazione matematica convenzionale, un intervallo tra due estremi "a" e "b" si rappresenta con la virgola, come in (a,b). Tuttavia, dato che in Italia la virgola è frequentemente utilizzata per indicare il punto decimale, in alcuni contesti si può trovare il punto e virgola come separatore, cioè (a;b). Ad esempio, se i due estremi sono numeri decimali, 2,5 e 3,4, separarli con una virgola renderebbe l'intervallo poco comprensibile (2,5,3,4). In questi casi sarebbe meglio usare il punto decimale (2.5,3.4) oppure usare il punto e virgola come separatore (2.5;3.4).
La differenza tra intervallo limitato e illimitato
Gli intervalli possono essere limitati o illimitati
- Intervallo limitato
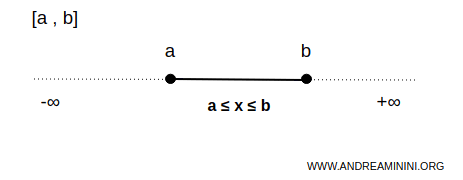
Un intervallo limitato è un insieme di numeri compresi tra due numeri, un estremo inferiore (a) e un estremo superiore (b), con a< b.
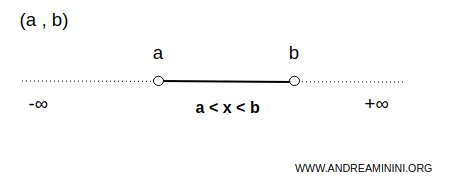
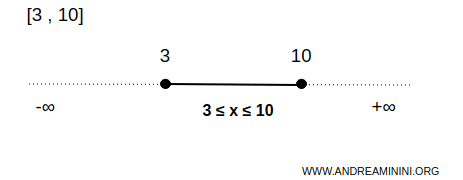
Esempio. L'insieme dei numeri reali compreso tra 3 e 10 è un intervallo limitato di numeri reali. Dove 3 è l'estremo inferiore e 10 è l'estremo superiore. $$ \forall \ x \in (3,10) \Rightarrow \forall \ x \in R \ | \ 3 \lt x \ \lt 10 $$
- Intervallo illimitato
Un intervallo illimitato è un insieme di numeri che seguono o precedono un numero reale x. Può essere illimitato superiormente (illimitato a destra) oppure illimitato inferiormente (illimitato a sinistra)
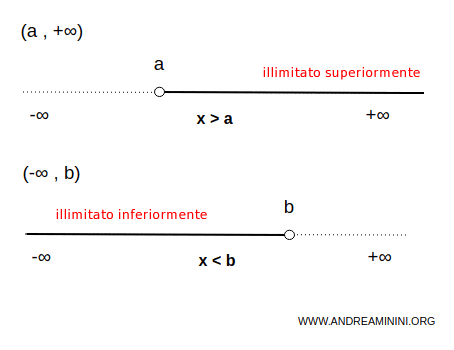
I simboli $ - \infty $ (meno infinito) e $ + \infty $ (più infinito) non sono numeri e quindi vanno sempre esclusi dall'intervallo.
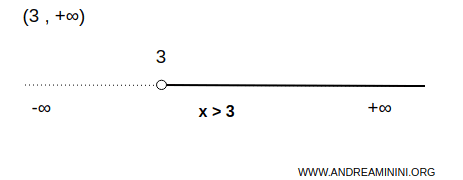
Esempio. L'insieme dei numeri reali maggiori di 3 è un intervallo illimitato superiormente (illimitato a destra) e limitato inferiormente (limitato a sinistra). Dove 3 è l'estremo inferiore mentre manca l'estremo superiore. $$ \forall \ x \in (3,+\infty) \Rightarrow \forall \ x \in R \ | \ x \ \gt 3 $$
Esempio. L'insieme dei numeri reali minori di 3 è un intervallo illimitato inferiormente (illimitato a sinistra) e limitato superiormente (limitato a destra). Dove 3 è l'estremo superiore mentre manca l'estremo inferiore. $$ \forall \ x \in (-\infty,3) \Rightarrow \forall \ x \in R \ | \ x \ \lt 3 $$
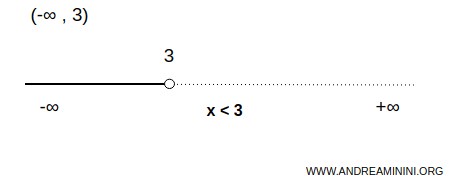
Il caso dell'intervallo illimitato inferiormente e superiormente
Quando l'intervallo è illimitato sia inferiormente che superiormente, l'intervallo comprende tutti i numeri dell'insieme numerico di riferimento.

L'intervallo illimitato inferiormente e superiormente è detto illimitato.
Pertanto, se si legge che un intervallo è illimitato senza alcuna indicazione ulteriore, si intende illimitato inferiormente e superiormente.
Esempio. L'insieme illimitato superiormente e inferiormente dei numeri reali (R) è un intervallo illimitato a sinistra e a destra che comprende tutti i numeri reali. $$ \forall \ x \in (-\infty,+\infty) \Rightarrow \forall \ x \ \in R $$
Gli intervalli chiusi e aperti
Un intervallo può essere chiuso o aperto.
- Intervallo chiuso
E' chiuso se include l'estremo. Si indica con le parentesi quadre [ ] a sinistra e/o a destra. Graficamente gli estremi aperti si indicano con un cerchio completamente nero.
Esempio. Questo intervallo limitato è chiuso $$ x \in [3,10] $$ Vuol dire che l'intervallo comprende tutti i numeri tra 3 e 10 inclusi gli estremi 3 e 10. Essendo chiusi entrambi gli estremi sono indicati con un cerchio nero.
- Intervallo aperto
E' aperto se non comprende l'estremo. Si indica con le parentesi tonde ( ) a sinistra e/o a destra. Dal punto di vista grafico gli estremi aperti si indicano con un cerchio aperto con la parte interna bianca.
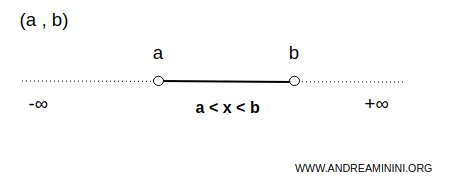
Esempio. Questo intervallo limitato è aperto $$ x \in (3,10) $$ Vuol dire che l'intervallo comprende tutti i numeri tra 3 e 10 esclusi gli estremi 3 e 10. Essendo aperti entrambi gli estremi si indicano con lo sfondo bianco.
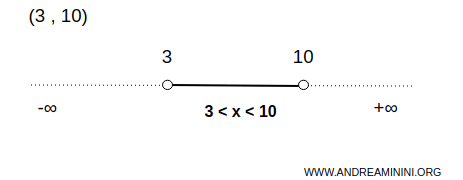
Esistono diverse combinazioni di intervalli.
Ad esempio può aperto a destra e chiuso a sinistra o viceversa. Illimitato a sinistra e chiuso a destra e via dicendo.
Nel prossimo paragrafo elenco alcuni esempi pratici.
Nota. In alcuni libri l'intervallo aperto è indicato con una notazione diversa $$ ]a,b[ \ = (a,b) $$ Il concetto è sempre lo stesso. Personalmente preferisco usare le parentesi tonde.
Esempi pratici
Esempio 1
Questo intervallo limitato è aperto a sinistra e chiuso a destra
$$ x \in (3,10] $$
Vuol dire che l'intervallo comprende tutti i numeri tra 3 e 10, escluso l'estremo inferiore 3 e incluso l'estremo superiore 10.
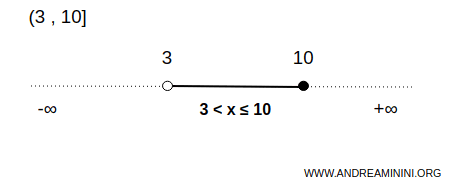
Esempio 2
Questo intervallo limitato è chiuso a sinistra e aperto a destra
$$ x \in [3,10) $$
Vuol dire che l'intervallo comprende tutti i numeri tra 3 e 10, incluso l'estremo inferiore 3 ed escluso l'estremo superiore 10.
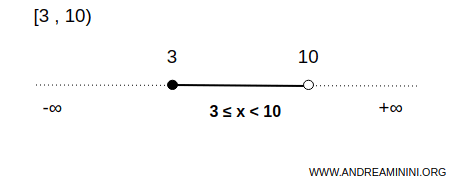
Esempio 3
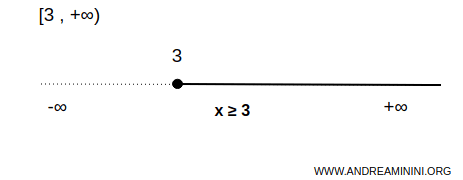
Questo intervallo illimitato superiormente è chiuso a sinistra e aperto a destra
$$ x \in [3,+\infty) \Rightarrow \forall \ x \ge 3 $$
Vuol dire che l'intervallo comprende tutti i numeri maggiori o uguali a 3, dove tre è l'estremo inferiore ed è incluso nell'intervallo. L'intervallo non ha un estremo superiore.
Nota. Quando manca l'estremo inferiore o superiore si utilizza il simbolo più o meno infinito (∞). In un intervallo l'estremo illimitato (+∞ oppure -∞) è sempre aperto perché ±∞ è solo un simbolo, non è un numero e non può essere incluso nell'intervallo. Pertanto, in un estremo illimitato si usano esclusivamente le parentesi tonde. Mai le parentesi quadre. Ecco alcuni esempi possibili (∞,a) , (a,∞) , (∞,a] , [a,∞).
Esempio 4
Questo intervallo illimitato superiormente è aperto a sinistra e a destra
$$ x \in (3,+\infty) \Rightarrow \forall \ x \gt 3 $$
Vuol dire che l'intervallo comprende tutti i numeri maggiori 3, dove tre è l'estremo inferiore e non è incluso nell'intervallo. L'intervallo non ha un estremo superiore.

Esempio 5
Questo intervallo illimitato inferiormente è aperto a sinistra e chiuso a destra
$$ x \in (-\infty,10] \Rightarrow \forall \ x \ \le 10 $$
Vuol dire che l'intervallo comprende tutti i numeri minori o uguali a 10, dove dieci è l'estremo superiore ed è incluso nell'intervallo. L'intervallo non ha un estremo inferiore.
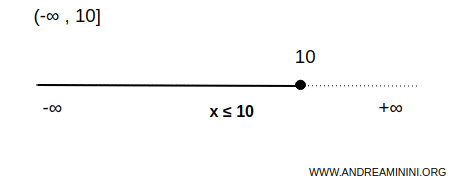
Esempio 6
Questo intervallo illimitato inferiormente è aperto a sinistra e a destra
$$ x \in (-\infty, 10) \Rightarrow \forall \ x \ \lt 10 $$
Vuol dire che l'intervallo comprende tutti i numeri minori di 10, dove dieci è l'estremo superiore e non è incluso nell'intervallo. L'intervallo non ha un estremo inferiore.
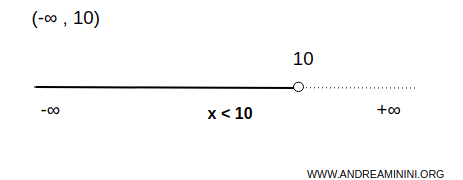
E così via.
