Le traslazioni di una funzione
La traslazione di una funzione è una trasformazione geometrica che permette di modificare la posizione di un grafico mantenendone invariata la forma.
In altre parole, una traslazione è uno spostamento "rigido" del grafico di una funzione sul piano cartesiano.
Dove il termine "rigido" significa che la forma del grafico non cambia: né la forma geometrica del grafico, né la sua curvatura.
La traslazione può avvenire in diversi modi: lungo l’asse delle ascisse (x), lungo l’asse delle ordinate (y) oppure in entrambe le direzioni contemporaneamente.
A cosa serve? Le traslazioni sono utili per visualizzare come cambia una funzione al variare dei parametri e costituiscono spesso il primo passo nello studio di trasformazioni più complesse, come dilatazioni e riflessioni. Un esempio applicativo importante è quello delle telecomunicazioni, dove le traslazioni orizzontali descrivono il ritardo temporale di un segnale
Traslazione orizzontale
Se parto da una funzione qualunque \( y = f(x) \), una traslazione orizzontale di \( a \) unità la ottengo modificando l’argomento \( x \):
- \( y = f(x - a) \) genera una traslazione verso destra di \( a \) unità.
- \( y = f(x + a) \) genera una traslazione verso sinistra di \( a \) unità.
E' utile sottolineare che per spostare il grafico della funzione in "avanti" (ossia verso destra) il segno è invertito rispetto all’intuizione: Il segno meno ( $ -a $ ) sposta la funzione in avanti, mentre il segno più ( $ +a $ ) la sposta indietro (verso sinistra).
Esempio pratico
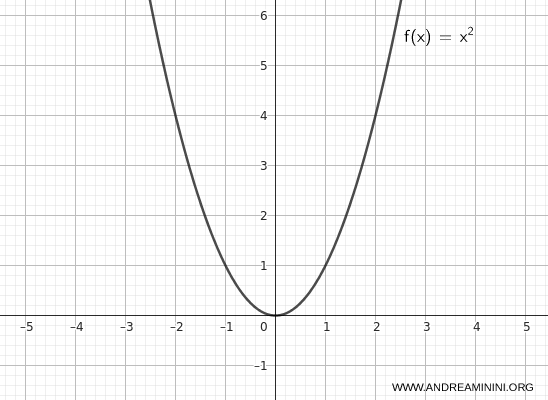
Prendo la funzione \( f(x) = x^2 \).
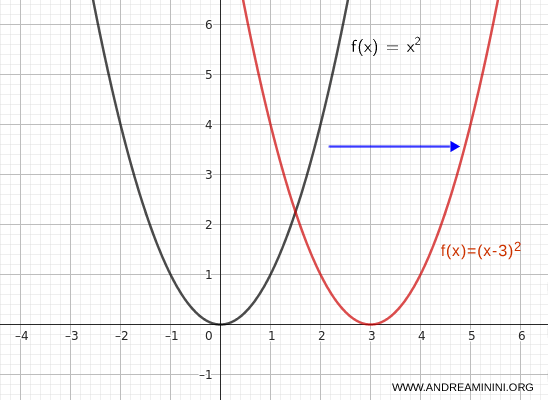
Sposto il grafico della funzione in avanti (verso destra).
$$ y = (x - 3)^2 $$
In questo caso il vertice della parabola si sposta da \( (0, 0) \) a \( (3, 0) \).
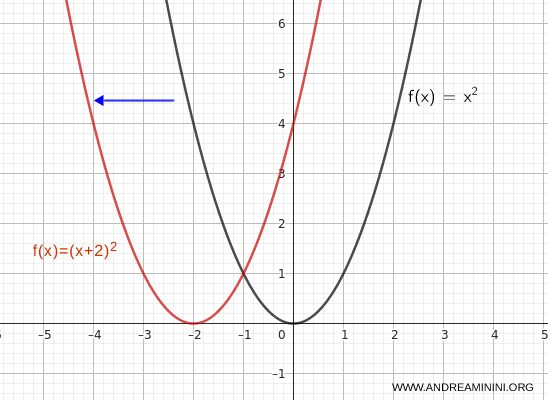
Ora sposto il grafico della funzione indietro (verso sinistra).
$$ y = (x + 2)^2 $$
In quest'altro caso il vertice si sposta da \( (0, 0) \) a \( (-2, 0) \)
Traslazione verticale
Se parto da una funzione \( y = f(x) \), una traslazione verticale di \( b \) unità la ottengo aggiungendo o sottraendo un termine fuori dalla funzione.
- \( y = f(x) + b \) causa una traslazione verso l’alto di \( b \) unità.
- \( y = f(x) - b \) causa una traslazione verso il basso di \( b \) unità.
Qui il segno segue l’intuizione: il segno più (+b) sposta il grafico verso l'alto, mentre il segno meno (-b) lo sposta verso il basso.
Esempio pratico
Considero la funzione dell'esempio precedente.
$$ f(x) = x^2 $$
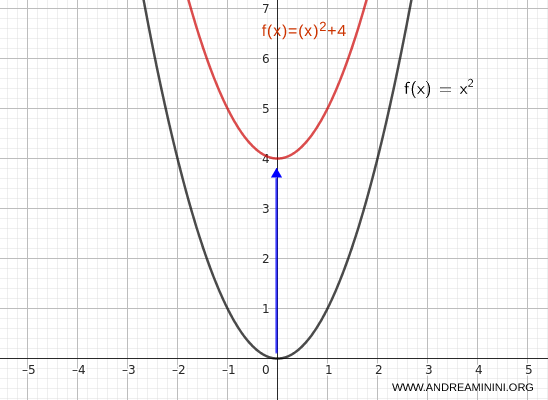
Per spostare il grafico verso l'alto di 4 unità scrivo:
$$ y = x^2 + 4 $$
In questo modo il vertice della funzione si sposta da \( (0, 0) \) a \( (0, 4) \).
Se invece volessi spostarlo in basso di una unità scriverei:
$$ y = x^2 - 1 $$
In quest'altro caso il vertice diventa \( (0, -1) \).

Traslazione obliqua
La traslazione obliqua è una trasformazione che combina la traslazione orizzontale e quella verticale.
- \( y = f(x - a) + b \) sposta il grafico di \( a \) verso destra e di \( b \) verso l’alto
- \( y = f(x + a) - b \) sposta il grafico di \( a \) verso sinistra e di \( b \) verso il basso
Esempio
Considero di nuovo la funzione
$$ f(x) = x^2 $$
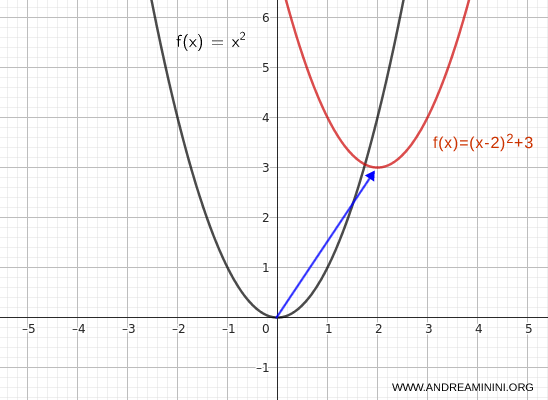
Per spostare la funzione di 2 unità in avanti e 3 in alto scrivo:
$$ y = (x - 2)^2 + 3 $$
Il vertice della funzione si sposta da \( (0,0) \) a \( (2, 3) \) tramite un'azione combinata della traslazione orizzontale e verticale.
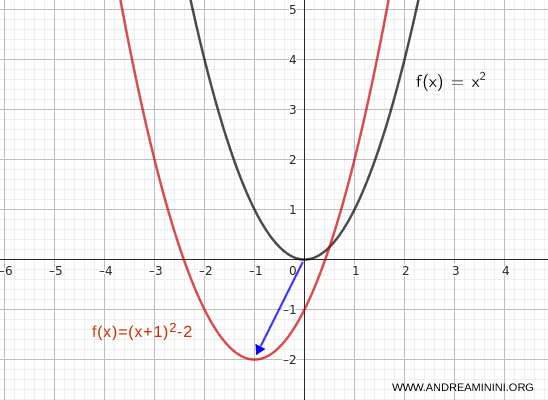
Faccio un altro esempio per spostare la funzione di una unità a sinistra (indietro) e 2 unità in basso, scrivo:
$$ y = (x + 1)^2 - 2 $$
In questo caso il vertice della funzione si sposta da \( (0,0) \) al punto \( (-1, -2) \).
E via dicendo
