La funzione identità
La funzione identità è una funzione composta da una funzione f:A→B con la sua funzione inversa f-1:B→A. $$ f^{-1} \ o \ f(x) = x $$ ossia $$ f^{-1}[f(x)] = x $$
E' detta funzione identità perché associa ogni elemento x del dominio a se stesso.
$$ f^{-1}[f(x)] = x $$
e viceversa
$$ f[f^{-1}(y)] = y $$
Questa è la rappresentazione di una funzione identità con i diagrammi di Eulero-Venn
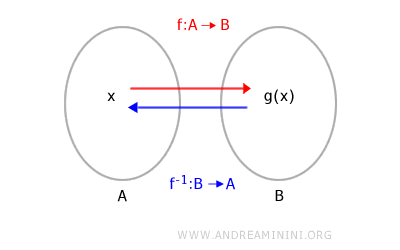
La funzione identità è detta semplice se applicata a un insieme e corrisponde a una biiezione.
Nota. Le funzioni identità sono compatibili con tutte le strutture matematiche (es. spazi vettoriali, strutture algebriche, spazi metrici, spazi topologici, ecc.). A seconda dei vari casi, la funzione identità ha caratteristiche specifiche. Ad esempio, in una struttura algebrica la funzione identità è un isomorfismo, in uno spazio lineare è una funzione lineare, in uno spazio metrico è una isometria, in uno spazio topologico è un omeomorfismo.
Un esempio pratico
Considero la funzione f(x) = x2
$$ y = x^2 $$
e la sua funzione inversa f-1 = √y
$$ x = \sqrt{y} $$
La funzione composta f-1[f(x)] delle due funzioni è x
$$ f^{-1}[ f(x)] = \sqrt{f(x)} = \sqrt{x^2} = x $$
E' detta funzione identità perché ogni elemento del dominio x è associato con se stesso.
Nota. Vale anche l'inverso f[f-1(x)] $$ f[ f^{-1}(x)] = [f^{-1}(x)]^2 = [\sqrt{x}]^2 = x $$
Esempio 2
Considero la funzione f(x) = 2x
$$ y = 2x $$
e la sua funzione inversa f-1= 1/y
$$ x = \frac{y}{2} $$
La funzione composta f-1[f(x)] delle due funzioni è x
$$ f^{-1}[ f(x)] = \frac{f(x)}{2} = \frac{2x}{2} = x $$
Nota. Vale anche l'inverso f[f-1(x)] $$ f[ f^{-1}(x)] = \frac{f^{-1}(x)}{2} = \frac{2x}{2} = x $$
Esempio 2
Considero la funzione f(x) = sin(x)
$$ y = \sin(x) $$
e la sua funzione inversa f-1= arcsin(y)
$$ x = \arcsin(y) $$
La funzione composta f-1[f(x)] delle due funzioni è x
$$ f^{-1}[ f(x)] = \arcsin[ f(x) ] = \arcsin[ \sin(x) ] = x $$
Nota. Vale anche l'inverso f[f-1(x)] $$ f[ f^{-1}(x)] = \sin [ f^{-1}(x) ] = \sin( \arcsin x) = x $$
E così via.
