Le funzioni iniettive

Cos'è una funzione iniettiva

Una funzione matematica f(x) è detta iniettiva se a ogni coppia di elementi distinti x₁ e x₂ dell'insieme di definizione (dominio) sono associate immagini distinte f(x₁) e f(x₂) nel codominio $$ se \: x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$ e se a ogni coppia di elementi uguali è associata la stessa immagine $$ se \: x_1 = x_2 \Rightarrow f(x_1) = f(x_2) $$

Utilizzando i diagrammi di Venn il concetto di iniettività diventa più chiaro.

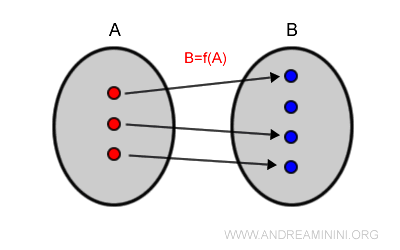
In alternativa si può dire che una funzione è iniettiva da A e B se gni elemento dell'insieme A ha un'immagine distinta nell'insieme B.

L'insieme A è il dominio della funzione matematica f(x) mentre l'insieme B è il codominio.

Nota. La definizione matematica formale di funzione iniettiva è la seguente: $$ \forall \ x_1 , x_2 \ \in D_f \ | \ x_1 \ne x_2 \Rightarrow \ f(x_1) \ne f(x_2) $$ Per ogni coppia di numeri x₁, x₂ del dominio D_f la funzione f(x), diversi tra loro x₁≠x₂, la funzione ha immagini diverse f(x₁)≠f(x₂)

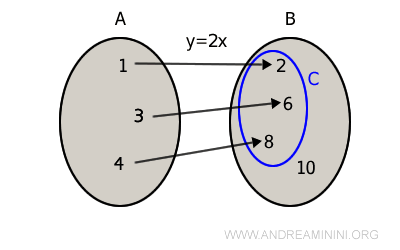
Ovviamente l'insieme di arrivo B non è detto che coincida con il codominio della funzione, perché alcuni elementi di B potrebbero non essere l'immagine di un elemento di A.

Pertanto, il codominio (C) della funzione potrebbe anche essere un sottoinsieme di B.

Un esempio pratico

Esempio 1

Questa funzione definita nell'insieme dei numeri reali R è una funzione inettiva

$$ f(x) = x+1 $$

perché per ogni x di R esiste un valore y diverso della f(x)

x	y=f(x)
x=-3	-2
x=-2	-1
x=-1	0
x=0	1
x=1	2
x=2	3
x=3	4

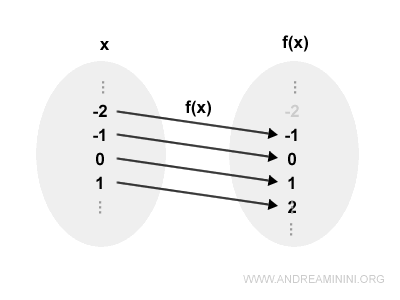
Tutti gli elementi x del dominio hanno immagini distinte y=f(x) tra loro.

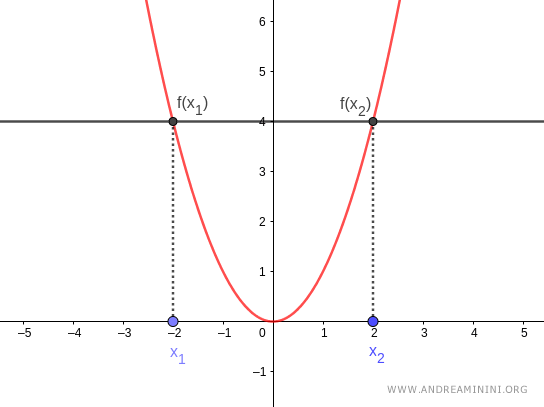
Nota. Dal punto di vista geometrico una funzione è iniettiva se ogni retta parallela all'asse dell'ascissa interseca il grafico della funzione al più in un punto. Pertanto, la retta può intersecare una sola volta oppure non intersecare affatto il grafico della funzione.

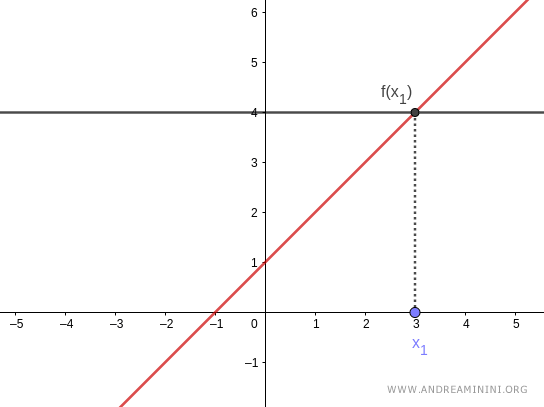
Questo equivale a dire che ogni punto (x) del dominio della funzione ha una e una sola immagine (y) nel codominio, distinta da quella di tutti gli altri punti del dominio.

Esempio 2

Questa funzione non è una funzione inettiva

$$ f(x) = x^2 $$

perché gli elementi x del dominio non hanno immagini f(x) distinte tra loro

x	y=f(x)
x=-3	9
x=-2	4
x=-1	1
x=0	0
x=1	1
x=2	4
x=3	9

Ad esempio, il valore y=4 è ottenuto sia con x=-2 che con x=+2.

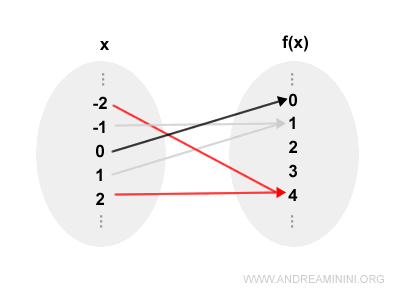
Nota. Dal punto di vista geometrico una funzione non è iniettiva se esiste una retta parallela all'asse dell'ascissa che interseca il grafico della funzione y=f(x) in più di un punto. Se questo accade vuol dire che due punti diversi x₁, x₂ del dominio hanno la stessa immagine (y).

E così via.